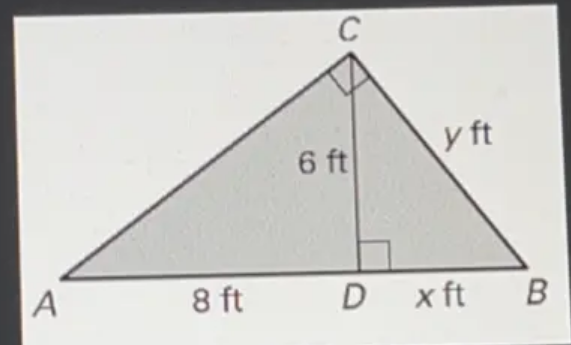
What is the value of x and y?

To find \(x\) and \(y\), we can use the Pythagorean theorem in the right triangles \(\triangle ADC\) and \(\triangle BDC\).

\(For \triangle ADC: \)

• \(AD = 8\) ft
• \(CD = 6\) ft
• Using the Pythagorean theorem:
  \[AC^ 2 = AD^ 2 + CD^ 2\]
  \[AC^ 2 = 8^ 2 + 6^ 2\]
  \[AC^ 2 = 64 + 36\]
  \[AC^ 2 = 100\]
  \[AC = \sqrt { 100} = 10 \text { ft} \]

\[For \triangle BDC: \]

• \(BD = x\) ft
• \(CD = 6\) ft
• \(BC = y\) ft (since \(\triangle ABC\) is a right triangle at \(C\))
• Using the Pythagorean theorem:
  \[BC^ 2 = BD^ 2 + CD^ 2\]
  \[y^ 2 = x^ 2 + 6^ 2\]

\[For \triangle ABC: \]

• \(AB = AD + BD= 8 + x\)
  • Using the Pythagorean theorem:
    \[AB^ 2 = BC^ 2 + AC^ 2\]
    \[( 8+ x) ^ 2 = y^ 2 + 10^ 2\]

Therefore, the values are:

• \(x = 4.5\) ft
• \(y = 7.5\) ft

Supplemental Knowledge

The Pythagorean theorem is a fundamental principle in geometry that relates the lengths of the sides of a right-angled triangle. It states that in a right-angled triangle, the square of the length of the hypotenuse (\(c\)) is equal to the sum of the squares of the lengths of the other two sides (\(a\) and \(b\)). Mathematically, it can be expressed as:
\[c^ 2 = a^ 2 + b^ 2\]

Knowledge in Action

The Pythagorean theorem can be applied in multiple real-life applications, from construction and navigation to computer graphics. When building or designing furniture or plotting gardens, using this theorem helps ensure accuracy when it comes to measuring corners accurately.

For students tackling geometry problems involving right triangles, having the right tools can make all the difference. UpStudy offers an excellent Pythagorean Theorem Calculator that simplifies these calculations for you. Whether you're working on homework or preparing for exams, this calculator will help you quickly find missing side lengths in right-angled triangles.

Explore UpStudy’s Pythagorean Theorem Calculator today and enhance your understanding and efficiency in solving geometric problems!