How to Calculate Percent Error?

What is the Percent Error

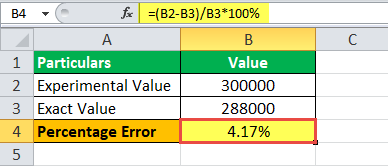
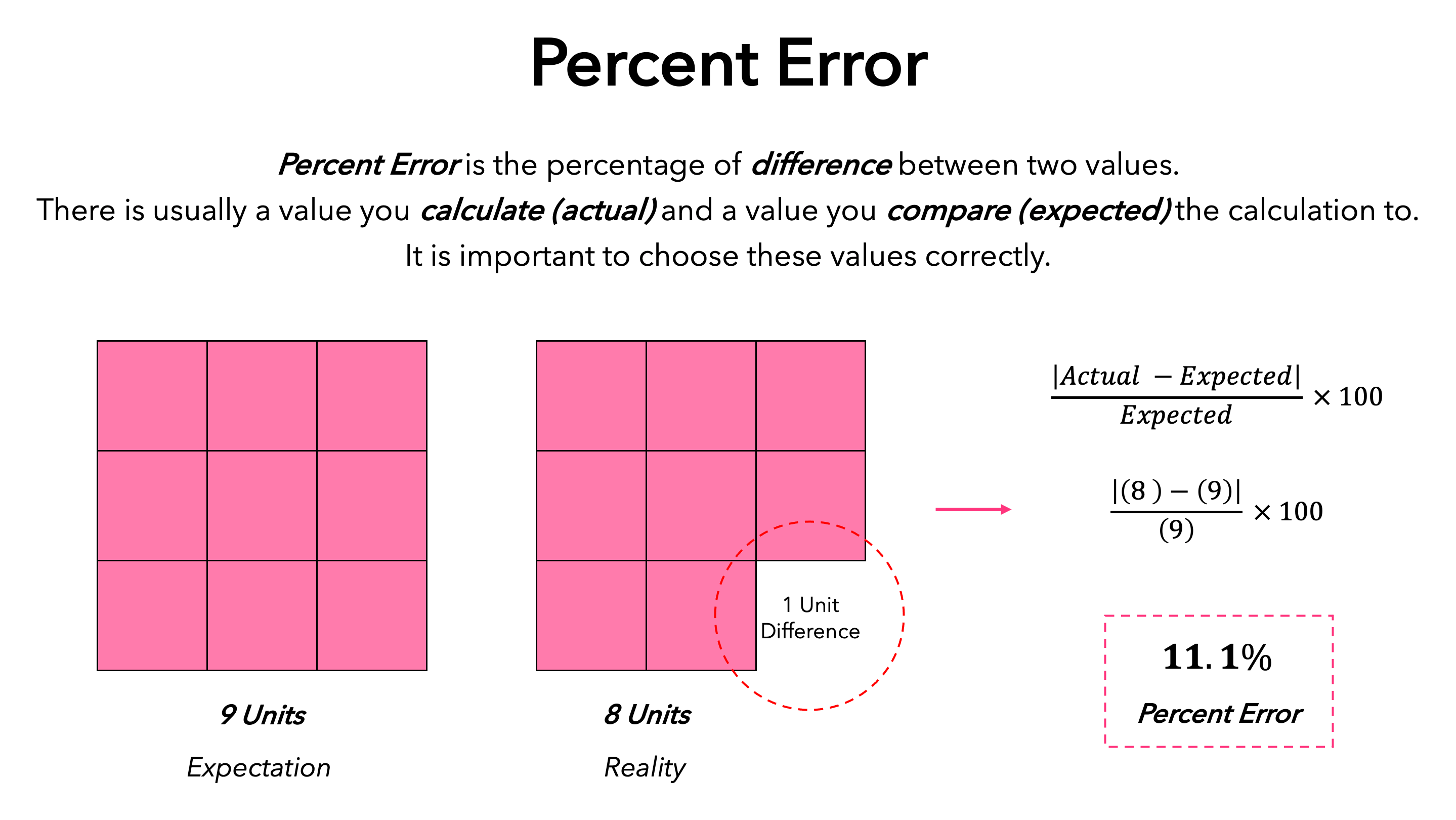
Percent error is a statistical measure that expresses differences between measured or estimated values and accepted or true values as percentages, making it especially helpful when applied in fields like science and engineering where precision is of great significance. Human error, instrument limitations and environmental influences can all contribute to errors in measurement. Knowing the percent error helps indicate both trial precision and data quality. Experiments should produce results that correspond closely with actual values; however, discrepancies often arise. Percent error provides a quantitative measure for these differences between actual values and experiment results, making analysis and improvement of measurement techniques simpler; for instance, a 5% error could represent a minor deviation, suggesting measurements were close to reality, while a 60% deviation could represent serious deviation.

The Importance of Percent Error

Percent error plays an essential role in scientific research, data analysis and quality control. Experimental science relies on it as an indispensable way of validating hypotheses; scientists often compare experimental findings against established or theoretical values during experiments conducted to verify hypotheses and calculate percent error to see how accurate results are and whether experimental methods need improvement; for instance, chemists measuring yield can use percent error as an assessment tool to ensure experimental values match theoretical yield values expected theoretical yield calculations.

Quality control processes in manufacturing use percent error to evaluate product reliability; frequent measurement errors indicate potential flaws with production that could cost businesses millions in losses. Understanding percent error also equips individuals to make more informed decisions in cooking, construction or any field that uses precise measurements; for instance if an ingredient quantity called for differs significantly from that measured amount it could significantly alter end result of dish.

Steps to Calculate Percent Error

Calculate Absolute Error

Before beginning to calculate percent error, first determine your absolute error. Absolute errors measure any variances between what was observed (or estimated) and the true (or accepted) values regardless of their directionality. The formula for absolute error is given by:

$\text{Absolute Error}=|V_{\text{true}}-V_{\text{observed}}|$

For instance, if you measure a length as 10.5 cm, but the actual length is 10 cm, the absolute error is calculated as follows:

$\text{Absolute Error}=|10-10.5|=0.5\text{ cm}$

This means that your measurement deviated from the true value by 0.5 cm.

Step 2: Calculate Relative Error

Once you have the absolute error, the next step is to calculate the relative error. This calculation compares the absolute error to the true value, providing a dimension of how significant the error is in relation to the actual value. The formula for relative error is:

$\text{Relative Error}=\frac{\text{Absolute Error}}{V_{\text{true}}}$

Using the previous example, if the actual value is 10 cm, the relative error would be:

$\text{Relative Error}=\frac{0.5}{10}=0.05$

This indicates that the measurement error is 5% of the true value.

Step 3: Calculate Percent Error

The final step is to express the relative error as a percentage. Multiply the relative error by 100 to get the percent error:

$\text{Percent Error}=\text{Relative Error}\times 100$

Continuing with the example, we find:

$\text{Percent Error}=0.05\times 100=5\%$

So, the percent error in measuring the length is 5%, indicating that the observed value deviated from the actual value by 5%.

Percent Error Formula Analysis

Basic Formula for Percent Error

The basic formula for calculating percent error can be summarized as follows:

$\text{Percent Error}=\frac{|V_{\text{actual}}-V_{\text{estimated}}|}{V_{\text{actual}}}\times 100$

This formula efficiently captures the difference between the actual and estimated values while accounting for the actual value itself. By expressing the result as a percentage, it allows for easier comparisons across different measurements.

Contextual Use of the Formula

In various scientific settings, understanding how percent error is expressed is of critical importance. Common in many fields like chemistry or physics is keeping negative values as this helps signify whether measurements consistently surpass expected values versus whether measurements consistently fall short of them, such as when measuring the yield of chemical reaction yield. If positive errors arise during chemical yield measurement procedures, positive errors could signal flaws with procedures or unaccounted reactions occurring, while negative errors act as feedback mechanisms providing essential feedback to researchers.

Real-World Case Analysis

Example 1: Laboratory Applications

Let’s consider a case in a laboratory setting where researchers measure the density of a sample of aluminum. Suppose they calculate the density to be 2.68 g/cm³ but find that the accepted value is 2.70 g/cm³. They can follow the steps outlined to calculate the percent error:

1. First, compute the absolute error:

$\text{Absolute Error}=|2.70-2.68|=0.02{\text{g/cm}}^3$

2. Next, find the relative error:

$\text{Relative Error}=\frac{0.02}{2.70}\approx 0.007407$

3. Finally, express this as a percentage:

$\text{Percent Error}=0.007407\times 100\approx 0.74\%$

This calculation indicates that their experimental density measurement was 0.74% away from the accepted value, providing a quantifiable measure of accuracy.

Example 2: Daily Life Applications

Now, consider a practical scenario in cooking where a recipe requires 300 grams of flour. However, a cook mistakenly estimates the amount to be 320 grams. Here’s how to calculate the percent error:

1. Find the absolute error:

$\text{Absolute Error}=|300-320|=20\text{grams}$

2. Calculate the relative error:

$\text{Relative Error}=\frac{20}{300}\approx 0.06667$

3. Finally, compute the percent error:

$\text{Percent Error}=0.06667\times 100\approx 6.67\%$

In this case, the cook’s measurement of flour was off by 6.67%, indicating that the additional flour could significantly alter the recipe's outcome.

Common Misunderstandings and Corrections

Misunderstandings arise frequently when it comes to calculating percent error calculations, the most frequent of which involves misinterpreting its sign: many individuals believe it should always be positive while it may be common practice to express it as positive, whereas negative values could prove useful in certain scientific applications, for instance when trying to analyze experimental methods by understanding whether measurements tend to overestimate or underestimate.

An often-made mistake involves miscalculating absolute error. Some may subtract estimated values from actual values without taking account of absolute values; this leads to incorrect conclusions and misinterpretations of measurements. Always ensure to calculate this difference so as to avoid misinterpretation of results.

Conclusion and Future Outlook

Percent error not only plays a vital role in scientific research but also pervades daily life applications. Being able to calculate percent error accurately assists in ensuring quality and reliability across various fields. As technology evolves, the future may hold advancements that allow for more sophisticated methods of measuring and analyzing error. Tools employing artificial intelligence and data analysis could enhance precision in calculations, minimizing errors in reporting. As science continues to evolve, improving our measurement techniques will remain essential to ensuring the integrity of data and research outcomes.

Reference:

https://www.lantmateriet.se/globalassets/om-lantmateriet/var-samverkan-med-andra/hmk/gum/riga_gum.pdf

https://www.indeed.com/career-advice/career-development/statistical-methods

https://www.employbridge.com/blog/career-path/what-are-5-different-quality-control-methods