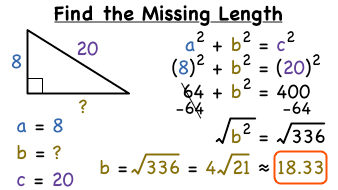What Is the Pythagorean Theorem?

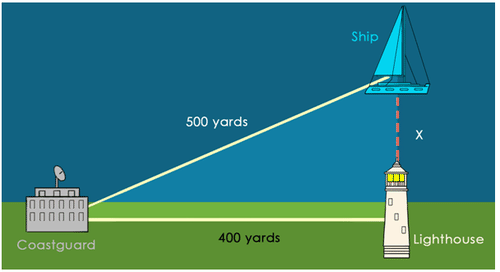
Geometry plays a central role in everyday life and presents many practical challenges requiring accurate measurements, like planning the layout of a new garden: when placing benches exactly at diagonal corners across rectangular lawns, one must determine distances precisely between opposing corners - this scenario naturally leads to one age-old geometric principle known as Pythagorean Theorem that determines relationships among sides in right triangles; its timeless beauty and mathematical precision lend themselves well to practical applications ranging from construction and design projects to navigation applications.

Overview of the Pythagorean Theorem

Statement and Definition of the Theorem  

Explanation of the Theorem’s Meaning  

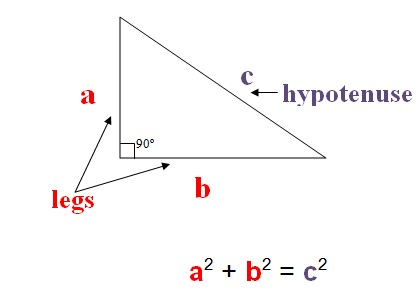
The Pythagorean Theorem, one of the cornerstones of Euclidean geometry, states that in any right-angled triangle, the sum of squares from both legs equals that of its hypotenuse. If we denote their lengths with letters$a$ and $b$ for legs A and B, and the length of the hypotenuse by $c$, then the equation

$a^2+b^2=c^2$

Under these conditions, this formula must hold. This simple yet profound equation exposes the intrinsic symmetry and logic governing these geometric relationships, offering deeper insight into space's physical makeup while serving as the cornerstone for numerous mathematical applications and real-world designs.

Conditions for the Theorem in Right-Angled Triangles  

The Pythagorean Theorem only applies when one angle in a triangle measures exactly 90 degrees; as such, it's vitally important that before applying this relationship $a^2+b^2=c^2$. You verify your triangle contains one right angle before proceeding further with any calculations using it. Failing this necessary condition means any calculations using this theorem would result in inaccurate calculations, so making sure there's at least one right angle present is key to using its effects reliably.

The Theorem’s Formula and Derivation  

Display of the Formula  

Pythagorean Theorem can be easily stated mathematically with these simple words:

$a^2+b^2=c^2$  

This concise formula quickly illuminates all three sides in any right-angled triangle and their interconnections.

Methods of Proof  

Mathematicians have created various techniques to demonstrate this timeless theorem; some of the more widely employed approaches include:

Algebraic Proof  

Imagine that we have a right triangle $△ABC$ with $\angle C=90^{\circ }$ and side lengths $AC=a$, $BC=b$ and hypotenuse length $AB=c$. One popular algebraic approach begins by creating squares on each side of the triangle, yielding areas of $a^2$, $b^2$, and $c^2$. Applying algebra's square of sum formula, we observe:

$(a+b{)}^2=a^2+2ab+b^2$  

By comparing the sums of areas on each leg with those on the hypotenuse and using careful rearrangement of terms, one can show this same point:

$a^2+b^2=c^2$  

Derivation involves carefully expanding expressions for areas of constructed squares on each of a triangle's sides, then subtracting any overlapped regions, if necessary, before isolating terms to reveal their intrinsic equality. Effectively, one transforms any geometric configuration into an equivalent algebraic equation by setting equal sums on certain areas. This approach employs basic algebraic identities such as the distributive law and expansion formula for squared binomials to provide a step-by-step progression, making math accessible even to novice students by showing clearly how geometric properties lead naturally to algebraic outcomes. This technique greatly assists those new to mathematics as it clearly displays how geometric figures have inherent properties that lead to algebraic outcomes.

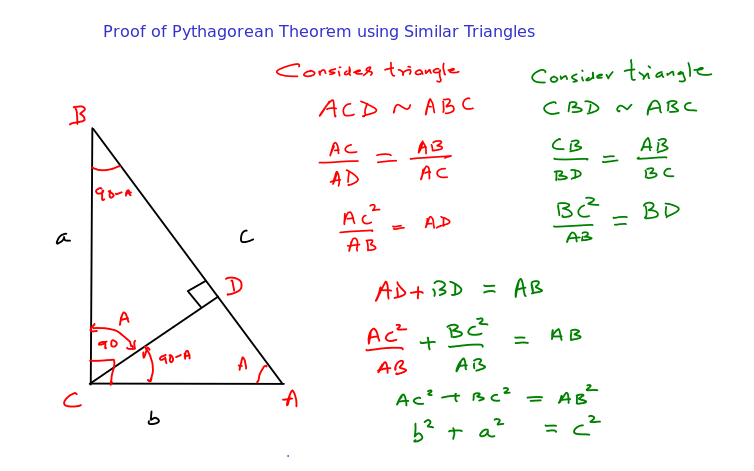
Proof by Similar Triangles  

Take $△ABC$ as an example, with $\angle C=90^{\circ }$and altitude from $C$ meeting at point $D$ of its hypotenuse $AB$ at $D$, creating two smaller triangles similar to $△ABC$such as(\triangle ADC\) and $△CBD$ that share properties similar to themselves as well. Assume these relationships hold between similar triangles:

$\frac{AC}{AB}=\frac{CD}{BC}\text{and}\frac{BC}{AB}=\frac{CD}{AC}$  

Moreover, from the similarity, we obtain the relations:  

$A{C}^2=AB\cdot AD\text{and}B{C}^2=AB\cdot DB$  

Since $AD+DB=AB$, adding the two equations yields:  

$A{C}^2+B{C}^2=AB\cdot (AD+DB)=AB\cdot AB=A{B}^2$  

That is,  

$a^2+b^2=c^2$  

By exploiting the ratios inherent to similar triangles and partitioning the hypotenuse, this approach offers an intuitive geometric visualization of Pythagorean theorem. Not only does it beautifully connect algebraic expressions with geometric figures; but also illustrates how proportional relationships within triangles naturally give rise to Pythagorean relationship.

Historical Development

Discovery of the Theorem in Ancient Civilizations  

Early Applications in Ancient Egypt and Babylon  

As early as several millennia ago, artisans in ancient Egypt and Babylon used principles similar to those behind the Pythagorean Theorem when designing structures or measuring land. Egyptian craftspeople utilized rope knots with right angle triangles tied on them when building pyramids or temples to ensure stability while clay tablets from Babylon reveal numerous numerical combinations suggesting they had developed expertise at verifying relationships among shapes through numerical means; providing practical evidence of what later evolved into Pythagorean Theorem.

Contributions from Ancient Indian and Chinese Mathematics  

Ancient Indian mathematical texts contain descriptions reminiscent of the Pythagorean Theorem, and Chinese literature like "Zhou Bi Suan Jing" records relationships among right triangle sides that reflect its embryonic development into "Gougu," or Pythagorean concepts. Mathematicians in both civilizations not only verified the correctness of this theorem but also created numerous tools related to practical measurements and astronomical calculations to demonstrate an Eastern-Western interdependency within ancient cultures.

The Pythagorean School and the Naming of the Theorem  

The Pythagorean School formalized and formalized proof for this theorem, making it a cornerstone in Greek mathematical history. Subsequently, to honor Pythagoras and his followers, this theorem came to be known as the "Pythagorean Theorem." Its impact spanned not just math development but philosophy and natural sciences.

The Development of the Theorem in Medieval and Modern Mathematics  

Medieval Islamic scholars were instrumental in refining and modernizing Greek mathematics. Through improved proof techniques based on existing theories, Islamic scholars strengthened the Pythagorean Theorem while strengthening methods of proof. With Renaissance mathematics and later Euclid's studies establishing it as part of analytic geometry and trigonometry studies as part of analytic geometry and trigonometry theories, furthering advancements in both pure mathematics as well as applied sciences such as physics and engineering.

Applications and Practices of the Pythagorean Theorem

Real-World Application Scenarios  

Cases in Engineering, Architecture, and Navigation  

Pythagorean Theorem remains an indispensable tool in many fields, such as engineering construction, architectural design, navigational positioning and more. For instance, architects use right triangle properties to calculate distances precisely between various structural components to maintain stability and aesthetic appeal of buildings or bridges or high-rise structures such as overpasses, often employing its formula when planning these overpasses.

$a^2+b^2=c^2$  

Navigation systems—particularly aviation and maritime ones—rely on data derived from right triangles to calculate straight-line distances between points for precise positioning. Engineers also employ this principle in land surveying and road planning projects to ensure every detail satisfies stringent measurement standards.

Example Problem Analysis  

Hypotenuse Calculation Example  

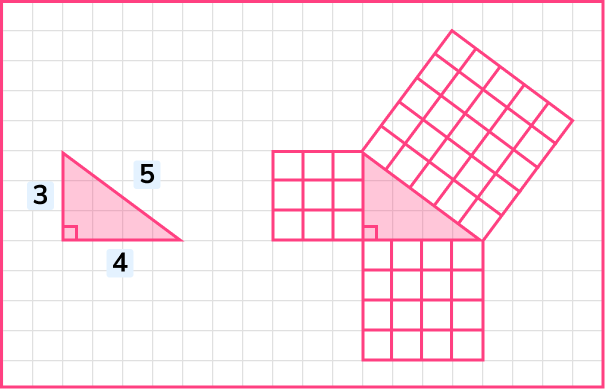
Consider a right triangle with legs measuring 3 meters and 4 meters; to calculate its hypotenuse length according to Pythagorean Theorem, $3^2+4^2=c^2$, use these measurements.

Calculations yield $9+16=25=c^2$, so the hypotenuse length $c=\sqrt{25}=5$ . This simple example shows how this theorem can quickly determine required lengths in architectural components or bridge designs.

Leg Calculation Example  

If one leg of a right triangle is 5 meters and the hypotenuse is 13 meters, to find the length of the other leg, let the unknown leg be $b$. Then, by the theorem  

$5^2+b^2=13^2$  

We get: $25+b^2=169$. Rearranging yields $b^2=144$, hence $b=\sqrt{144}=12$ meters.  

This problem not only tests one's knowledge and application of formulae but also trains one's sensitivity during mathematical derivations.

Through these examples and analyses, it becomes evident that the Pythagorean Theorem not only has rigorous logic and geometric appeal in theory but is also an efficient computational tool in practice—from land surveying to construction to modern navigation technologies—where its existence remains indispensable.

How to Correctly Use the Pythagorean Theorem

Steps and Precautions for Use  

Before applying the Pythagorean Theorem in practice, it must first be confirmed that the triangle under consideration is indeed right-angled. To accomplish this step effectively: first, use measuring instruments to ascertain the lengths of triangle sides and confirm whether there exists an angle of 90deg; second, based on properties associated with right triangles label two of its sides as "a and b," with its hypotenuse identified by "c," then apply the formula  

$a^2+b^2=c^2$  

for calculation and verification. Thirdly, carefully inspect each step in the calculation and verification processes in order to guarantee error-free algebraic operations; when measuring with the theorem, it's also vitally important that units and precision data remain consistent for accurate measurements that do not lead to further calculation errors; additionally selecting appropriate calculation and verification techniques in both engineering and mathematical tests can produce more reliable results; these steps not only assist beginners systematically understanding its use but provide scientific proof in solving real-world issues.

Common Misconceptions and Their Corrections  

Before embarking upon any process, it is crucial that the operation steps be followed properly, as well as understanding any common misconceptions that might occur, including wrongly applying the theorem to triangles that do not form right angles or confusing legs and hypotenuse in formulae (when really only hypotenuse exists). It is crucial that both procedures be carried out precisely because mistakes could lead to false results that alter how one interprets reality. In reality, the formula  

$a^2+b^2=c^2$  

only holds when it is proven that the triangle has right angles. Therefore, it is wise to first verify any angle measurements or use additional tools for measurement to validate each step in your calculations. With the practice of following correct procedures and an awareness of common pitfalls in problem-solving using the Pythagorean Theorem, you will become adept and precise at using it to solve practical issues more efficiently and precisely, further increasing the efficiency and precision of mathematical problem-solving techniques.

Applications of the Pythagorean Theorem in Non-Traditional Fields  

The Pythagorean theorem is well known as part of classical geometry; however, its influence extends far beyond this realm. Digital art and computer graphics, for instance, rely on this theorem as an aid to accurately calculate distances between pixels, ensuring smooth transitions and realistic perspectives. Data scientists also utilize its principles when measuring distances across multidimensional spaces, improving the performance of clustering and classification algorithms. Roboticists rely on mathematical techniques such as movement planning and sensor fusion to design precise navigational systems for robotics. Music theory also benefits from abstract interpretations of these theorems that provide methods of examining sound frequencies and harmonics. Architects and engineers apply these concepts when designing modern structures, striking a balance between aesthetic creativity and structural soundness. It serves as a reminder that scientific disciplines and creative endeavors are inextricably intertwined. His lasting legacy shows how fundamental mathematical principles can stimulate innovation in fields beyond mathematics itself, opening doors for breakthrough technologies and methods. Furthermore, this exploration shows how ancient mathematical ideas still hold relevance today while continuously adapting to meet modern challenges by connecting theory with creativity and technology and inspiring further study.

Through this article, it becomes apparent that the Pythagorean Theorem is more than simply an abstract mathematical concept - it represents ancient and modern wisdom coming together through mathematics. From early applications in ancient civilizations to innovative explorations with AR/VR technology and everything in between demonstrates mathematics' charm. With lively language, this article analyzes its concept, historical development, practical applications and common misconceptions before encouraging students to discover it for themselves in everyday life situations - with this comprehensive summary, hoping to encourage more people to view life through mathematical lenses!

reference：

https://en.wikipedia.org/wiki/Pythagorean_theorem

https://en.wikipedia.org/wiki/Right_triangle

https://en.wikipedia.org/wiki/Similarity_(geometry)