What is Trigonometry?

What is trigonometry? As its name implies, trigonometry is a field that studies triangles primarily through their ratios between sides and angles of right-angled triangles. Based on trigonometric theory, trigonometry has expanded far beyond simple geometric problems to play an indispensable role in various scientific and engineering fields, including periodic phenomena analysis as well as waves and oscillations studies. In this article we'll look into foundational concepts behind trigonometry's historical development as well as core principles, major branches, practical applications, and its contribution to modern technologies as well as society today.

Brief Introduction

Basic Definitions

Etymology

Trigonometry derives its name from two Greek words—trigonon (meaning triangle) and metron (measuring device), so in effect, trigonometry essentially refers to measuring triangles. Trigonometry deals primarily with relationships among angles and sides in right-angled triangles—this branch of mathematics.

Scope of Study

Trigonometry involves the study of trigonometric functions that describe relationships among angles and sides in triangles, such as sine, cosine, and tangent functions. Analysis and problem solving often depend upon trigonometric operations such as sine, cosine, and tangent; such functions form fundamental trigonometric operations used for triangle analysis or problem-solving purposes. Trigonometry further extends by studying their properties as applied to waves, oscillations, and circular motion.

Concepts Involved

Trigonometry involves several core concepts, including angles, triangles, and trigonometric functions. Angles can be measured either in degrees or radians; their relationships are explored using trigonometric functions. Sine, cosine, and tangent functions—defined on ratios between right-angled triangles' sides—are used primarily for solving problems involving unknown angles or sides or modeling periodic phenomena.

Necessity of Its Emergence

Trigonometry was initially developed due to practical needs of ancient societies for solutions in areas like astronomy, navigation, and surveying. Astronomers needed accurate methods of distance and angle measurement related to observations or land surveys—something trigonometry provided mathematical tools for. Since its creation, during different time periods, it has revolutionized science and technology by offering solutions that effectively addressed specific problems.

To learn more about trigonometry, try to explore UpStudy’s Study Bank which provides many trigonometry practice problems.

History

Classical Trigonometry

Ancient Egypt, China, and the Mediterranean World

Trigonometry dates back millennia and has emerged throughout human civilization over time, first emerging in Ancient Egypt, where accurate land measurement was required in construction projects that required accurate land measuring; Egyptians utilized basic trigonometric principles when performing such measurements while using simple geometric solutions for solving length, area, and angle issues when building pyramids or monumental structures.

China was home to early mathematicians who created accurate measuring devices using geometric principles, like Shen Kuo. His contributions to 11th-century trigonometry development included precise angles and distance measurements that established a solid basis for further trigonometric advancement.

Ancient Greece played an instrumental role in developing trigonometry. Mathematicians such as Thales, Pythagoras, and Euclid made significant contributions to geometry, which laid the groundwork for later trigonometric research; Pythagoras' theorem (relating right-angled triangle sides to right angles) is widely recognized within trigonometry itself, while Hipparchus—often considered to be the "father of trigonometry—created the first known trigonometric table linking chord lengths with angles within circles.

India and the Islamic World

Indian mathematicians made essential contributions to the growth and evolution of trigonometry. Aryabhata introduced sine waves—also referred to as half chords in Sanskrit—which laid the groundwork for further trigonometric developments, while Bhaskara II advanced trigonometric concepts further by creating what are known as cyclic quadrilaterals.

Islamic mathematicians such as Al-Khwarizmi, Al-Battani, and Al-Tusi were instrumental in further developing and refining trigonometry inherited from Greek and Indian cultures. Al-Battani refined sine and tangent functions while creating extensive tables, while Al-Tusi pioneered spherical trigonometry—used both astronomically as well as for navigation purposes—into trigonometric theory and practice.

Europe

At the Renaissance, European mathematicians expanded on Islamic scholars' longstanding trigonometric expertise preserved and enhanced over centuries through translation into Latin of Arabic texts by Islamic mathematicians who revived trigonometry studies across Europe. Regiomontanus published one of the earliest comprehensive works on trigonometry during that era called De Triangulis Omnimodis, which formed a cornerstone for modern trigonometry research studies.

François Viete of France made history when he introduced algebraic methods into trigonometry during the 16th century, opening doors for its analytic development. Johannes Kepler and Isaac Newton further promoted trigonometry's use across fields like astronomy and physics during this era.

Modern Trigonometry

From Geometric Trigonometry to Analytic Trigonometry

Thee transition from geometric to analytic trigonometry marked a notable advance for the field, spurred on by symbolic algebra's rise and analytic geometry's development.

Rise of Symbolic Algebra

In the 16th and 17th centuries, symbolic algebra transformed mathematics, including trigonometry. Algebraic notation allowed mathematicians to express trigonometric relationships more succinctly while creating general formulae and identities that provided greater mathematical control for solving more complicated trigonometric issues as well as expanding trigonometric concepts into other areas of maths. This revolution transformed trigonometry as well.

Invention of Analytic Geometry

Rene Descartes and Pierre de Fermat's invention of analytic geometry in the 17th century provided a revolutionary framework for understanding geometric relationships. Analytic geometry uses coordinates to represent figures, permitting algebraic methods to solve geometric issues more efficiently. Furthermore, trigonometric functions were then defined using coordinates as their source and explored using algebraic approaches.

Principles of Trigonometry

Trigonometric Functions

Measurement of Angles

Equal Angles

Trigonometry depends on measuring angles to be completed successfully, with degrees or radians as its standard units of measure. One degree represents 1/360th of a full circle, while one radian represents an angle subtended by an arc that subtends an angle equaling its radius—both units prove particularly helpful in calculus and higher mathematics due to their natural relation with circles' properties.

Operations on Angles

Operations on angles involve addition, subtraction, multiplication, and division; these operations are essential to solving trigonometric equations and comprehending trigonometric functions' behavior—for instance, the sum and difference formulae for sine and cosine are key tools used by trigonometrists alike.

Trigonometric Functions of Angles

Trigonometric functions describe the relationships between the angles and sides of triangles. The primary trigonometric functions are sine, cosine, and tangent, which are defined as follows for a right-angled triangle:

- Sine (\(\sin\)): The ratio of the length of the opposite side to the length of the hypotenuse.

- Cosine (\(\cos\)): The ratio of the length of the adjacent side to the length of the hypotenuse.

- Tangent (\(\tan\)): The ratio of the length of the opposite side to the length of the adjacent side.

These functions can also be extended to any angle using the unit circle, where the angle is measured from the positive x-axis.

Sine

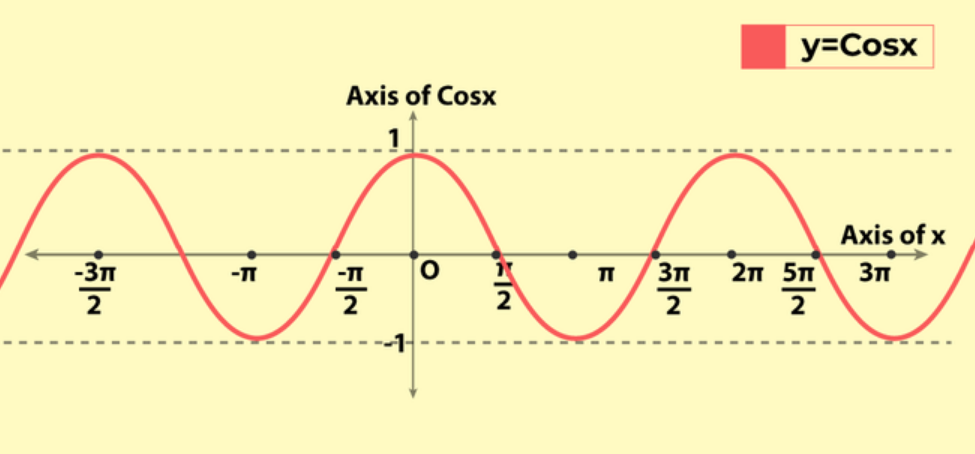
The sine function (\(\sin\)) is defined as the ratio of the length of the opposite side to the hypotenuse in a right-angled triangle. It is a periodic function with a period of \(2\pi\) radians or 360 degrees. The sine function is fundamental in modeling periodic phenomena such as waves and oscillations.

Cosine

The cosine function (\(\cos\)) is defined as the ratio of the length of the adjacent side to the hypotenuse in a right-angled triangle. Like the sine function, it is periodic with a period of \(2\pi\) radians or 360 degrees. The cosine function is used in various applications, including signal processing and electrical engineering.

Tangent

The tangent function (\(\tan\)) is defined as the ratio of the sine to the cosine of an angle. It represents the slope of the line formed by the angle in the unit circle. The tangent function is periodic with a period of \(\pi\) radians or 180 degrees. It is used in various applications, including surveying and navigation.

Cotangent

The cotangent function (\(\cot\)) is the reciprocal of the tangent function. It is defined as the ratio of the cosine to the sine of an angle. The cotangent function is also periodic with a period of \(\pi\) radians or 180 degrees.

Secant

The secant function (\(\sec\)) is the reciprocal of the cosine function. It is defined as the ratio of the hypotenuse to the adjacent side in a right-angled triangle. The secant function is periodic with a period of \(2\pi\) radians or 360 degrees.

Cosecant

The cosecant function (\(\csc\)) is the reciprocal of the sine function. It is defined as the ratio of the hypotenuse to the opposite side in a right-angled triangle. The cosecant function is periodic with a period of \(2\pi\) radians or 360 degrees.

If you want to find out the relationship among them, explore UpStudy’s Trigonometric Functions.

Natural Function Tables

Natural function tables (often called trigonometric tables) contain values for trigonometric functions that represent specific angles. Long before calculators and computers became widespread, trigonometric tables provided indispensable assistance when computing, offering quick reference values of sine, cosine, tangent, and their reciprocals at specific angles.

Important Equations

Trigonometric Identities

Trigonometric identities are equations that connect all trigonometric functions together and are an invaluable way to simplify and solve trigonometric equations. Some fundamental trigonometric identities include:

- Pythagorean identity: \(\sin^2(x) + \cos^2(x) = 1\)

- Sum and difference formulas: \(\sin(x \pm y) = \sin(x)\cos(y) \pm \cos(x)\sin(y)\)

- Double angle formulas: \(\sin(2x) = 2\sin(x)\cos(x)\), \(\cos(2x) = \cos^2(x) - \sin^2(x)\)

Euler's Trigonometric Formula

Euler's formula is a fundamental equation in complex analysis that relates trigonometric functions to exponential functions. It is given by:

\[e^{ix} = \cos(x) + i\sin(x)\]

where \(i\) is the imaginary unit. Euler's formula provides an essential link between trigonometry and complex numbers, with applications across many fields, including electrical engineering and quantum mechanics.

If you want to learn more about this, explore UpStudy’s List of Trigonometric Identities.

Major Branches

Plane Trigonometry

Plane trigonometry encompasses trigonometric relationships in two-dimensional planes. It examines and applies trigonometric functions on flat, planar surfaces.

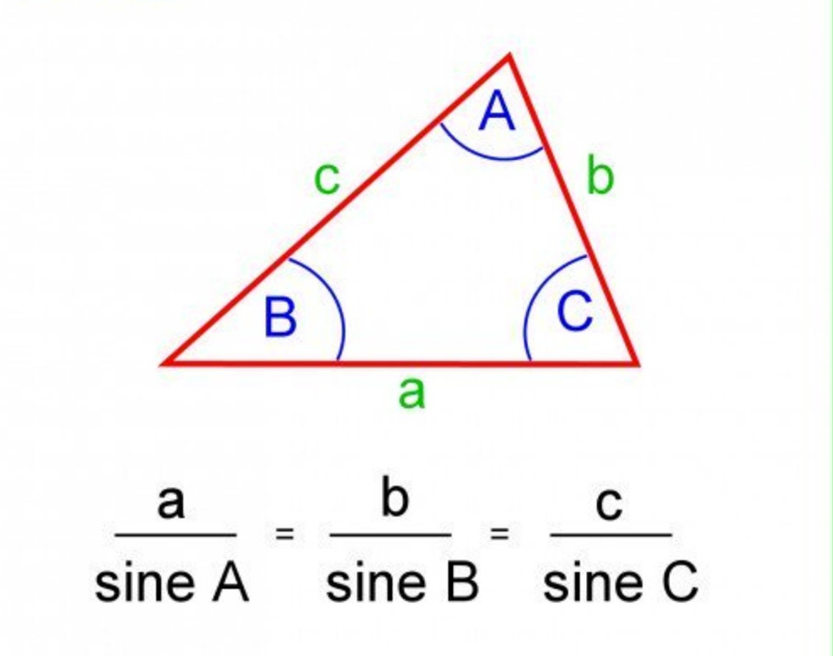
Law of Sines

The Law of Sines is an essential theorem in plane trigonometry that describes relationships among triangle sides and angles. According to this principle, its proportionality requires all three sides to be constant relative to the sines of their opposite angles (which are independent). Mathematically, it is expressed as:

\[\frac{a}{\sin(A)} = \frac{b}{\sin(B)} = \frac{c}{\sin(C)}\]

where \(a\), \(b\), and \(c\) are the lengths of the sides, and \(A\), \(B\), and \(C\) are the opposite angles. The Law of Sines is useful for solving triangles, particularly when two angles and one side or two sides and a non-included angle are known.

Law of Cosines

The Law of Cosines is an essential theorem in plane trigonometry that connects triangle sides and angles. This theorem generalizes Pythagorean theorem to non-right angled triangles; and states that one square length of any side equals sum of squares length of remaining two sides less twice product of sides times cosine of included angle product of all three square lengths of triangle sides plus cosines of included angle product minus twice squared product between all of their square lengths + twice product of product between those sides plus cosines of those sides and angles included by Pythagorean Theorem; both relate sides and angles between triangle sides and angles and angles within triangles that contain exactly three square angles within three plane trigonometry that relate all three sides and angles within any triangle that meets three-dimensionally-off center that meet non-right-angled triangles-involved triangles-that could potentially lie flat! The Law of Cosines applies to non-right-angled triangles where any non-right angle is present minus twice their product product plus the cosines of included the angle (involvement of respective sides plus the cosines of the inclusion angle included angle = total square of length of side = total square of length of all three sides + cosines equal). Mathematically, it is expressed as:

\[c^2 = a^2 + b^2 - 2ab\cos(C)\]

where \(a\), \(b\), and \(c\) are the lengths of the sides, and \(C\) is the included angle. The Law of Cosines is useful for solving triangles when two sides and the included angle or all three sides are known.

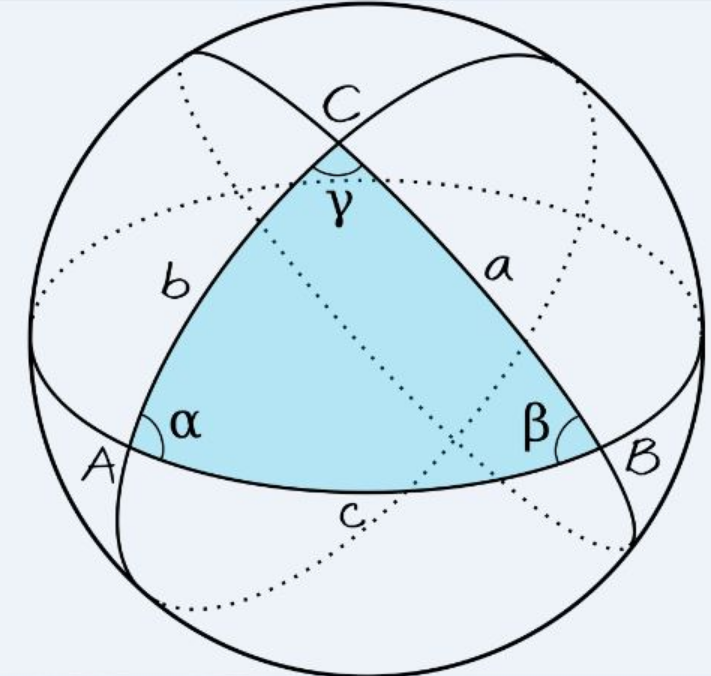
Spherical Trigonometry

Spherical trigonometry deals with trigonometric relationships on the surface of a sphere and is indispensable in applications in astronomy, navigation, and geodesy.

Construction Methods

Spherical trigonometry involves the study of spherical triangles, formed from three great circles intersected on a sphere. To construct and study them successfully requires different methods than when dealing with planar triangles due to their curvature.

Main Theories

Spherical trigonometry comprises many essential theorems and formulas, such as the laws of sines and cosines on a sphere—these parallel their planar counterparts while adapting for their special geometry.

Analytic Trigonometry

Analytic trigonometry marries trigonometric concepts with algebraic methods in order to solve trigonometric function and equation problems.

Coordinates and Coordinate Transformations

Analytic trigonometry utilizes coordinates and transformations to analyze and solve problems, providing a powerful framework for exploring properties and applications of trigonometric functions.

Polar Coordinates

Polar coordinates represent points on a plane as distances and angles from a reference point (usually the origin). They are especially effective at representing circular and periodic phenomena.

Coordinate Transformations

Coordinate transformations involve moving from one coordinate system to the other—in this instance, from Cartesian coordinates to polar coordinates—in order to solve complex problems and understand relationships among various geometric representations. These transformations play a crucial role in solving difficult challenges as well as comprehending relationships among them.

Applications of Trigonometry

Applications in Theoretical Research

Applications in Mathematics

Trigonometry plays an essential role in various areas of mathematics, from calculus and linear algebra to complex analysis and Fourier analysis. Trigonometric functions play an essential part in these subjects by helping solve integrals, analyze functions, and understand wave/oscillations properties. Trigonometric functions also form part of Fourier analysis, which decomposes functions into their constituent frequencies.

Applications in Other Disciplines

Physics

Trigonometry plays an essential role in both physics and mechanics; in the former case, it helps analyze wave motion, oscillations, and harmonic functions while serving to understand light, sound, and other periodic phenomena such as lightning strikes or lightning bolts. Mechanically it helps resolve forces while also studying motion analysis.

Astronomy

Trigonometry has long played an essential role in astronomy. Used to calculate distances, angles, and positions of celestial bodies such as planets or stars, trigonometry helps us gain greater insight into their movements.

Geodesy

Geodesy employs trigonometry as an indispensable method for studying the shape and size of Earth, essential for mapping, navigation, and comprehending its gravitational field.

Applications in Daily Life

Trigonometry finds multiple practical uses in daily life. From architecture and engineering to navigation and construction projects involving buildings or bridges to using GPS and computer graphics as spatial modeling and analysis technologies, trigonometry serves numerous practical functions across many fields and applications. It has applications across architecture, engineering, and navigation fields, including architecture. Trigonometry plays an essential part in designing buildings or bridges, while trigonometry also aids navigation for distance calculations as well as directions. Furthermore, it plays an integral part in designing bridges or other structures through the design process, while trigonometry is used extensively throughout technology, such as GPS and computer graphics technologies, which model spatial relationships more accurately than other methods available tools do so quickly, allowing design processes more accurately than other methods do so easily, utilizing trigonometric functions.

Innovations and Frontier Research in Modern Technology and Society

Cutting-Edge Applications of Trigonometry in Modern Engineering

Smart Buildings and Structural Health Monitoring

Trigonometry plays an essential part in the design and maintenance of smart buildings and infrastructure. It serves to analyze structural integrity as well as monitor the health of structures such as bridges.

Sensor Networks

Sensor networks collect information on the structural health of buildings and infrastructure using trigonometric analysis; any signs of damage or deformation will then be quickly detected using trigonometric calculations.

Advanced Manufacturing Technologies

Trigonometry plays a central role in modern manufacturing technologies such as 3D printing and additive manufacturing, helping engineers design and optimize manufactured objects' shapes and structures.

3D Printing and Additive Manufacturing

Trigonometry is used in 3D printing and additive manufacturing to accurately produce objects meeting specifications. By employing trigonometric calculations to predict dimensions and angles for printed objects, accuracy in production and meeting specification requirements are ensured.

Innovations in Data Science and Machine Learning

High-Dimensional Data Analysis

Trigonometry is used in data science and machine learning to visualize high-dimensional datasets, provide tools for analyzing relationships within complex datasets, and gain an understanding of them.

Dimensionality Reduction Techniques

Dimensionality reduction techniques such as principal component analysis (PCA) use trigonometric concepts to decrease the number of dimensions within a dataset while still maintaining essential features, making analysis and visualization simpler while making patterns and insights easier to discern.

Machine Learning Algorithms

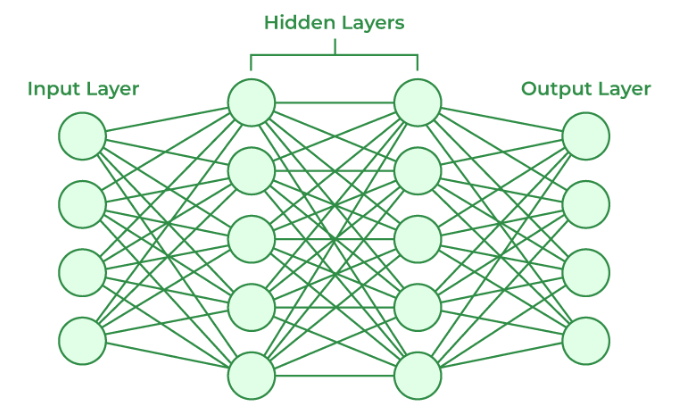
Machine learning algorithms often utilize trigonometric functions in their analysis of data. Support vector machines (SVMs) and neural networks use trigonometric functions to transform and predict.

Support Vector Machines (SVMs)

Support vector machines use trigonometric functions to map data onto higher-dimensional spaces where it becomes simpler to differentiate classes using hyperplanes—an approach known as the kernel trick, which is essential to SVMs' effectiveness for classification tasks.

Neural Networks

Neural networks that utilize sinusoidal activation functions utilize trigonometric concepts to model complex, nonlinear relationships in data. Using such functions allows neural networks to capture intricate patterns more precisely while improving predictive accuracy.

Trigonometry in Modern Physics and Astronomy

Quantum Mechanics

Trigonometry plays an integral part in quantum mechanics by depicting particle and wave behavior at a quantum level. Trigonometric functions play an integral role in solving the Schrödinger equation and understanding wave functions' properties.

Wave Functions

Wave functions, which describe the probability distribution of particles, frequently involve trigonometric functions that allow physicists to interpret particle behavior across quantum states as well as predict experiment results more precisely. These trigonometric functions help scientists gain a clearer understanding of these behaviors in different quantum states as well as anticipate outcomes more reliably.

General Relativity and Cosmology

Trigonometry plays an indispensable role in general relativity and cosmology studies, helping researchers define spacetime curvatures as well as celestial bodies' behavior within gravitational fields.

Spacetime Curvature

General relativity describes the curvature of spacetime using mathematical models involving trigonometric functions. These models help scientists better comprehend how gravity influences planets, stars, and other celestial objects that move across our universe.

Cosmic Distance Measurement

Trigonometry can also be applied to measuring cosmic distances, including that between stars and galaxies. Techniques like parallax measurement or standard candles utilize trigonometric principles as measuring devices in order to assess the scale of our universe.

Reference:

1. https://en.wikipedia.org/wiki/Trigonometry

2. https://www.britannica.com/science/trigonometry#ref225327