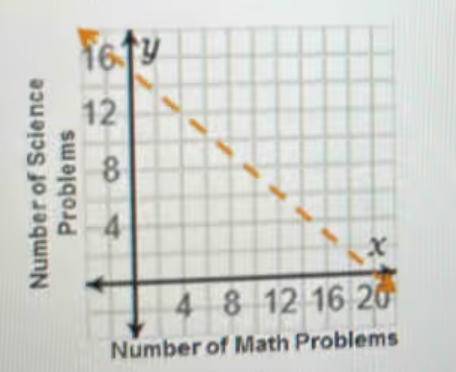
Alexia spent 3 minutes working on each of her math problems and 4 minutes on each of her science problems. Her homework took her more than 60minutes to complete. The boundary line for the inequality 3x+4y>60 is shown.Which statement could be true in this situation?Alexia completed 8 math problems and 9 science problems.Alexia completed 4 math problems and 6 science problems.Alexia completed 20 math problems and 10 science problems.Alexia completed no math problems and 15 science problems.

To determine which statement could be true, we need to check which combination of math and science problems satisfies the inequality \(3x + 4y > 60\), where \(x\) is the number of math problems and \(y\) is the number of science problems.

1. 8 math problems and 9 science problems:
   \[3( 8) + 4( 9) = 24 + 36 = 60 \quad \text { ( This is exactly 60, so it does not satisfy \(> 60\)) } \]
2. 4 math problems and 6 science problems:
   \[3( 4) + 4( 6) = 12 + 24 = 36 \quad \text { ( This is less than 60, so it does not satisfy \(> 60\)) } \]
3. 20 math problems and 10 science problems:
   \[3( 20) + 4( 10) = 60 + 40 = 100 \quad \text { ( This is greater than 60, so it satisfies \(> 60\)) } \]
4. No math problems and 15 science problems:
   \[3( 0) + 4( 15) = 0 + 60 = 60 \quad \text { ( This is exactly 60, so it does not satisfy \(> 60\)) } \]

Supplemental Knowledge

Understanding linear inequalities is crucial for solving problems involving constraints and optimization. Here are some key concepts:

Key Concepts:

1. Linear Inequality:
   • An inequality that involves a linear function.
   • Example: \(3x + 4y > 60\).
2. Boundary Line:
   • Represents the equation \(3x + 4y = 60\).
   • The inequality \(3x + 4y > 60\) means the solution lies above this line.
3. Graphing Inequalities:
   • Plot the boundary line first.
   • Use a test point to determine which side of the line satisfies the inequality.
4. Feasible Region:
   • The area where all conditions of the inequality are met.
   • For \(3x + 4y > 60\), it’s the region above the boundary line.

Everyday Examples

Imagine creating a study schedule with limits on how much time can be dedicated to different subjects. If homework requires spending over an hour per subject, using an inequality to represent this constraint and graph it can help visualize your options and better organize study.
Plotting these on a graph enables you to see combinations that meet your study goals without exceeding time restrictions and avoid time wasting.

At UpStudy, we believe mastering algebraic concepts like linear inequalities can open doors to better problem-solving skills in real life. Our Algebra Inequalities Calculator is designed to help you understand and solve these problems efficiently. Dive into our resources today and make complex math simple with UpStudy!
For further assistance with algebraic inequalities, explore UpStudy’s Algebra Inequalities Calculator!