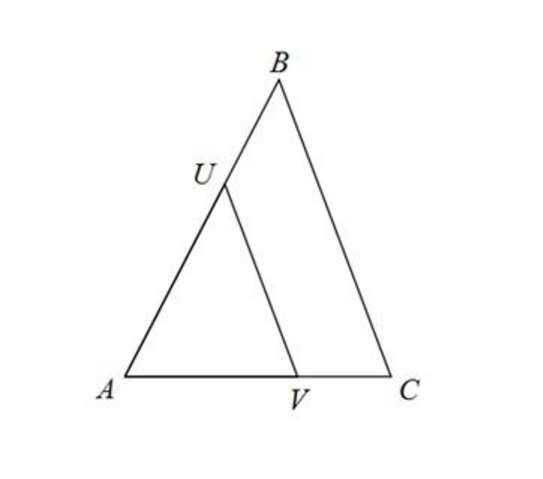
Given that the two triangles are similar, solve for x if AU = 20x + 108, UB = 273, BC = 703, UV = 444, AV = 372 and AC = 589.

Step 1: 
Given that the two triangles \(\triangle AUV\) and \(\triangle ABC\) are similar, their corresponding sides are proportional. 
 

Step 2:

The proportion can be set up as follows: 
\[\frac { AU} { AB} = \frac { UV} { BC} = \frac { AV} { AC} \]

Step 3: 
Using the given lengths: 
\[\frac { AU} { AU + UB} = \frac { UV} { BC} = \frac { AV} { AC} \]

Step 4: 
Substitute the given values: 
\[\frac { 20x + 108} { 20x + 108 + 273} = \frac { 444} { 703} = \frac { 372} { 589} \]

Step 5: 
Simplify the equation for \(x\): 
\[\frac { 20x + 108} { 20x + 381} = \frac { 444} { 703} \]

Step 6: 
Cross-multiply to solve for \(x\): 
\[( 20x + 108) \times 703 = 444 \times ( 20x + 381) \]\[14060x + 75924 = 8880x + 169164\]

Step 7: 
Rearrange to isolate \(x\): 
\[14060x - 8880x = 169164 - 75924\]
\[5180x = 93240\]
\[x = \frac { 93240} { 5180} \]
\[x = 18\]
 

Supplemental Knowledge:

When two triangles are similar, their corresponding sides are proportional. This means that the ratios of the lengths of corresponding sides are equal.

Steps to Solve: 
1. Identify the corresponding sides of the similar triangles. 
2. Set up a proportion using the given side lengths. 
3. Solve for the unknown variable.

Real-Life Connections:

Solving problems involving triangles and proportions is crucial in real-life scenarios. Understanding this technique will assist with problem-solving for future endeavors.
Imagine yourself as an architect designing a scaled-down model of a building. Knowing how to apply proportions will allow for accuracy when replicating its full scaled counterpart in miniature form.

To master essential skills like solving problems with similar triangles or explore other important mathematical concepts, check out UpStudy’s live tutor question bank! Our AI-powered problem-solving services provide detailed explanations and insights across various subjects—including a Geometry calculator.

Whether you're preparing for exams or simply passionate about improving your practical skills, UpStudy offers comprehensive resources tailored to your educational needs. Discover how UpStudy can support your academic journey today!