\log_3 2x=9
error msg
- Differential
- Integral
- Trigonometry
- Letters
- Algebra
- Calculus
- Trigonometry
- Matrix
Question
\log_{3}{\left(2x\right)}=9
Solve the equation
x=\frac{19683}{2}
Alternative Form
x=9841.5
Evaluate
\log_{3}{\left(2x\right)}=9
Find the domain
More Steps
Evaluate
2x>0
Rewrite the expression
x>0
\log_{3}{\left(2x\right)}=9,x>0
\text{Convert the logarithm into exponential form using the fact that }\log_{a}{x}=b\text{ is equal to }x=a^{b}
2x=3^{9}
Evaluate the power
2x=19683
Divide both sides
\frac{2x}{2}=\frac{19683}{2}
Divide the numbers
x=\frac{19683}{2}
Check if the solution is in the defined range
x=\frac{19683}{2},x>0
Solution
x=\frac{19683}{2}
Alternative Form
x=9841.5
Show Solutions
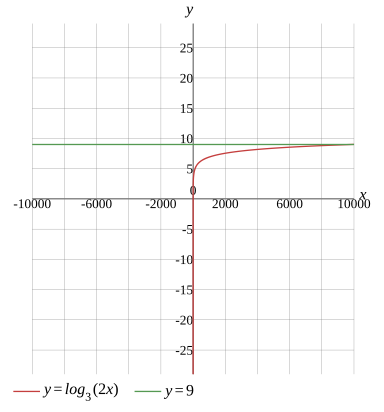
Graph