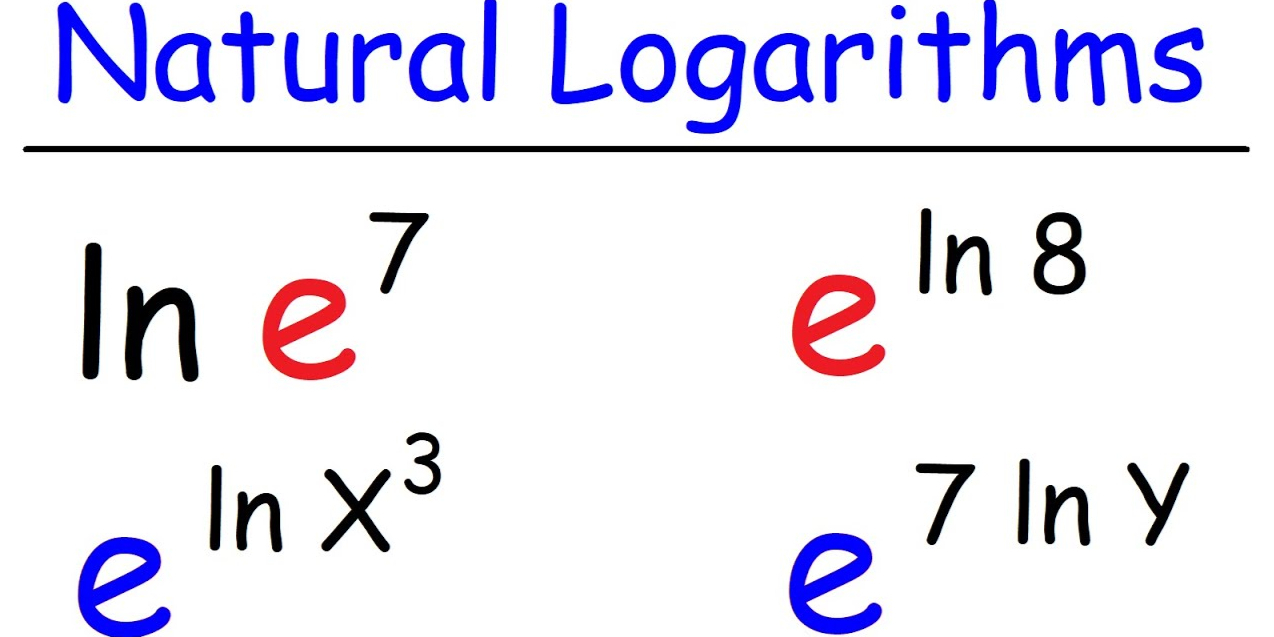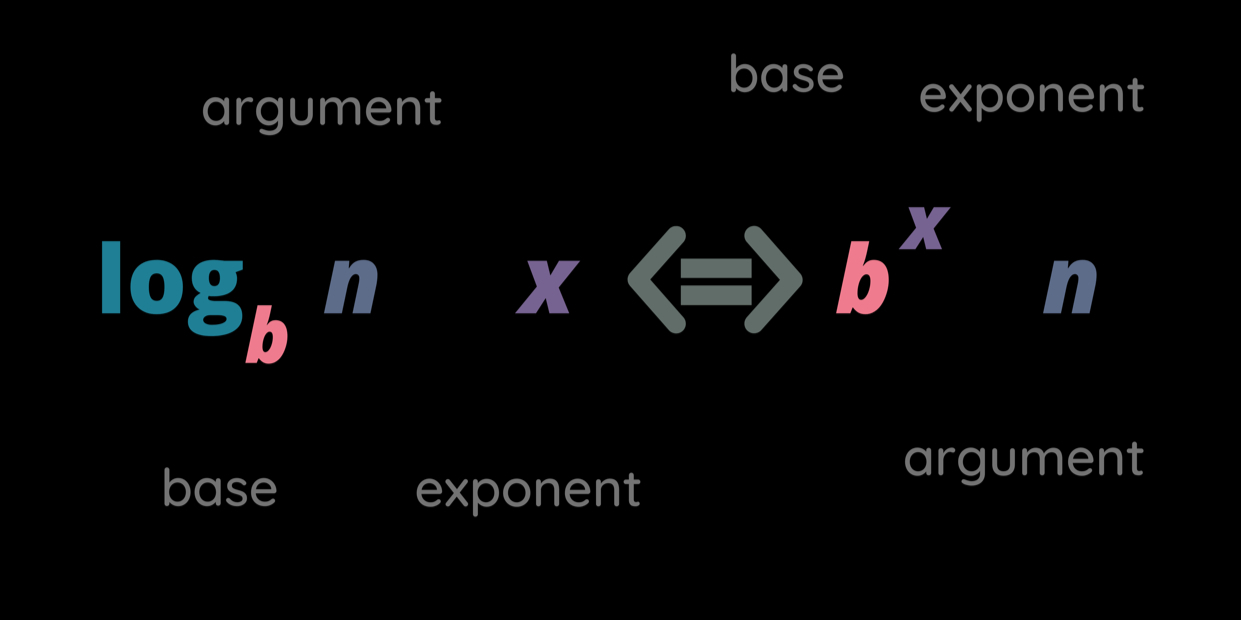What Is Algebra?

As one of the oldest branches of mathematics, algebra pervades our everyday lives in many forms. When purchasing a house, most find it challenging to pay all at once; how can they obtain loans and choose an installment plan with optimal cost-efficiency? Remodeling plans provide even greater financial value-add when choosing which plan offers maximum return for money spent—both are situations in which algebra comes in handy, not as just some mathematical symbols we rarely encounter but instead as a powerful tool we rely upon every moment!

Definition

Basic Definition

In its narrow sense, algebra refers to solving equations and finding unknown values through operations and symbols. This involves manipulating variables and constants to solve for unknowns in equations such as \(2x + 3 = 7\), where the goal is to determine the value of \(x\). In its broad sense, algebra encompasses a more extensive range of mathematical structures, relationships, and operations. It includes the study of polynomial functions like \(f(x) = x^2 + 3x + 2\), which involves understanding how variables interact within equations.

Etymology

Algebra derives its name from an Arabic term called al-jabr, or "reunification," which translates as "to reunite or put back together again," used specifically to refer to moving terms to eliminate negatives, forming the basis of systematic equation solving. First introduced by Persian mathematician Muhammad ibn Musa al-Khwarizmi's influential book, Al-Kitab al-Mukhtasar fi Hisab al-Jabr Wal Muqabala," or "The Compendious Book on Calculation by Completion and Balancing," al-Khwarizmi provided methods of solving equations through balancing and rearrangement, which laid the basis for modern algebraic mathematics and founded it upon.

History

The Origin of Algebra

Algebra dates back to ancient Babylonia, Egypt, Greece, China, and India, where early attempts at solving mathematical issues involving unknown quantities began to surface. Egypt produced its Rhind Mathematical Papyrus (1650 BCE), detailing solutions for linear equations. Babylonian clay tablets contain information such as methods for completing squares. Diophantus' work "Arithmetica," published during the 3rd century CE by Greek mathematicians like him, influenced medieval Arabic algebra significantly. Al-Khwarizmi laid the groundwork in 825 CE for manipulating linear and quadratic equations using symbolic notation, while subsequent Indian mathematicians such as Brahmagupta contributed further methods and techniques, while Europeans such as Viete and Descartes created modern symbolic notation systems, such as scientific notation.

The Emergence of Abstract Algebra

Abstract algebra has evolved throughout history into its modern manifestation: groups, rings, and fields are now studied using abstract algebra techniques. Algebraic geometry focuses on understanding the principles and properties that underlie structures rather than simply solving equations; mathematicians such as Evariste Galois and Emmy Noether were pioneers in creating such advanced concepts. Galois introduced group theory, which helps explain symmetries of algebraic equations, while Emmy Noether's work on rings and fields provided us with deeper insights into their properties and relationships.

The Algebraization of Mathematics

At some point during the mid-19th century, algebra changed course from its study of polynomials towards exploring generalized algebraic structures—heralding its transformation into abstract algebra. This discipline studies the axiomatic bases for different algebraic operations that lead to systems like Boolean algebra, vector algebra, and matrix algebra. Mathematicians such as David Hilbert, Ernst Steinitz, Emmy Noether, and Emil Artin made significant advances in classifying algebraic structures as groups, rings, or fields. Alfred North Whitehead's 1898 work on universal algebra laid the groundwork, upon which Garrett Birkhoff expanded in the 1930s—leading him eventually to apply algebraic methods throughout mathematics, leading eventually to fields such as topological algebra, homological algebra, and category theory.

Basic Concepts of Algebra

Algebraic Terms

Variables, Operators, Constants, Arithmetic Operations

Variables represent unknown quantities and are commonly denoted by symbols like \(x\) and \(y\). Operators are mathematical symbols such as \(+\), \(-\), \(\times\), and \(\div\), which signify addition, subtraction, multiplication, and division, respectively. Constants are fixed values that remain unchanged, such as 3 or -7.

Operations with Algebraic Terms

Simplifying algebraic terms involves performing arithmetic operations and combining like terms. This includes adding and subtracting terms with the same variable, multiplying and dividing coefficients, and using the distributive property. For instance, in the expression \(3x + 2x - 5\), the like terms \(3x\) and \(2x\) can be combined to simplify it to \(5x - 5\).

Algebraic Expressions

Monomials

Monomials are single-term algebraic expressions containing constants or variables without addition or subtraction operations—for instance, \(5x\), \(3a^2\), and 7 are examples. They represent some of the simplest algebraic expressions.

Polynomials

Polynomials are algebraic expressions consisting of multiple monomials added or subtracted, such as \(2x^2 + 3x + 1\) or \(4a^3 - 2a + 5\). The degree is determined by the highest exponent.

Algebraic Equations

Linear Equations

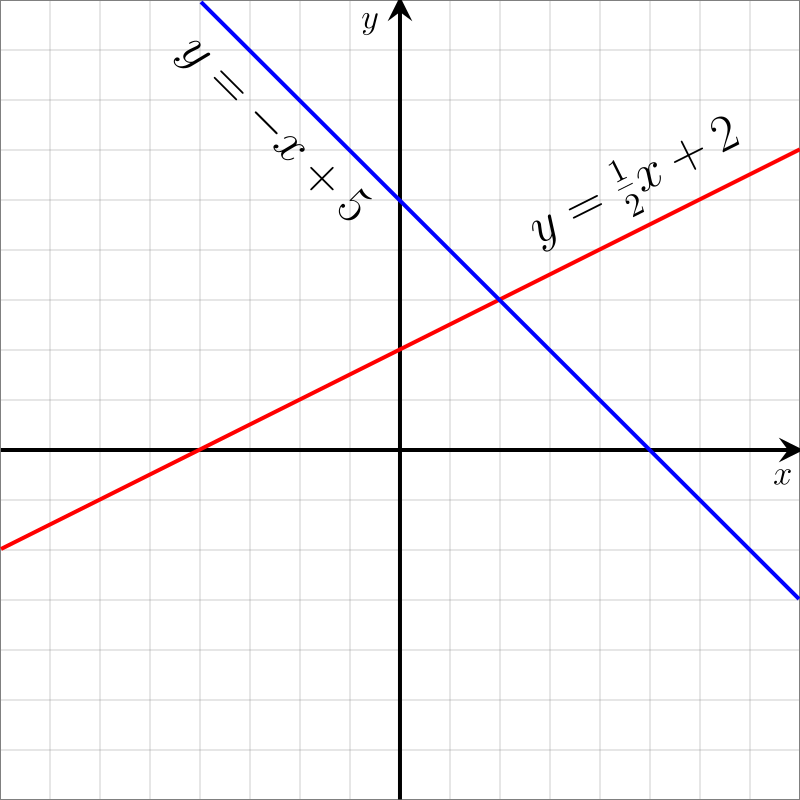
Linear equations are first-degree equations where the highest power of the variable is one. They take the form \(ax + b = c\), with \(a\), \(b\), and \(c\) as constants and \(x\) as the variable. For example, in \(2x + 3 = 7\), solving for \(x\) involves isolating the variable, resulting in \(x = 2\). Linear equations represent straight lines on a coordinate plane and are fundamental in various applications.

Quadratic Equations

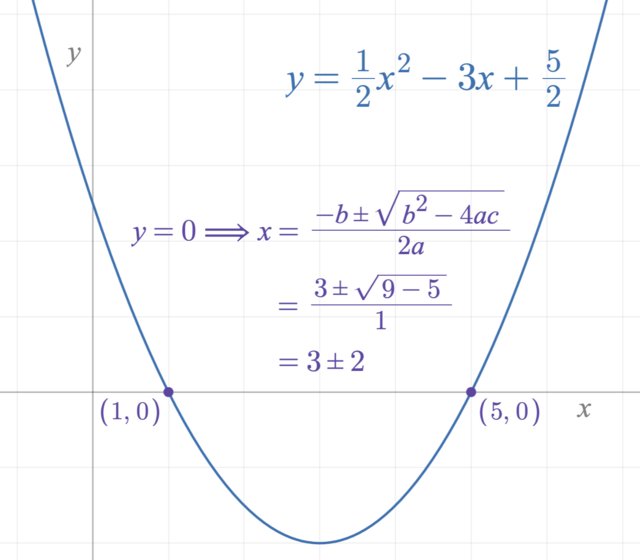
Quadratic equations are second-degree equations featuring a squared variable (\(x^2\)). They take the form \(ax^2 + bx + c = 0\), with \(a\), \(b\), and \(c\) as constants. An example is \(x^2 - 4x + 4 = 0\). Solving methods include factoring, completing the square, and the quadratic formula \(\left( x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \right)\). Quadratic equations graph as parabolas and are essential in fields like physics, engineering, and economics for modeling and solving various real-world problems.

Functions

Exponents

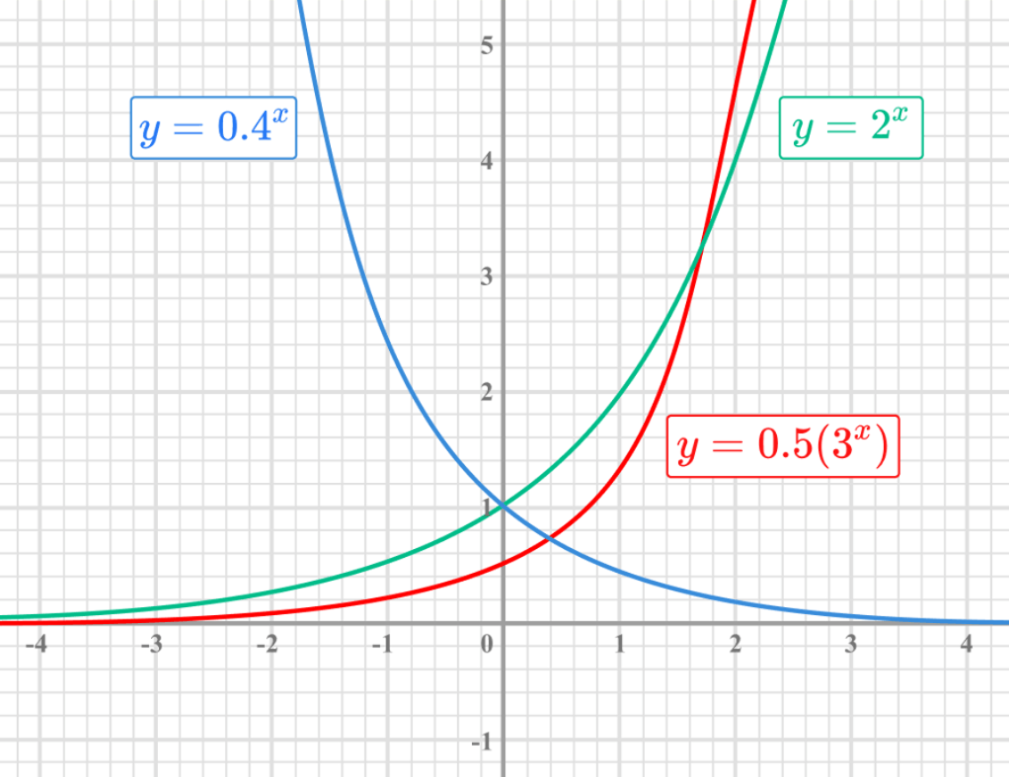
Exponential functions involve expressions where a constant base is raised to a variable exponent. In these functions, the variable \(x\) appears in the exponent, and the base can be any positive number. For instance, in the function \(2^x\), the base 2 indicates that the output doubles with each increase in \(x\). Similarly, \(e^x\) involves the natural exponential base \(e\), approximately equal to 2.718, and is widely used in calculus and natural logarithms.

Logarithms

Logarithmic functions are the inverse of exponential functions and provide a way to solve for the exponent in an equation involving exponentiation. A common logarithmic function is \(\log(x)\), where the base 10 is implied, and \(x\) is the input. The natural logarithm, denoted as \(\ln(x)\), has the base \(e\). Logarithms answer the question: "To what exponent must the base be raised to obtain \(x\)?" For example, \(\log_{10}(100) = 2\)  because \(10^2 = 100\).

Branches of Algebra

Pre-algebra 

Pre-algebra provides essential mathematical concepts necessary for comprehending algebra. The course covers fundamental operations involving addition, subtraction, multiplication, and division utilizing whole numbers, fractions, and decimals, as well as variable manipulation to manipulate simple algebraic expressions and solve equations. Students gain essential preparation needed for more advanced subjects like algebra and calculus as well as future applications of math, such as studies or applications, by participating in pre-algebra courses such as this one.

Elementary Algebra

Elementary algebra builds upon pre-algebra by delving deeper into its fundamental principles, covering topics like solving linear equations and inequalities, working with polynomials, understanding factors and multiples, graphing linear equations with slope intercepts or intercepts for interpretation, solving systems of equations using substitution or elimination, and quadratic equations/factoring/quadratic formulas that help prepare students for more challenging mathematical courses such as geometry/Algebra II.

Linear Algebra

Linear algebra provides its students with a foundation of vector spaces, linear transformations, and matrices in which to study vector addition and multiplication; linear transformations allow vectors to map onto other vectors linearly; matrices offer representation for these transformations with key concepts like determinants, eigenvalues, and eigenvectors discussed during classes.

Abstract Algebra

Abstract algebra (also referred to as modern algebra) studies algebraic structures like groups, rings, and fields. Unlike elementary or linear algebra, abstract algebra takes an overall view when studying these structures by comparing various structures with each other and their properties. Algebraic structures provide the framework for operations on mathematical objects, whereas groups, rings, and fields differ by using various operations and obeying laws governed by these structures—usually abstract algebra is considered advanced undergraduate coursework for mathematics majors who have completed linear algebra as part of their major studies.

Algebraic Formulas

Properties of Algebra

Algebra offers several fundamental properties that are used to simplify and manipulate algebraic expressions and make math problems simpler to comprehend and solve. Some of these properties include:

1. Additive Inverse Property:

Any number added to its inverse equals zero: \(a + (-a) = 0\).

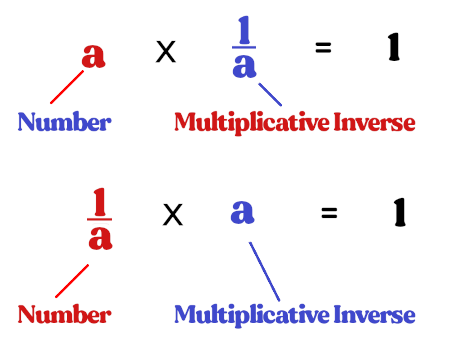
2. Multiplicative Inverse Property:

Any number multiplied by its reciprocal equals one: \(a \cdot \frac{1}{a} = 1\) for \(a \neq 0\).

3. Additive Identity Property:

The sum of any number and zero is the number itself: \(a + 0 = a\).

4. Multiplicative Property of Zero:

The product of any number and zero is zero: \(a \cdot 0 = 0\).

Operational Rules of Algebra

Operational rules such as PEMDAS/BODMAS or properties of equality such as transitive, reflexive, or symmetric provide guidance for solving algebraic expressions and equations correctly in sequence and method. There are common operational rules as follows:

1. Associative Property:

The way numbers are grouped in addition or multiplication does not change the result: \((a + b) + c = a + (b + c)\) and \((ab)c = a(bc)\).

2. Commutative Property:

The order in which numbers are added or multiplied does not affect the outcome: \(a + b = b + a\) and \(ab = ba\).

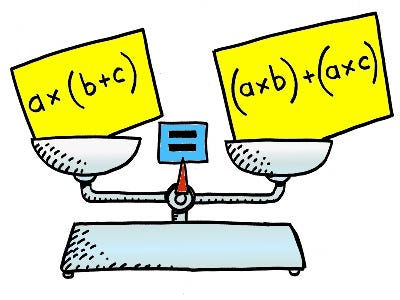
3. Distributive Property:

Combination of addition and multiplication: \(a(b + c) = ab + ac\).

Basic Formulas

Basic algebraic formulas are essential tools for solving equations and simplifying expressions. These include:

1. Difference of Squares:

\(a^2 - b^2 = (a + b)(a - b)\), which simplifies the expression of a squared term subtracted by another squared term.

2. Perfect Square Trinomial:

\((a + b)^2 = a^2 + 2ab + b^2\), which expands the square of a binomial into a trinomial.

3. Sum of Cubes:

\(a^3 + b^3 = (a + b)(a^2 - ab + b^2)\), an identity used to factorize the sum of two cubed terms.

4. Binomial Theorem:

\((a + b)^n\), which expands a binomial raised to any positive integer power \(n\) into a sum involving terms of the form \(\binom{n}{k} a^{n-k} b^k\).

Applications of Algebra

Algebraic Applications in Physics

In physics, algebra is fundamental for formulating and solving equations that describe various natural phenomena. For instance, Newton's second law of motion \((F = ma)\) uses algebra to relate force, mass, and acceleration. Similarly, Einstein's energy-mass equivalence formula \((E = mc^2)\) utilizes algebra to express the relationship between energy, mass, and the speed of light. Algebraic equations help physicists understand and quantify the relationships between different physical quantities, such as velocity, time, distance, and force. What’s more, physicists can predict the outcomes of experiments, model complex systems, and develop new theories with the help of algebra.

Algebraic Applications in Medicine

Algebraic analysis in medicine is indispensable for many tasks, such as dosage calculations, unit conversions, and statistical data analysis. Algebraic equations play an essential role in unit conversion between measurement systems to ensure accurate drug administration, while algebraic models in medical research simulate disease spread and assess the efficacy of treatments, providing researchers with tools for predictions, intervention design, testing of hypotheses, and improving patient outcomes by offering quantitative tools for analyzing clinical data and testing hypotheses.

reference：

https://wagner.nyu.edu/files/students/Math_Review_-_Algebra_Operations.pdf

https://uwaterloo.ca/pure-mathematics/about-pure-math/what-is-pure-math/what-is-algebra

https://www.niu.edu/mathmatters/everyday-life/index.shtml