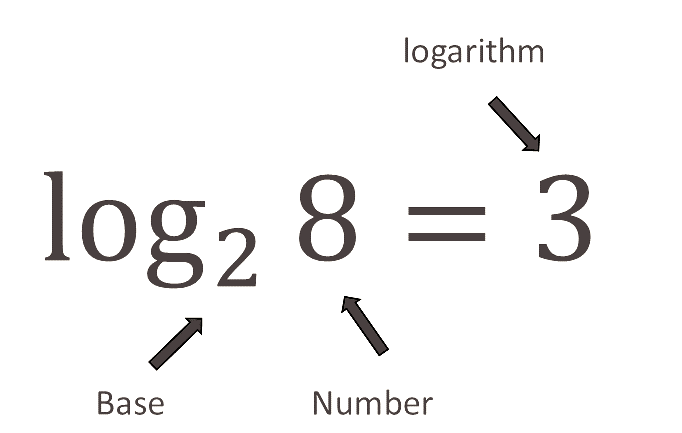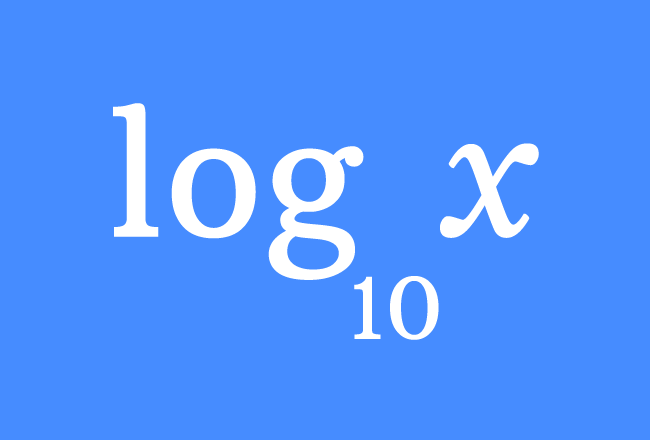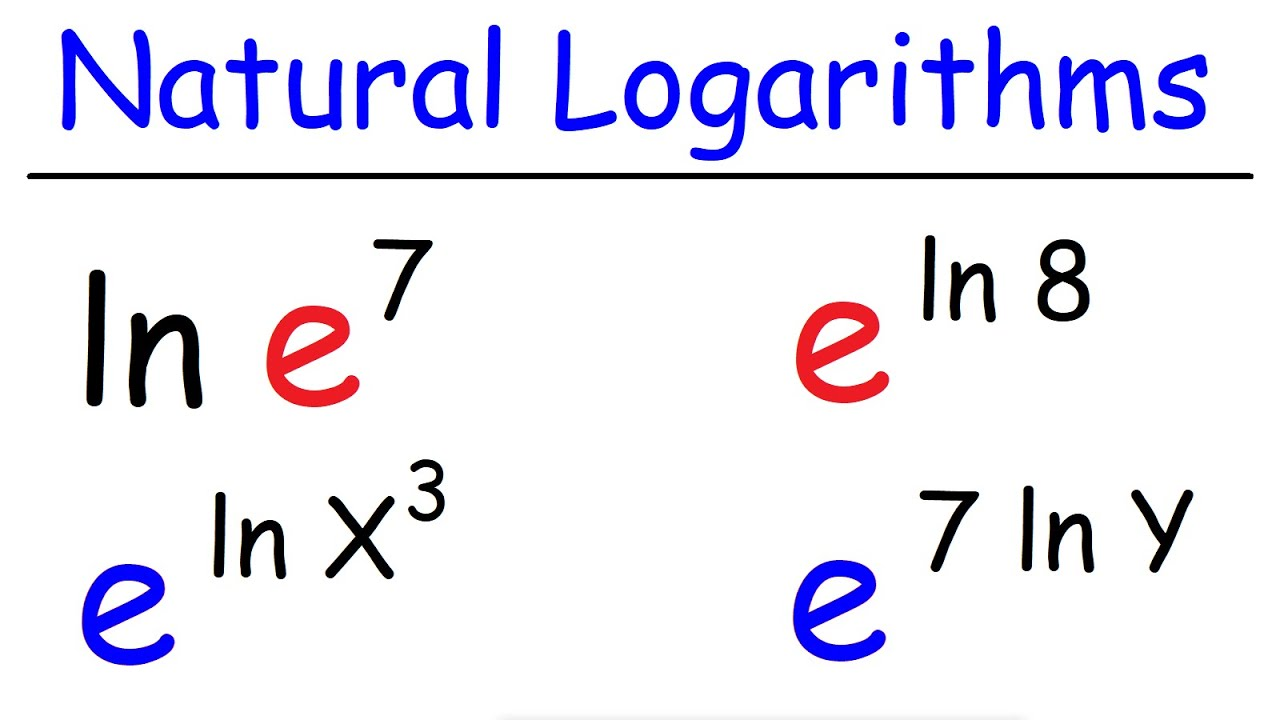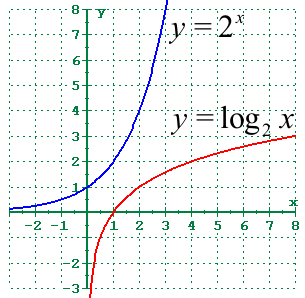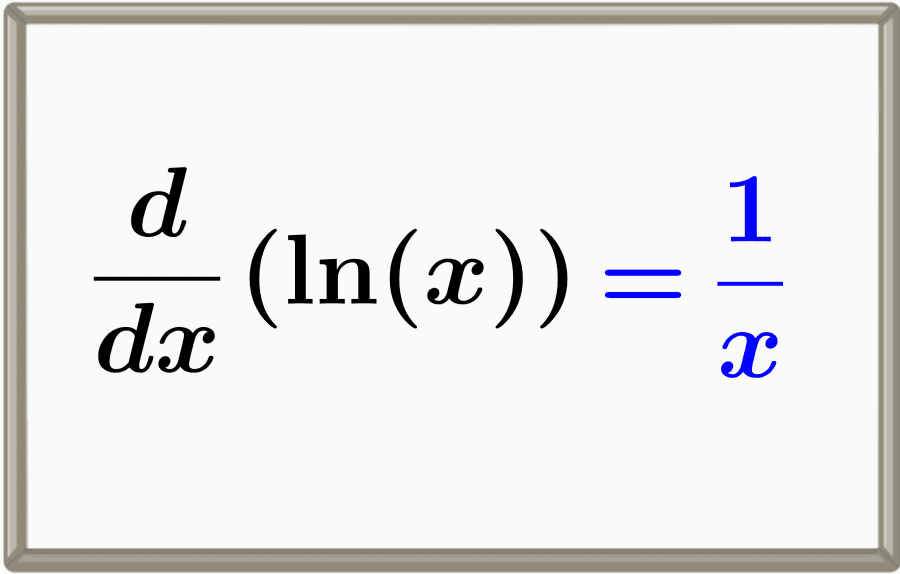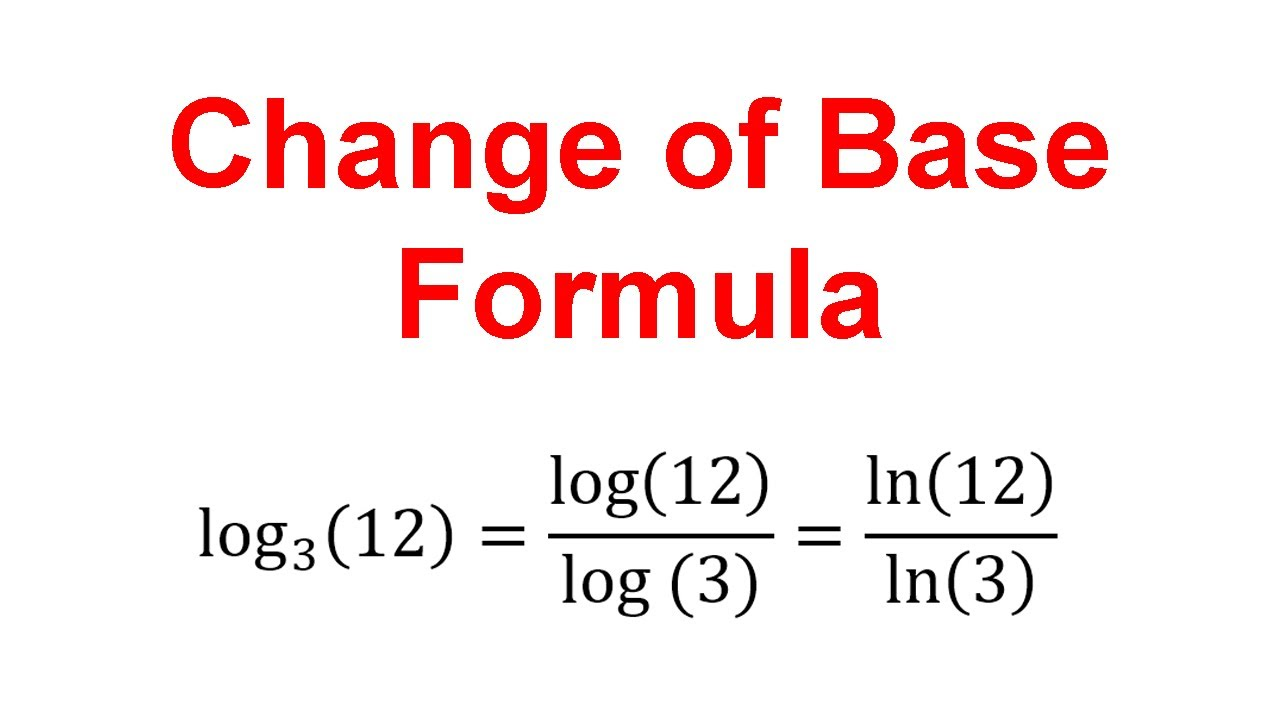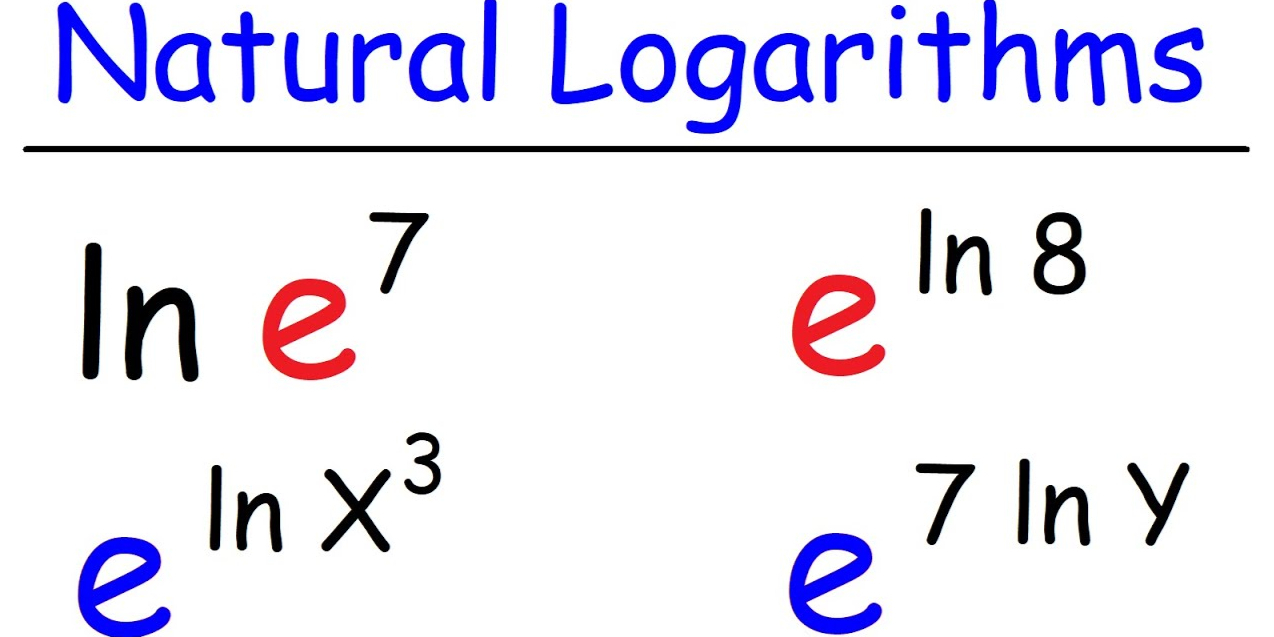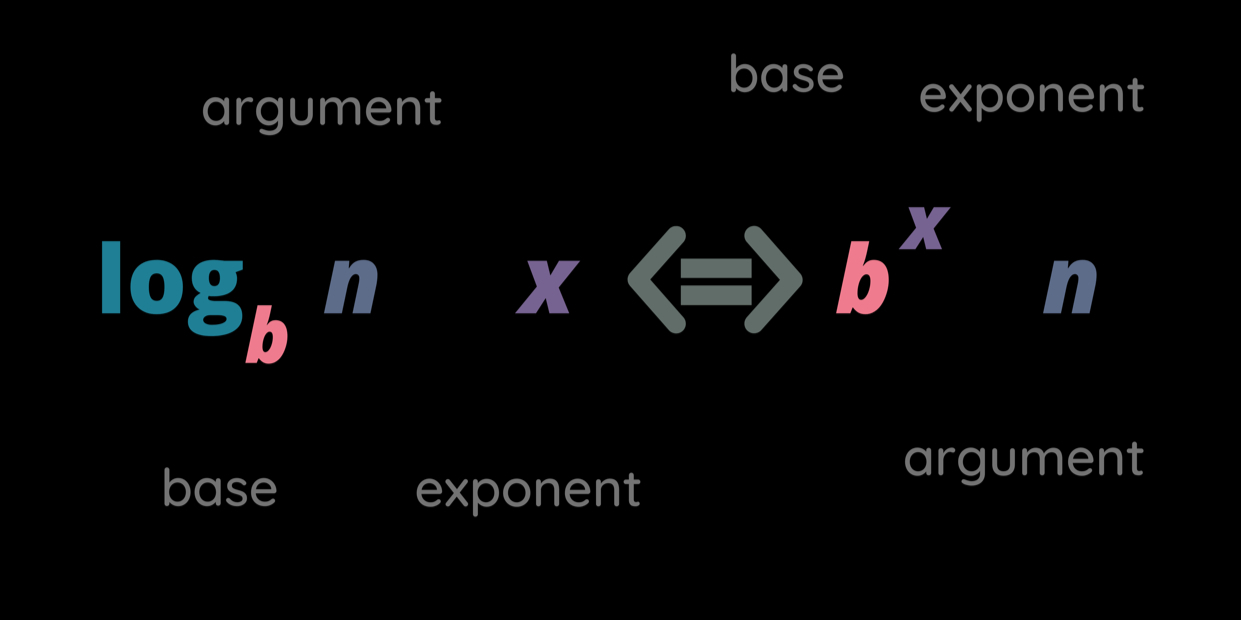What Are Logarithmic Functions?

Definition and Origin of Logarithmic Functions

Core Definition of Logarithms

Logarithms are functions that reverse exponential operations; that is, they reverse exponential operations and represent negative exponential operations. The general form of a logarithmic function is expressed as: 

\(\log_b(x) = y \iff b^y = x,\)

where \(b > 0\), \(b \neq 1\), and \(x > 0\). In this equation, \(b\) is referred to as the base of the logarithm. The value \(y\) denotes the exponent or power to which the base \(b\) is raised in order to produce \(x\). For example, since \(2^3 = 8\), it follows that \(\log_2(8) = 3\).

The logarithmic function effectively reverses the role of the exponential function, making it an essential mathematical tool. Logarithms can be used to simplify complex multiplication and division into addition and subtraction. The formula for changing the base of a logarithmic function is also useful when switching from one base to another:

\(\log_b(x) = \frac{\ln(x)}{\ln(b)},\)

where \(\ln(x)\) is the natural logarithm, with \(e\) (\(e \approx 2.718\)) as its base.

Historical Background of Logarithms

The concept of logarithms was introduced in the early 17th century by John Napier, a Scottish mathematician. He published logarithmic tables in 1614 to aid in simplifying tedious mathematical computations. Napier's work provided astronomers, physicists, and engineers with a powerful tool to perform calculations more efficiently during an era when computation was performed manually.

Logarithms' historical significance lies in their ability to transform multiplication and division into addition and subtraction, using the property:

\(\log_b(x \times y) = \log_b(x) + \log_b(y).\)

For example, calculating \(1,000 \times 50,000\) manually could be cumbersome, but logarithmic tables simplified this into addition:

\(\log_{10}(1,000) + \log_{10}(50,000).\)

Logarithmic functions laid the foundation for computational techniques used in various fields, such as navigation, astronomy, and engineering. Before the advent of calculators and computers, tools such as the slide rule relied on logarithmic scales for rapid calculations, significantly advancing scientific and industrial progress during the 18th and 19th centuries.

Types of Logarithmic Functions

Common Logarithm

The common logarithm, denoted as \(\log(x)\), is a logarithm with base 10. For example:

\(\log_{10}(1000) = 3 \quad \text{because} \quad 10^3 = 1000.\)

The base-10 logarithm is prevalent in many real-world applications, particularly in scientific fields. One prominent example is the Richter scale, which measures the magnitude of earthquakes. On this logarithmic scale, each whole number increase corresponds to a tenfold increase in earthquake amplitude:

\(\text{Magnitude} = \log_{10}\left(\frac{I}{I_0}\right),\)

where \(I\) is the measured seismic intensity and \(I_0\) is a reference value.

Another application of common logarithms appears in chemistry, specifically the pH scale that measures the acidity of a solution:

\(\text{pH} = -\log_{10}[\text{H}^+],\)

where \([\text{H}^+]\) represents the hydrogen ion concentration.

Natural Logarithm

The natural logarithm, represented as \(\ln(x)\), uses the base \(e\) (\(e \approx 2.718\)), a fundamental constant in mathematics. For example:

\(\ln(e^2) = 2.\)

Natural logarithms are widely used to model continuous growth or decay in mathematics, economics, biology, and other disciplines. The connection between natural logarithms and exponential growth arises from equations such as \(P(t) = P_0 e^{rt}\), which describe population growth, radioactive decay, or interest calculations. Solving for time \(t\) in these equations often requires the natural logarithm.

For example, in compound interest, where a principal \(P_0\) grows exponentially over time, the time required to double the investment can be calculated using \(\ln(2)\):

\(t = \frac{\ln(2)}{r},\)

Where \(r\) is the annual growth rate.

Specialized Logarithms

Apart from the common and natural logarithms, other logarithmic functions are used in specialized areas:

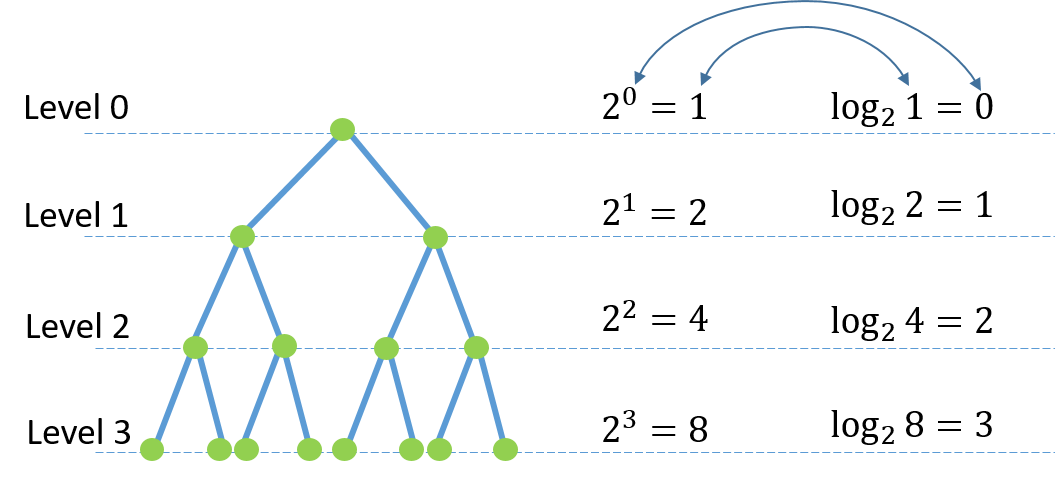
- Binary Logarithm: \(\log_2(x)\), which uses base 2, is common in computer science to measure data size or algorithm efficiency.

- Customized Logarithms: Certain fields apply logarithms tailored to their unique needs. For instance, the stellar magnitude scale in astronomy is logarithmic, capturing how the human eye perceives differences in brightness.

In data science, logarithms are critical for scaling and normalizing large datasets. The "logarithmic transformation" can reduce skewness, making data more interpretable in visualization and statistical models.

Properties and Rules of Logarithmic Functions

Fundamental Properties

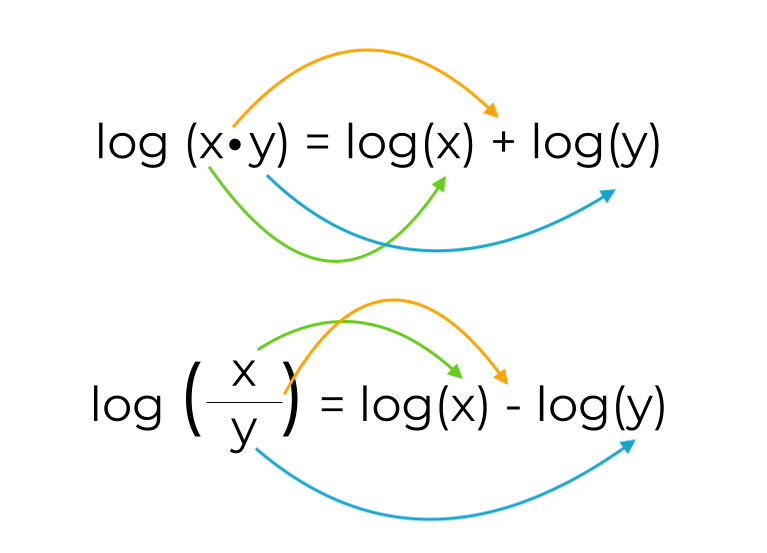
Logarithmic functions obey several essential properties that simplify operations:

Product Rule:

\(\log_b(xy) = \log_b(x) + \log_b(y).\)

For example: \(\log_2(8 \times 4) = \log_2(8) + \log_2(4) = 3 + 2 = 5.\)

Quotient Rule:

\(\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y).\)

For example: \(\log_3\left(\frac{81}{27}\right) = \log_3(81) - \log_3(27) = 4 - 3 = 1.\)

Power Rule:

\(\log_b(x^r) = r \cdot \log_b(x).\)

For example: \(\log_2(8^2) = 2 \cdot \log_2(8) = 2 \cdot 3 = 6.\)

These properties are widely used to simplify calculations in both theoretical mathematics and practical applications.

Relationship Between Logarithms and Exponentials

Logarithmic functions and exponential functions are inverse operations. For example:

\(b^{\log_b(x)} = x \quad \text{and} \quad \log_b(b^x) = x.\)

This relationship forms the basis of their use in solving exponential equations. For instance, given \(10^x = 500\), we solve for \(x\) using:

\(x = \log_{10}(500).\)

This example illustrates how logarithms are indispensable tools in various domains.

Misconceptions About Logarithms

It is essential to note limitations or misconceptions associated with logarithms. For instance:

\(\log_b(x + y) \neq \log_b(x) + \log_b(y),\)

and

\(\log_b(x - y) \neq \log_b(x) - \log_b(y).\)

Mistaken application of these properties can lead to errors in mathematical problem-solving. For example, \(\log_{10}(2 + 3) \neq \log_{10}(2) + \log_{10}(3)\). Correct use is vital to ensure accurate outcomes.

Graph and Geometric Characteristics of Logarithmic Functions

Characteristics of the Graph

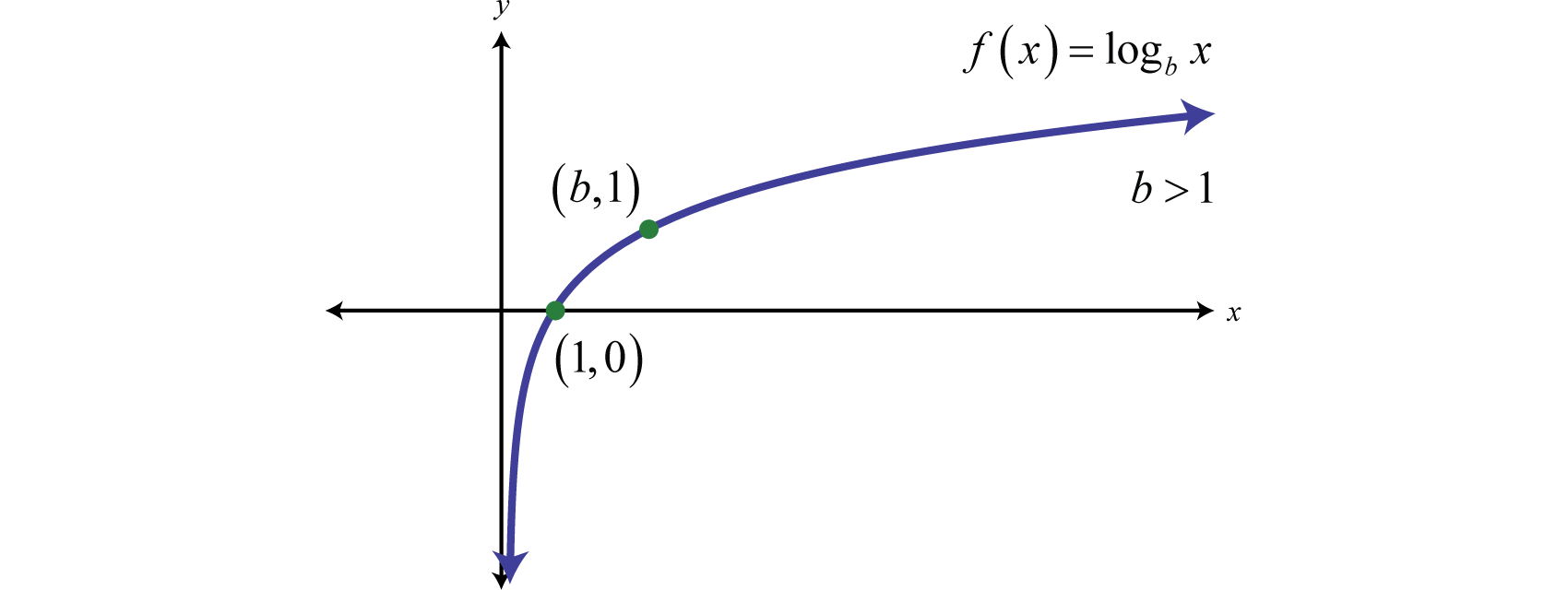
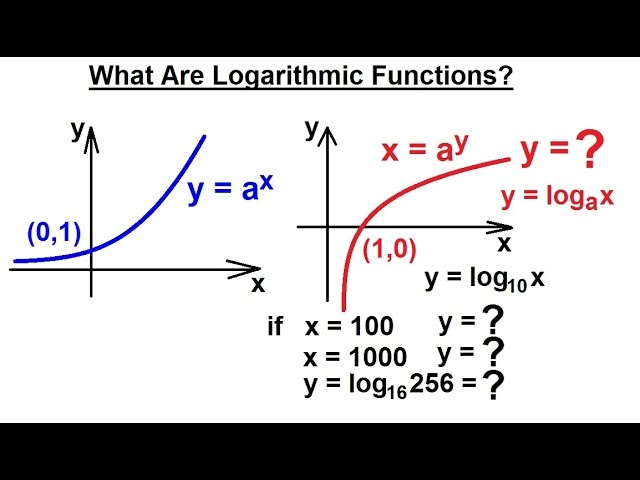
The graph of a logarithmic function offers important insights into its behavior. For a logarithmic function of the form \(\log_b(x)\), the following characteristics hold:

The domain of a logarithmic function is limited to positive real numbers, where \(x > 0\). This restriction arises because logarithms are undefined for non-positive values of \(x\). For example, \(\log_b(-1)\) does not exist in the real number system.

Range

The range of a logarithmic function consists of all real numbers, \((-\infty, +\infty)\). This means a logarithmic function can output any real value. For example,\(\log_2(1/2) = -1\), and \(\log_2(8) = 3\).

Vertical Asymptote

The graph of \(\log_b(x)\) has a vertical asymptote at \(x = 0\). As \(x\) approaches zero from the right, the function tends toward negative infinity.

Intercept

For \(\log_b(x)\), the intercept on the \(x\)-axis occurs at \(x = 1\), because \(\log_b(1) = 0\).

For example, the graph of \(\log_{10}(x)\) starts near negative infinity as \(x\) approaches 0 from the right, passes through (1, 0), and increases steadily while flattening for larger \(x\).

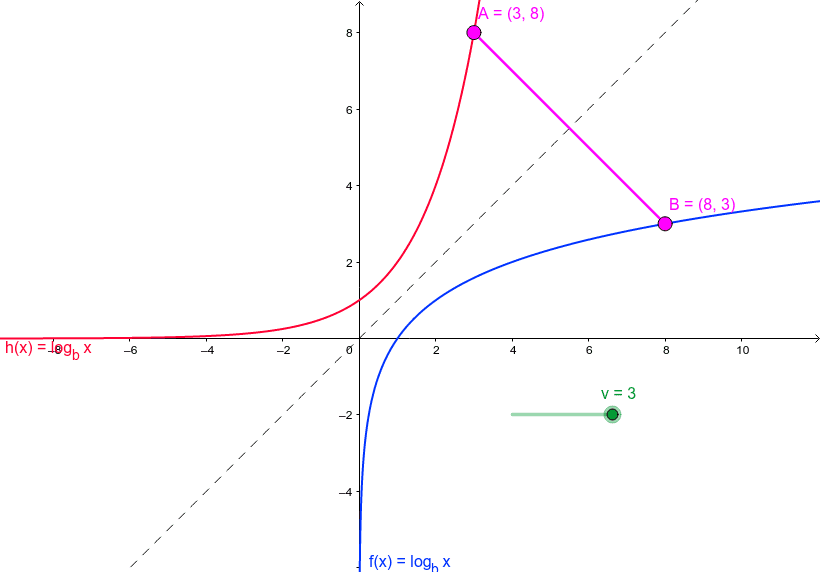
Symmetry with Exponential Functions

Logarithmic and exponential functions are reflections of one another across the line \(y = x\). The essence of this symmetry lies in their inverse relationship. Mathematically:

\(f(x) = b^x \quad \text{and} \quad g(x) = \log_b(x),\)

result in \(f(g(x)) = x\) and \(g(f(x)) = x\). This symmetry is visually significant, as the exponential curve is increasing steeply while the logarithmic curve grows gradually.

This inverse relationship is fundamental to numerous applications, including solving equations involving compound growth or exponential decay. For instance, solving \(2^x = 32\) requires finding \(x = \log_2(32) = 5\), effectively reversing the exponential process.

Trends in Logarithmic Graphs

The logarithmic graph grows indefinitely but at a decreasing rate. This gradual growth rate makes logarithms suitable for applications where relative differences matter more than absolute values. Examples include audio decibel levels and the pH scale in chemistry, where logarithmic scaling simplifies the representation of large dynamic ranges.  

Applications of Logarithmic Functions

Real-World Scientific Applications

Logarithmic functions find extensive usage in science and engineering due to their ability to compress large ranges of values into manageable scales.

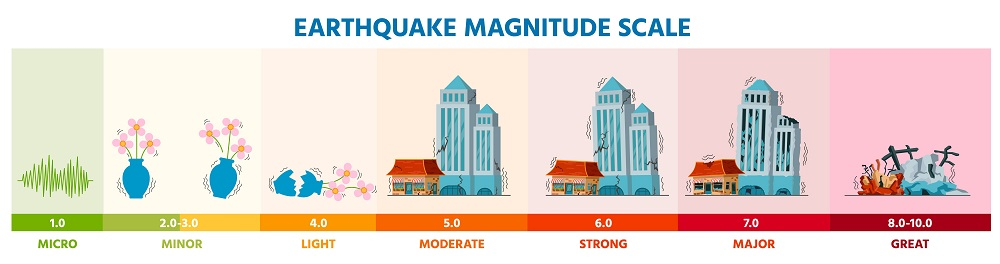
Earthquake Magnitude (Richter Scale)

The magnitude \(M\) of an earthquake is calculated using the logarithmic Richter scale:

\(M = \log_{10}\left(\frac{I}{I_0}\right),\)

where \(I\) represents the intensity of the earthquake, and \(I_0\) is a reference intensity. For instance, an earthquake with \(I = 10,000 \cdot I_0\) has a magnitude of \(\log_{10}(10,000) = 4\).

Chemistry (pH Scale)

To indicate the acidity or alkalinity of a solution, the pH scale utilizes a logarithmic scale:

\(\text{pH} = -\log_{10}[\text{H}^+],\)

where \([\text{H}^+]\) is the molar hydrogen ion concentration. For instance, a solution with \([\text{H}^+] = 10^{-3}\) mol/L has a pH of \(3\). The logarithmic nature of the pH scale compresses the wide range of hydrogen ion concentrations into a limited scale from 0 to 14.

Radioactive Decay

Logarithmic functions model the time it takes for radioactive substances to decay. The equation describing the decay is related to the natural logarithm:

\(N(t) = N_0 e^{-kt}, \quad \ln\left(\frac{N_0}{N(t)}\right) = kt,\)

where \(N(t)\) is the quantity remaining at time \(t\), \(N_0\) is the initial quantity, and \(k\) is the decay constant.

Logarithms in Data Science and Technology

Data Transformation and Compression

Logarithmic transformations can help data science practitioners deal with unbalanced datasets by normalizing outliers, controlling variance and lessening outliers - this technique has proved particularly helpful when studying wealth distribution studies where income range from hundreds to billions and requires logarithm transformation to present data graphically more clearly.

Algorithm Efficiency

The logarithm base-2, \(\log_2(x)\), plays a vital role in computational complexity analysis. Sorting algorithms, such as QuickSort and MergeSort, operate with logarithmic efficiency, denoted as \(O(n \log_2(n))\).

Search Algorithms and Binary Trees

Binary search, which divides data into halves, runs in \(O(\log_2(n))\) time complexity. In computer science, logarithmic structures like binary search trees ensure efficient storage and retrieval of data.

Human Perception and Psychology

The human sensory system often operates on a logarithmic scale rather than a linear one:

Sound Intensity (Decibel Scale)

The relative intensity of sound is measured in decibels (dB), which uses a logarithmic scale:

\(\text{dB} = 10 \cdot \log_{10}\left(\frac{I}{I_0}\right),\)

where \(I\) denotes the sound intensity, and \(I_0\) is a reference intensity. For example, a 100-fold increase in sound intensity corresponds to \(10 \cdot \log_{10}(100) = 20 \, \text{dB}\).

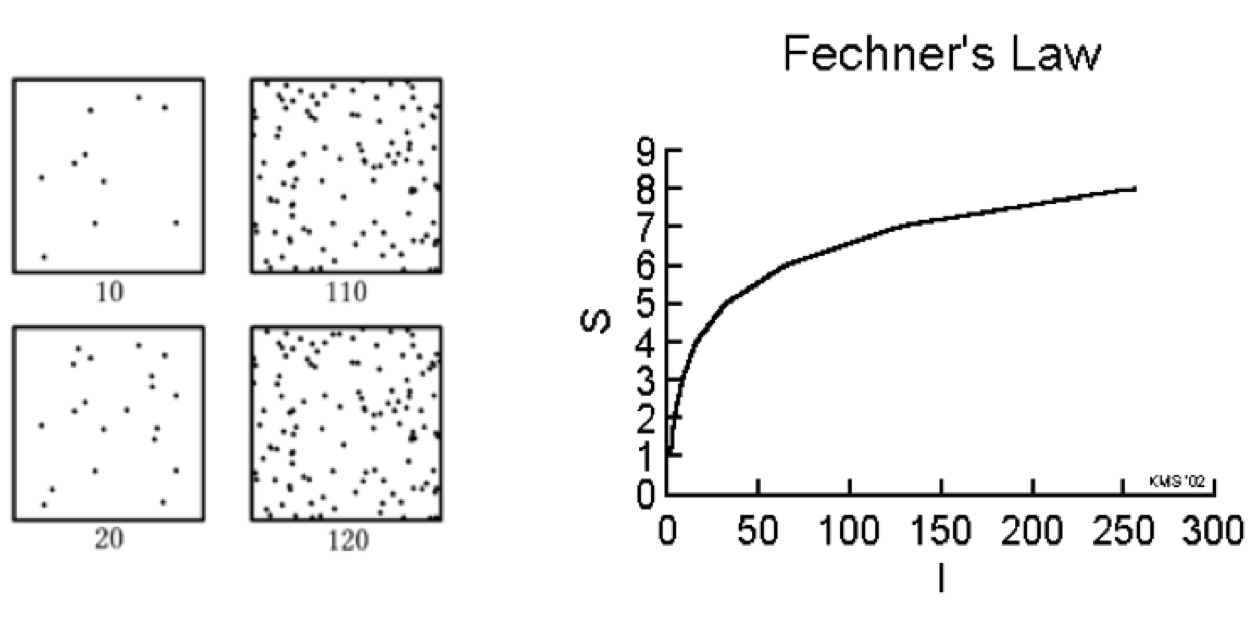
Fechner's Law in Psychology

Fechner's Law posits that the perceived intensity of a stimulus grows logarithmically with its actual magnitude. For instance, doubling the brightness of a light source does not result in a doubling of its perceived intensity.

Interdisciplinary Connections of Logarithmic Functions

Relation to Calculus

Logarithmic functions are closely tied to calculus, particularly in differentiation and integration:

Derivative of Natural Logarithm

\(\frac{d}{dx} \ln(x) = \frac{1}{x}, \quad \frac{d}{dx} \log_b(x) = \frac{1}{x \ln(b)}.\)

For example, the derivative of \(\ln(5x)\) is:

\(\frac{d}{dx} \ln(5x) = \frac{1}{5x} \cdot 5 = \frac{1}{x}.\)

Integration

The integral of the natural logarithm is given by:

\(\int \ln(x) \, dx = x \ln(x) - x + C.\)

This result often appears in problems involving logarithmic functions in growth or decay contexts.

Use in Complex Analysis

In complex analysis, logarithms extend beyond the real line to the complex plane. A key relationship is expressed as:

\(\ln(z) = \ln|z| + i\arg(z),\)

where \(z\) is a complex number, \(\ln|z|\) is the natural logarithm of the modulus, and \(\arg(z)\) is the argument of \(z\).

Logarithms in the complex plane exhibit periodicity, with multiple "branches" due to the repeating nature of the argument \(\arg(z)\). This makes logarithms essential in fields like signal processing and wave mechanics.

Techniques for Calculating Logarithmic Values

Precise Calculation Methods

Calculating logarithmic values often relies on either estimation techniques or exact solutions using calculators or logarithmic tables. For certain values of \(x\), logarithms can be calculated directly:

For Exact Powers of the Base

Logarithms are straightforward to compute when \(x\) is an exact power of the base. For example:

\(\log_2(32) = 5 \quad \text{because} \quad 2^5 = 32.\)

Natural Logarithms of \(e^n\)

\(\ln(e^4) = 4 \quad \text{and} \quad \ln(1) = 0.\)

These direct calculations are foundational in mathematics and appear frequently in various applications.

Change of Base Formula

When the base of the logarithm is not convenient, the change of base formula can be used:

\(\log_b(x) = \frac{\log_k(x)}{\log_k(b)},\)

where \(k\) is any positive number, commonly \(10\) or \(e\).

For example, to calculate \(\log_2(50)\):

\(\log_2(50) = \frac{\ln(50)}{\ln(2)}.\)

Here, using a calculator:

\(\ln(50) \approx 3.912 \quad \text{and} \quad \ln(2) \approx 0.693,\)

So:

\(\log_2(50) = \frac{3.912}{0.693} \approx 5.64.\)

The change of base formula is particularly useful in fields like computer science, where binary logarithms (\(\log_2\)) are often needed but not natively supported by standard calculators.

Mental Math and Approximation Techniques

For practical purposes, particularly when exact values are unnecessary, approximate techniques can be applied to calculate logarithmic values:

Logarithm of Numbers Near Powers of the Base

Numbers close to the power of the base can be approximated by recognizing their deviation. For example:

\(\log_{10}(120) \approx \log_{10}(100) + \log_{10}(1.2).\)

Since \(\log_{10}(100) = 2\) and \(\log_{10}(1.2) \approx 0.08\):

\(\log_{10}(120) \approx 2.08.\)

Using Rough Benchmarks

For base 2, benchmarks include:

\(\log_2(1) = 0, \quad \log_2(2) = 1, \quad \log_2(4) = 2, \quad \log_2(8) = 3.\)

To approximate \(\log_2(20)\):

Recognize \(16 < 20 < 32\), so \(4 < \log_2(20) < 5\). Using linear interpolation gives a closer estimate of approximately \(4.32\).

Taylor Series Expansion

For values close to 1, the natural logarithm can be approximated using:

\(\ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots.\)

For example, for \(x = 0.1\):

\(\ln(1.1) \approx 0.1 - \frac{0.1^2}{2} + \frac{0.1^3}{3} = 0.1 - 0.005 + 0.000333 = 0.095333.\)

These techniques enable quick calculations and estimations, especially in fields where logarithmic values are computed frequently without the need for high precision.

Future Directions and Impact of Logarithmic Functions

Data Security and Encryption

Logarithmic functions are critical for modern encryption methods and data security. For example, the Diffie-Hellman key exchange protocol relies on the difficulty of solving discrete logarithms in finite fields for secure data transfer. The underlying computation involves solving equations of the form:

\(g^x \mod p,\)

where the inverse operation (computing \(x\)) is infeasible without significant computational resources.

As computational power grows, researchers are exploring logarithms and their extensions in quantum cryptography, ensuring secure communication in the era of quantum computing.

Use in Climate Science and Modeling

Logarithmic functions play a vital role in understanding and predicting changes in Earth's climate. For instance:

CO\(_2\) Concentration and Radiative Forcing

The relationship between atmospheric CO\(_2\) concentrations and Earth's radiative forcing follows a logarithmic model:

\(\Delta F = \alpha \cdot \ln\left(\frac{C}{C_0}\right),\)

where \(C\) is the current CO\(_2\) level, \(C_0\) is the pre-industrial level, and \(\alpha\) is a constant.

Risk Assessments and Log Scales

Logarithmic functions help scientists visualize risks and thresholds for tipping points, as small exponential changes in greenhouse gases can have logarithmic effects on temperature rise.

Extending Logarithms to Emerging Fields

Artificial Intelligence and Efficiency Scaling

Logarithmic functions are often used to model the diminishing returns of neural network performance as model size grows. For instance, doubling the number of parameters in a deep learning model improves accuracy logarithmically, highlighting trade-offs in resource allocation.

Quantum Information Science

In quantum mechanics, the logarithm of probability amplitudes is applied in entropy measurements, such as the von Neumann entropy:

\(S = -\text{Tr}(\rho \ln(\rho)),\)

Where \(\rho\) is the density matrix of a quantum state. This application demonstrates the deep connection between logarithms and information theory.

Economic and Financial Modeling

Logarithmic functions form the backbone of economic models like utility theory, which measures human satisfaction logarithmically relative to resource consumption. This insight supports sustainable growth initiatives by emphasizing relative rather than absolute gains.

Conclusion

Logarithmic functions occupy an invaluable place in mathematics and its applications, serving a multitude of disciplines from sciences such as biology to engineering and technology. Their properties - which range from turning multiplication into addition, simplifying scales, and modeling growth - make logarithmic functions indispensable tools across science, engineering, and technology applications. From explaining natural phenomena like exponential decay to driving advances in encryption and AI research, logarithmic functions reveal both abstraction and real-world application while at once showing their mathematical elegance by acting as bridges between various fields while opening new avenues enabling innovations that shape both our understanding of world history as well as shaping its future development.

Reference:

https://www.britannica.com/science/Richter-scale

https://www.bigocheatsheet.com/

https://rss.onlinelibrary.wiley.com/doi/pdf/10.1111/j.1740-9713.2013.00636.x