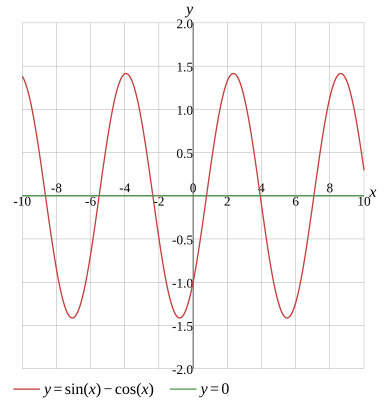
\sin(x)-\cos(x)=0
error msg
- Algebra
- Calculus
- Trigonometry
- Matrix
- Differential
- Integral
- Trigonometry
- Letters
Question
\sin\left(x\right)-\cos\left(x\right)=0
Solve the equation
x=\frac{\pi }{4}+k\pi ,k \in \mathbb{Z}
Alternative Form
x=45^{\circ}+180^{\circ} k,k \in \mathbb{Z}
Alternative Form
x\approx 0.785398+k\pi ,k \in \mathbb{Z}
Evaluate
\sin\left(x\right)-\cos\left(x\right)=0
Move the expression to the right side
-\cos\left(x\right)=0-\sin\left(x\right)
Subtract the terms
-\cos\left(x\right)=-\sin\left(x\right)
Divide both sides
\frac{-\cos\left(x\right)}{\sin\left(x\right)}=-1
Divide the terms
More Steps
Evaluate
\frac{-\cos\left(x\right)}{\sin\left(x\right)}
\text{Use }\frac{-a}{b}=\frac{a}{-b}=-\frac{a}{b}\text{ to rewrite the fraction}
-\frac{\cos\left(x\right)}{\sin\left(x\right)}
Rewrite the expression
-\sin^{-1}\left(x\right)\cos\left(x\right)
Rewrite the expression
-\cot\left(x\right)
-\cot\left(x\right)=-1
\text{Multiply both sides of the equation by }-1
-\cot\left(x\right)\left(-1\right)=-\left(-1\right)
Calculate
\cot\left(x\right)=-\left(-1\right)
Multiplying or dividing an even number of negative terms equals a positive
\cot\left(x\right)=1
Use the inverse trigonometric function
x=\operatorname{arccot}\left(1\right)
Calculate
x=\frac{\pi }{4}
Solution
x=\frac{\pi }{4}+k\pi ,k \in \mathbb{Z}
Alternative Form
x=45^{\circ}+180^{\circ} k,k \in \mathbb{Z}
Alternative Form
x\approx 0.785398+k\pi ,k \in \mathbb{Z}
Show Solutions
Graph