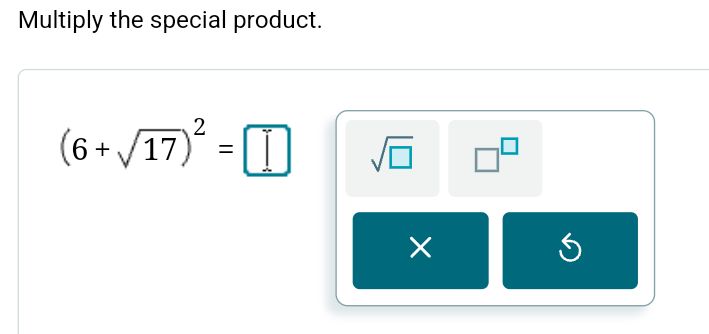
Multiply the special product. \[ (6+\sqrt{17})^{2}= \] \( \square \) \[ \sqrt{\square} \] \( \square \)
Upstudy AI Solution
Answer
Solution
Answered by UpStudy AI and reviewed by a Professional Tutor
 Explain
Explain  Simplify this solution
Simplify this solution Extra Insights
To multiply the special product \( (6+\sqrt{17})^{2} \), we can use the formula \( (a + b)^{2} = a^{2} + 2ab + b^{2} \). Here, \( a = 6 \) and \( b = \sqrt{17} \). Calculating: \[ (6+\sqrt{17})^{2} = 6^{2} + 2(6)(\sqrt{17}) + (\sqrt{17})^{2} \] \[ = 36 + 12\sqrt{17} + 17 \] \[ = 53 + 12\sqrt{17}. \] Thus, the first blank is \( 53 + 12\sqrt{17} \). Next, we need to evaluate \( \sqrt{\square} \): \[ \sqrt{53 + 12\sqrt{17}}. \] This doesn't simplify further without additional context or specific numbers, so we keep it as is. In conclusion: \((6+\sqrt{17})^{2} = 53 + 12\sqrt{17}\) and \( \sqrt{53 + 12\sqrt{17}} \).


