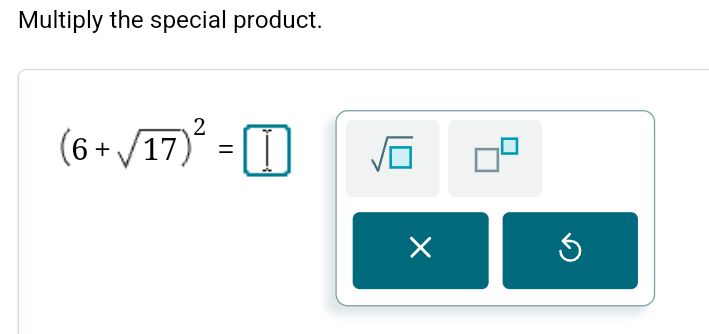
Multiply the special product. \[ (6+\sqrt{17})^{2}= \] \( \square \) \[ \sqrt{\square} \] \( \square \)

To multiply the special product \((6+\sqrt{17})^{2}\), we can use the formula for the square of a binomial: \[ (a + b)^2 = a^2 + 2ab + b^2 \] In this case, let \(a = 6\) and \(b = \sqrt{17}\). Now we can calculate each term: 1. Calculate \(a^2\): \[ a^2 = 6^2 = 36 \] 2. Calculate \(2ab\): \[ 2ab = 2 \cdot 6 \cdot \sqrt{17} = 12\sqrt{17} \] 3. Calculate \(b^2\): \[ b^2 = (\sqrt{17})^2 = 17 \] Now, we can combine these results: \[ (6+\sqrt{17})^{2} = a^2 + 2ab + b^2 = 36 + 12\sqrt{17} + 17 \] Combine the constant terms: \[ 36 + 17 = 53 \] Thus, we have: \[ (6+\sqrt{17})^{2} = 53 + 12\sqrt{17} \] Now, we can fill in the squares in the original format: \[ (6+\sqrt{17})^{2} = 53 + 12\sqrt{17} \] So, we can write: \[ \square = 53 \] \[ \sqrt{\square} = \sqrt{53} \] \[ \square = 12 \] Final answer: \[ (6+\sqrt{17})^{2} = 53 + 12\sqrt{17} \] \(\square = 53\) \(\sqrt{\square} = \sqrt{53}\) \(\square = 12\)