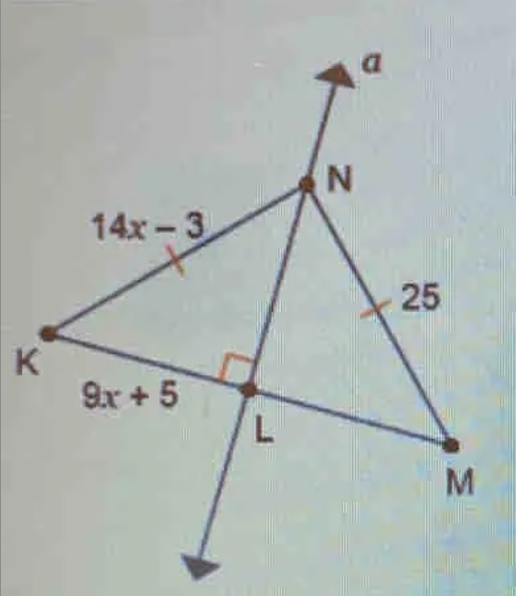
What is the length of segment LM?

To find the length of segment \(LM\), we need to first determine the value of \(x\) using the given lengths and then calculate \(LM\).
From the image, we see that \(\triangle KNL\) and \(\triangle NLM\) are right triangles with \(\angle KNL\) and \(\angle NLM\) both being right angles. 
Given:

• \(KN = 14x - 3\)
• \(KL = 9x + 5\)
• \(NM = 25\)
  Since \(KN= NM\), we can use \(25= 14x - 3\) to solve for\(x\)
  \(25= 14x - 3\) 
  \(28= 14x\) 
  \(x= 2\)
  \[KL = 9( 2) + 5 = 23\]
  \[LN^ 2 = 115( 2) ^ 2 - 174( 2) - 16 = 460 - 348 - 16 = 96\]
  Then:
  \[LM^ 2 = 625 - 96 = 529\]
  \[LM = \sqrt { 529} = 23\]
  Thus, the length of segment \(LM\) is \(\boxed{ 23} \).

Supplemental Knowledge

Understanding triangle properties and side relationships are fundamental concepts in geometry, especially with right triangles where understanding their Pythagorean Theorem becomes particularly helpful.It states that in a right triangle:
\[a^ 2 + b^ 2 = c^ 2\]
where \(c\) is the hypotenuse (the side opposite the right angle), and \(a\) and \(b\) are the other two sides.
In this problem, we are given two segments of a triangle with expressions involving \(x\). To find the length of segment LM, we need to solve for \(x\) first by setting up an equation based on given lengths.

Theory in Practice

Are You Building a Triangular Garden and Need Fencing Materials? By understanding geometric principles, understanding how to calculate precise lengths will enable you to purchase only what's necessary without waste and saving both time and money!

For those looking to deepen their understanding of geometric principles or needing assistance with complex mathematical problems, UpStudy offers an array of tools designed just for you.
Explore UpStudy’s live tutor question bank today – making your journey through understanding mathematics insightful and effective!
For precise calculations related to geometry problems like this one, check out UpStudy's Geometry Calculator! It's perfect for handling all your geometry-related queries efficiently!