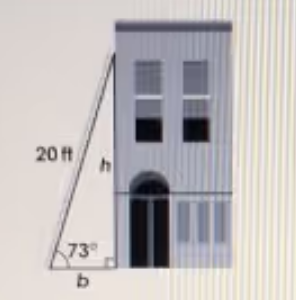
A 20-foot ladder is set up against a building so that the ladder makes an angle of 73° with the ground. The height, h, is the vertical distance from the top of the ladder to the base of the building. The base, b, is the horizontal distance from the bottom of the ladder to the base of the building. What is the approximate height-to-base ratio? \(sin73° \approx 0.9563\)\(cos73° \approx 0.2924\)\(tan73° \approx 3.2703\)3.27:1 0.31:1 3.42:1 0.96:1
Real Tutor Solution
Quick Answer
3.27:1
Step-by-step Solution
The height-to-base ratio can be determined using the tangent of the angle, which is the ratio of the opposite side (height, \(h\)) to the adjacent side (base, \(b\)).
Given:
\[\tan 73^ \circ \approx 3.2703\]
This means:
\[\frac { h} { b} \approx 3.2703\]
Therefore, the height-to-base ratio is approximately 3.27:1.
Supplemental Knowledge
In trigonometry, the tangent of an angle in a right triangle is the ratio of the length of the opposite side to the length of the adjacent side. This can be expressed as:
\[\tan ( \theta ) = \frac { \text { opposite} } { \text { adjacent} } \]
For your problem, we have:
- The ladder forms a right triangle with the building and the ground.
- The angle between the ladder and the ground is 73°.
- The height \(h\) is opposite to this angle.
- The base \(b\) is adjacent to this angle.
Concepts to Actions
Imagine setting up a ladder to clean windows on a tall building; understanding trigonometric ratios will enable you to ensure it is safely erected at an ideal angle and prevent accidents from happening. Understanding these ratios also has applications beyond cleaning windows - for instance architecture, engineering or even everyday tasks like ensuring ramp meets accessibility standards are some other areas in which trigonometric ratios prove valuable.
Curious about how trigonometric principles apply in real-world scenarios? UpStudy’s live tutor question bank offers detailed explanations on trigonometry and its practical applications. Dive into our AI-powered problem-solving services for personalized learning experiences!
For more insights into trigonometry or help with similar problems, explore UpStudy’s Trigonometric Functions Calculator or our AI-powered problem-solving services!
Enter your question here…