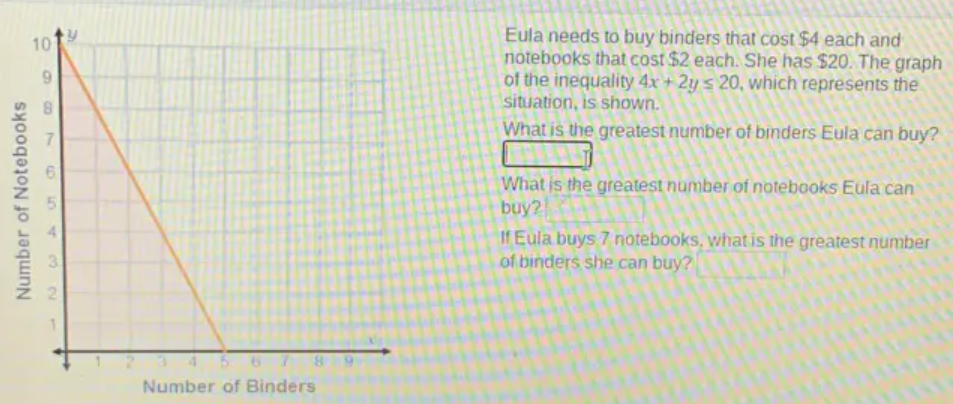
Eula needs to buy binders that cost $4 each and notebooks that cost $2 each. She has $20. The graph of the inequality 4x+2y≤ 20, which represents the situation, is shown. What is the greatest number of binders Eula can buy? \(\square \)What is the greatest number of notebooks Eula can buy? \(\square \)If Eula buys 7 notebooks, what is the greatest number of binders she can buy?\(\square \)

UpStudy Free Solution:

To solve these questions, we need to analyze the graph and the inequality \(4x + 2y \leq 20\), where \(x\) represents the number of binders and \(y\) represents the number of notebooks.

Greatest number of binders Eula can buy:
To find the greatest number of binders, we set \(y = 0\) (no notebooks) and solve for \(x\):
\[4x + 2( 0) \leq 20 \implies 4x \leq 20 \implies x \leq 5\]
So, the greatest number of binders Eula can buy is \(5\).
 

Greatest number of notebooks Eula can buy:
To find the greatest number of notebooks, we set \(x = 0\) (no binders) and solve for \(y\):
\[4( 0) + 2y \leq 20 \implies 2y \leq 20 \implies y \leq 10\]
So, the greatest number of notebooks Eula can buy is \(10\).
 

If Eula buys 7 notebooks, what is the greatest number of binders she can buy?
Substitute \(y = 7\) into the inequality and solve for \(x\):
\[4x + 2( 7) \leq 20 \implies 4x + 14 \leq 20 \implies 4x \leq 6 \implies x \leq 1.5\]
Since \(x\) must be an integer, the greatest number of binders Eula can buy is \(1\).

Supplemental Knowledge

Linear Inequalities:
Linear inequalities represent a range of possible solutions that satisfy the inequality condition. The inequality \(4x + 2y \leq 20\) represents the budget constraint where \(x\) is the number of binders and \(y\) is the number of notebooks.
Graph Interpretation:
The graph shows the feasible region where all points (x, y) satisfy the inequality. The boundary line \(4x + 2y = 20\) divides the plane into two regions, with the shaded area representing all possible combinations of binders and notebooks Eula can buy within her budget.

UpStudy offers precise, step-by-step solutions and explanations for homework problems across math, physics, chemistry and biology.