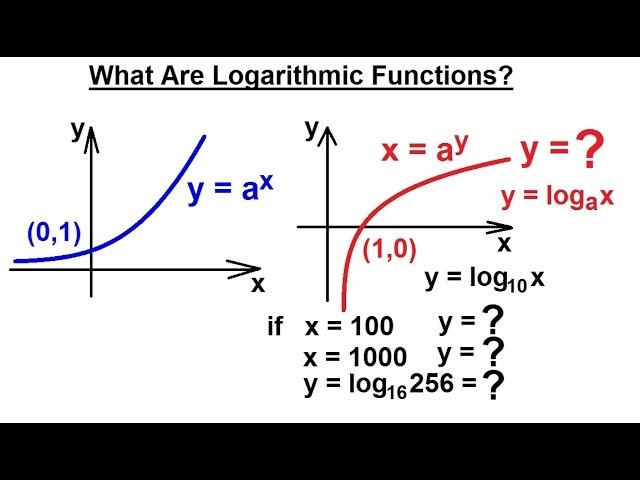
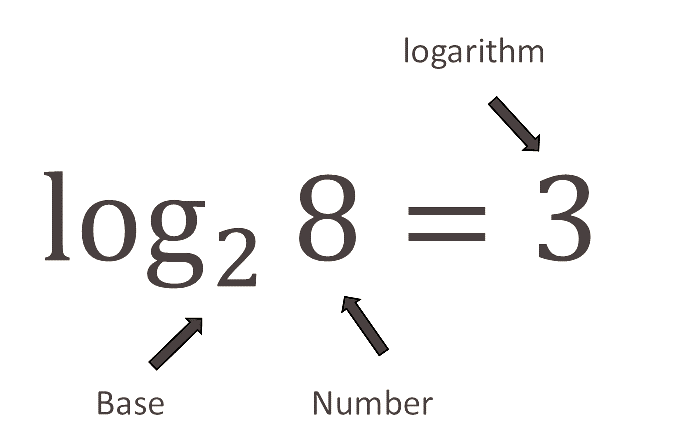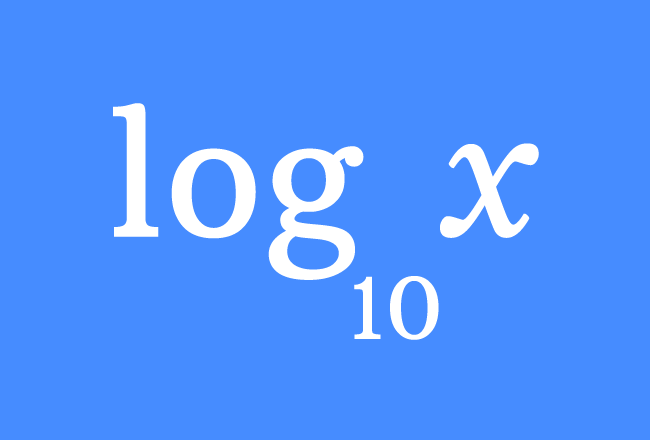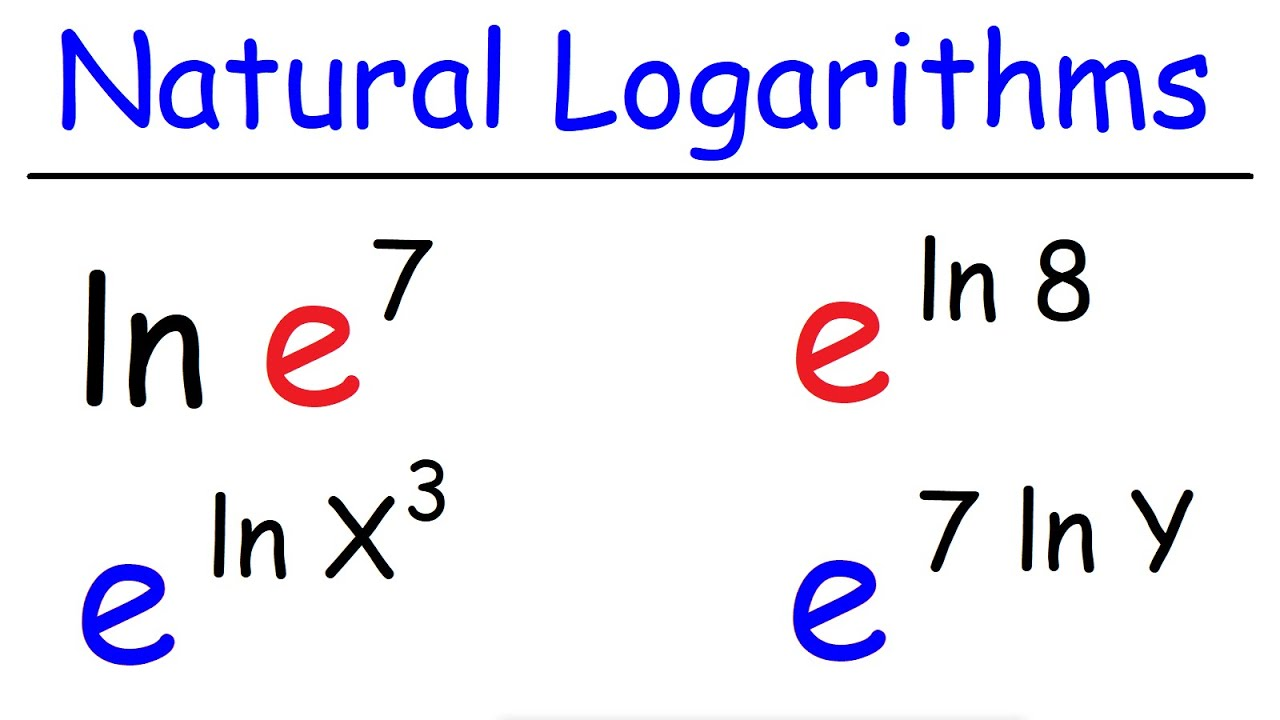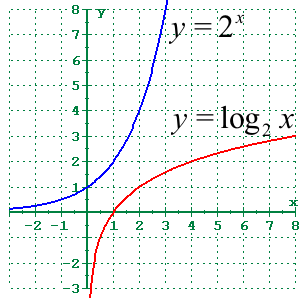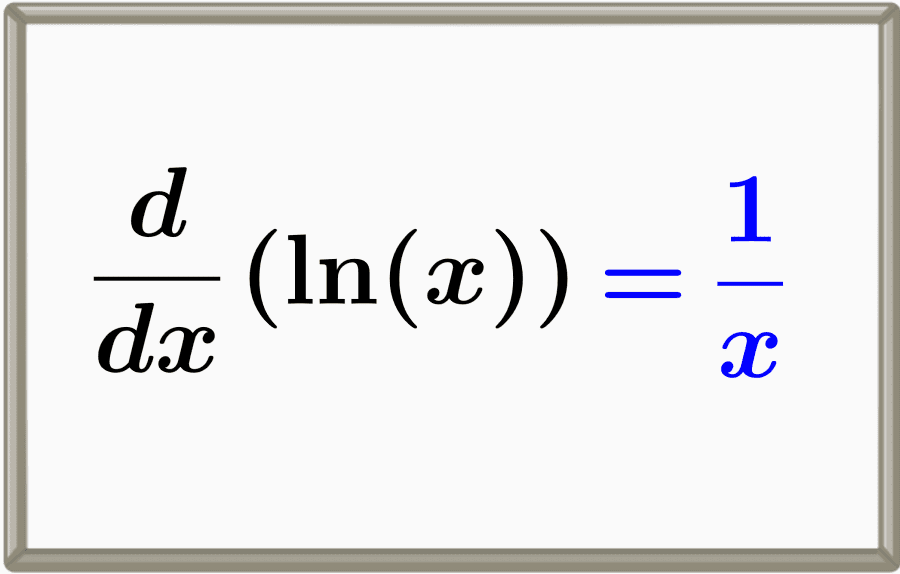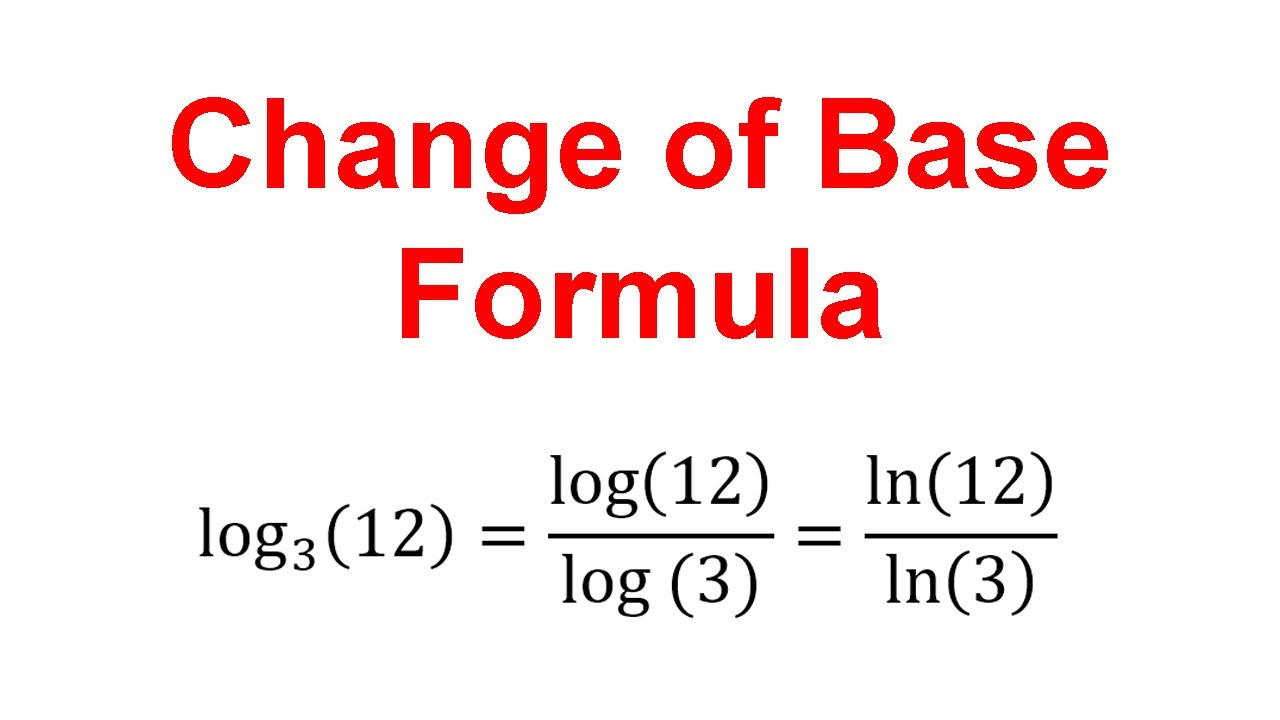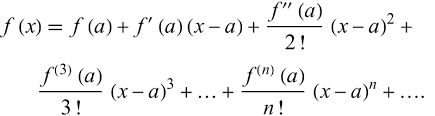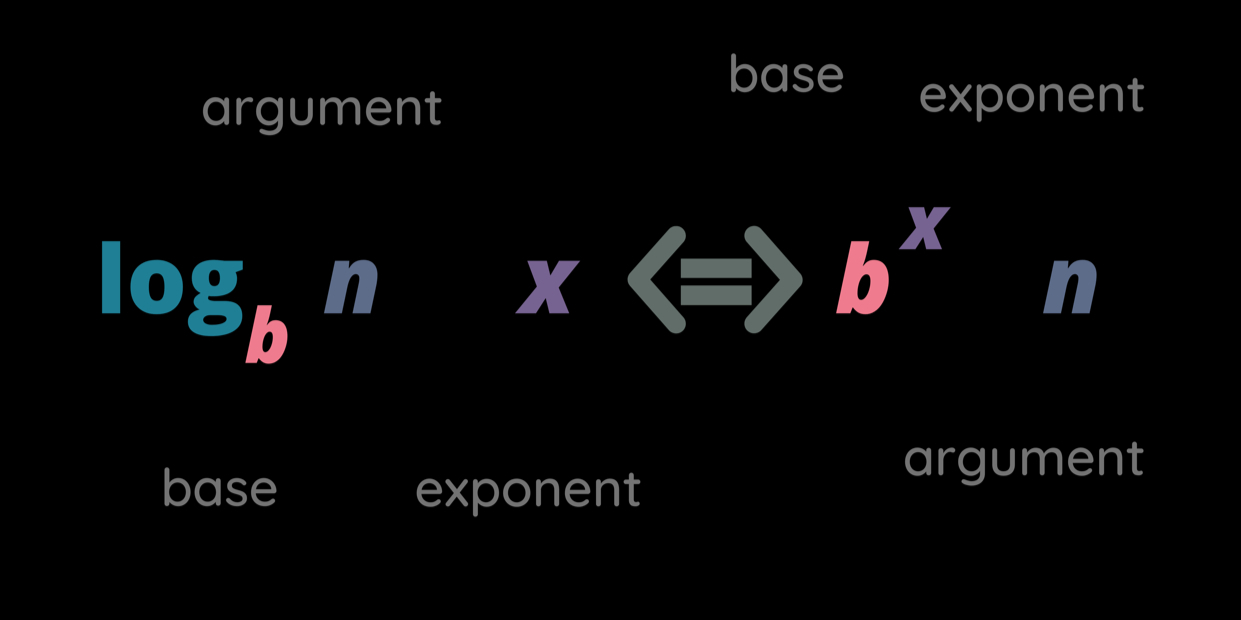¿Qué son las funciones logarítmicas?

Definición y Origen de las Funciones Logarítmicas

Definición Básica de Logaritmos

Los logaritmos son funciones que invierten operaciones exponenciales; es decir, invierten operaciones exponenciales y representan operaciones exponenciales negativas. La forma general de una función logarítmica se expresa como:  

\(\log_b(x) = y \iff b^y = x,\)

donde \(b > 0\), \(b \neq 1\), y \(x > 0\). En esta ecuación, \(b\) se refiere como la base del logaritmo. El valor \(y\) denota el exponente o potencia al que la base \(b\) se eleva para producir \(x\). Por ejemplo, dado que \(2^3 = 8\), se sigue que \(\log_2(8) = 3\).  

La función logarítmica efectivamente invierte el papel de la función exponencial, convirtiéndola en una herramienta matemática esencial. Los logaritmos pueden utilizarse para simplificar multiplicaciones y divisiones complejas en sumas y restas. La fórmula para cambiar la base de una función logarítmica también es útil al cambiar de una base a otra:  

\(\log_b(x) = \frac{\ln(x)}{\ln(b)},\)

donde \(\ln(x)\) es el logaritmo natural, con \(e\) (\(e \approx 2.718\)) como su base.  

Contexto Histórico de los Logaritmos

El concepto de logaritmos fue introducido a principios del siglo XVII por John Napier, un matemático escocés. Publicó tablas logarítmicas en 1614 para ayudar a simplificar tediosos cálculos matemáticos. El trabajo de Napier proporcionó a astrónomos, físicos e ingenieros una poderosa herramienta para realizar cálculos de manera más eficiente en una época en que la computación se realizaba manualmente.  

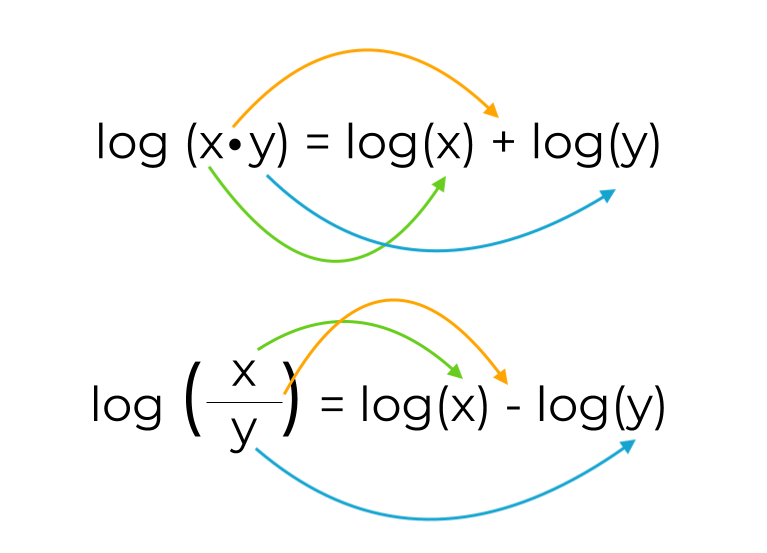
La importancia histórica de los logaritmos reside en su capacidad para transformar la multiplicación y división en sumas y restas, utilizando la propiedad:  

\(\log_b(x \times y) = \log_b(x) + \log_b(y).\)

Por ejemplo, calcular \(1,000 \times 50,000\) manual podría ser engorroso, pero las tablas logarítmicas simplificaron esto en una suma:  

\(\log_{10}(1,000) + \log_{10}(50,000).\)

Las funciones logarítmicas sentaron las bases para técnicas computacionales utilizadas en varios campos, como la navegación, astronomía e ingeniería. Antes de la llegada de calculadoras y computadoras, herramientas como la regla de cálculo se basaban en escalas logarítmicas para cálculos rápidos, avanzando significativamente el progreso científico e industrial durante los siglos XVIII y XIX.

Tipos de Funciones Logarítmicas

Logaritmo Común

El logaritmo común, denotado como \(\log(x)\), es un logaritmo con base 10. Por ejemplo:

\(\log_{10}(1000) = 3 \quad \text{porque} \quad 10^3 = 1000.\)

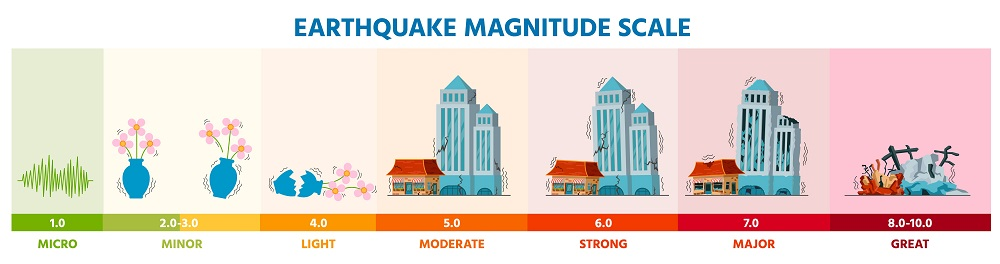
El logaritmo de base 10 es prevalente en muchas aplicaciones del mundo real, particularmente en campos científicos. Un ejemplo destacado es la escala de Richter, que mide la magnitud de los terremotos. En esta escala logarítmica, cada incremento de un número entero corresponde a un aumento de diez veces en la amplitud del terremoto:

\(\text{Magnitud} = \log_{10}\left(\frac{I}{I_0}\right),\)

donde \(I\) es la intensidad sísmica medida y \(I_0\) es un valor de referencia.

Otra aplicación de los logaritmos comunes aparece en química, específicamente en la escala de pH que mide la acidez de una solución:

\(\text{pH} = -\log_{10}[\text{H}^+],\)

donde \([\text{H}^+]\) representa la concentración de iones de hidrógeno.

Logaritmo Natural

El logaritmo natural, representado como \(\ln(x)\), utiliza la base \(e\) (\(e \approx 2.718\)), una constante fundamental en matemáticas. Por ejemplo:

\(\ln(e^2) = 2.\)

Los logaritmos naturales son ampliamente utilizados para modelar el crecimiento o la disminución continua en matemáticas, economía, biología y otras disciplinas. La conexión entre los logaritmos naturales y el crecimiento exponencial surge de ecuaciones como \(P(t) = P_0 e^{rt}\), que describen el crecimiento poblacional, la descomposición radiactiva o los cálculos de intereses. Resolver para tiempo \(t\) en estas ecuaciones a menudo requiere del logaritmo natural.

Por ejemplo, en intereses compuestos, donde un capital \(P_0\) crece exponencialmente con el tiempo, el tiempo requerido para duplicar la inversión se puede calcular utilizando \(\ln(2)\):

\(t = \frac{\ln(2)}{r},\)

Donde \(r\) es la tasa de crecimiento anual.

Logaritmos Especializados

Además de los logaritmos comunes y naturales, otras funciones logarítmicas se utilizan en áreas especializadas:

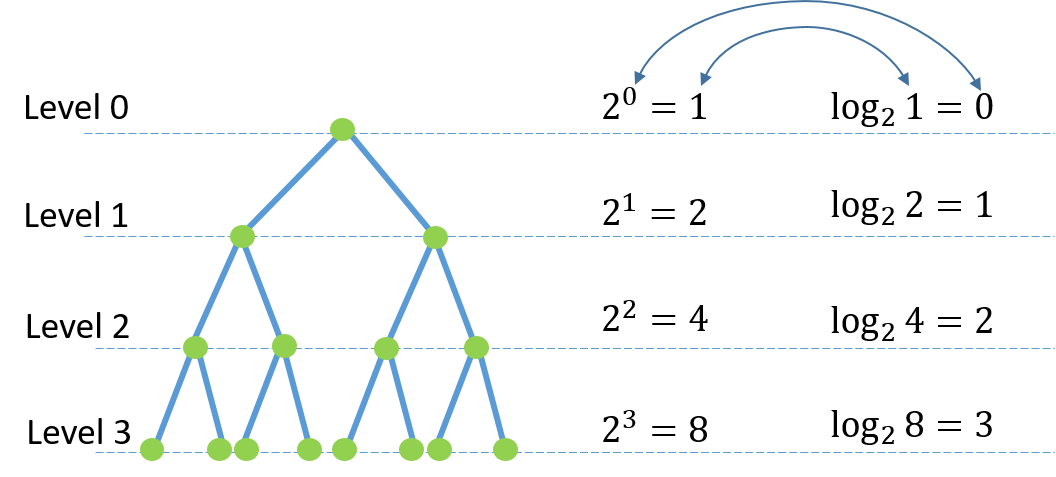
- Logaritmo Binario: \(\log_2(x)\), que usa base 2, es común en ciencias de la computación para medir tamaño de datos o eficiencia de algoritmos.

- Logaritmos Personalizados: Ciertas áreas aplican logaritmos adaptados a sus necesidades únicas. Por ejemplo, la escala de magnitud estelar en astronomía es logarítmica, capturando cómo el ojo humano percibe las diferencias de brillo.

En ciencia de datos, los logaritmos son cruciales para escalar y normalizar grandes conjuntos de datos. La "transformación logarítmica" puede reducir la asimetría, haciendo que los datos sean más interpretables en visualización y modelos estadísticos.

Propiedades y Reglas de las Funciones Logarítmicas

Propiedades Fundamentales

Las funciones logarítmicas obedecen a varias propiedades esenciales que simplifican las operaciones:

Regla del Producto:

\(\log_b(xy) = \log_b(x) + \log_b(y).\)

Por ejemplo: \(\log_2(8 \times 4) = \log_2(8) + \log_2(4) = 3 + 2 = 5.\)

Regla del Cociente:

\(\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y).\)

Por ejemplo: \(\log_3\left(\frac{81}{27}\right) = \log_3(81) - \log_3(27) = 4 - 3 = 1.\)

Regla del Poder:

\(\log_b(x^r) = r \cdot \log_b(x).\)

Por ejemplo: \(\log_2(8^2) = 2 \cdot \log_2(8) = 2 \cdot 3 = 6.\)

Estas propiedades se usan ampliamente para simplificar cálculos tanto en matemáticas teóricas como en aplicaciones prácticas.

Relación entre Logaritmos y Exponenciales

Las funciones logarítmicas y las funciones exponenciales son operaciones inversas. Por ejemplo:

\(b^{\log_b(x)} = x \quad \text{y} \quad \log_b(b^x) = x.\)

Esta relación forma la base de su uso en la resolución de ecuaciones exponenciales. Por ejemplo, dado \(10^x = 500\), resolvemos para \(x\) usando:

\(x = \log_{10}(500).\)

Este ejemplo ilustra cómo los logaritmos son herramientas indispensables en varios dominios.

Conceptos Erróneos sobre Logaritmos

Es esencial notar las limitaciones o conceptos erróneos asociados con los logaritmos. Por ejemplo:

\(\log_b(x + y) \neq \log_b(x) + \log_b(y),\)

y

\(\log_b(x - y) \neq \log_b(x) - \log_b(y).\)

La aplicación errónea de estas propiedades puede conducir a errores en la resolución de problemas matemáticos. Por ejemplo, \(\log_{10}(2 + 3) \neq \log_{10}(2) + \log_{10}(3)\). El uso correcto es vital para asegurar resultados precisos.

Características Gráficas y Geométricas de las Funciones Logarítmicas

Características del Gráfico

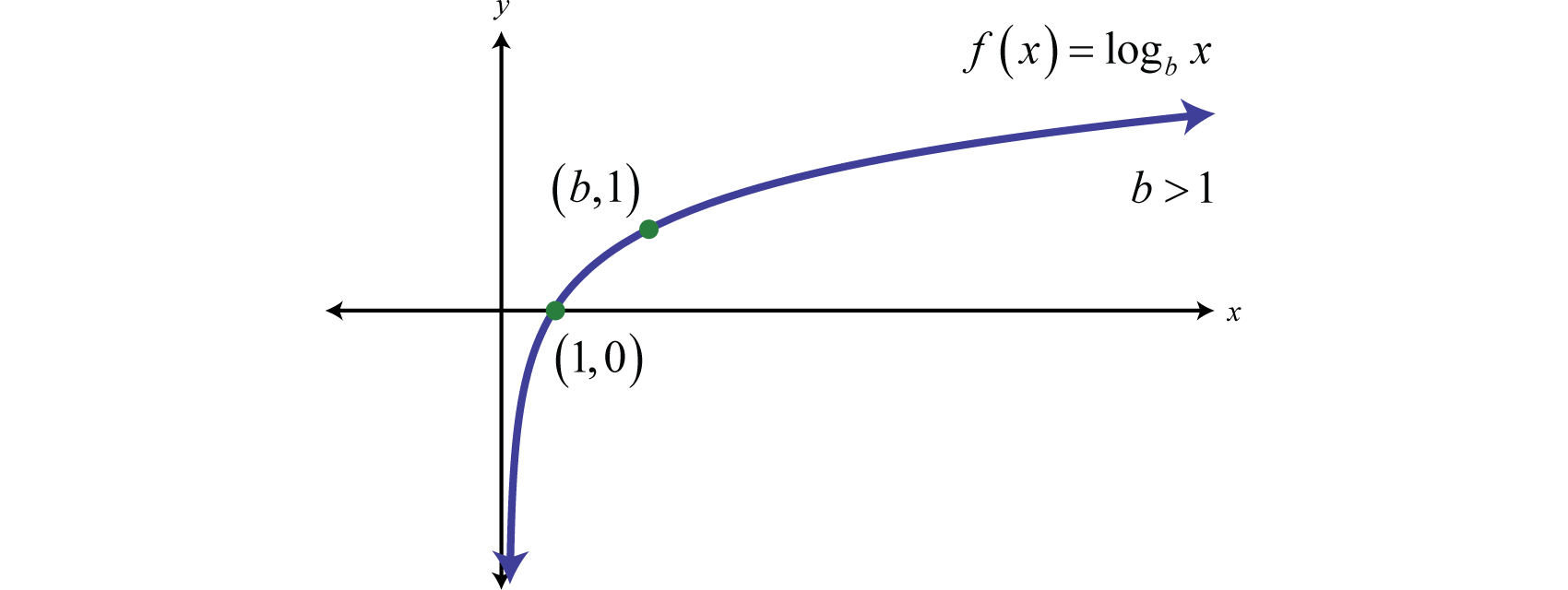
El gráfico de una función logarítmica ofrece importantes ideas sobre su comportamiento. Para una función logarítmica de la forma \(\log_b(x)\), se cumplen las siguientes características:   

El dominio de una función logarítmica está limitado a números reales positivos, donde \(x > 0\). Esta restricción surge porque los logaritmos están indefinidos para valores no positivos de \(x\). Por ejemplo, \(\log_b(-1)\) no existe en el sistema de números reales.

Rango

El rango de una función logarítmica consiste en todos los números reales, \((-\infty, +\infty)\). Esto significa que una función logarítmica puede dar cualquier valor real como resultado. Por ejemplo, \(\log_2(1/2) = -1\), y \(\log_2(8) = 3\).   

Asíntota Vertical

El gráfico de \(\log_b(x)\) tiene una asíntota vertical en \(x = 0\). A medida que \(x\) se aproxima a cero desde la derecha, la función tiende hacia el infinito negativo.

Intersección

Para \(\log_b(x)\), la intersección en el eje \(x\) ocurre en \(x = 1\), porque \(\log_b(1) = 0\).   

Por ejemplo, el gráfico de \(\log_{10}(x)\) comienza cerca del infinito negativo cuando \(x\) se aproxima a 0 desde la derecha, pasa por (1, 0) y crece constantemente mientras se aplana para \(x\) mayores. 

Simetría con Funciones Exponenciales   

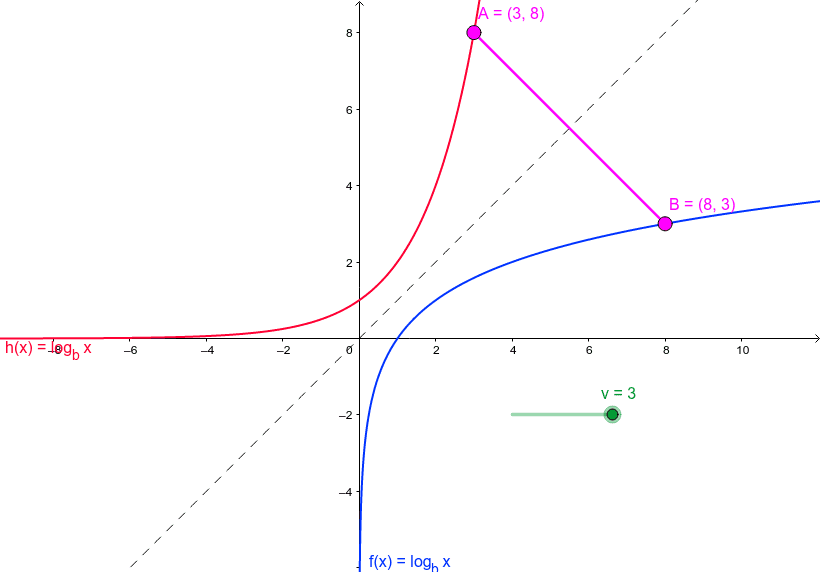
Las funciones logarítmicas y exponenciales son reflejos una de la otra a través de la línea \(y = x\). La esencia de esta simetría radica en su relación inversa. Matemáticamente:   

\(f(x) = b^x \quad \text{y} \quad g(x) = \log_b(x),\)

resultan en \(f(g(x)) = x\) y \(g(f(x)) = x\). Esta simetría es visualmente significativa, ya que la curva exponencial aumenta abruptamente mientras que la curva logarítmica crece gradualmente.   

Esta relación inversa es fundamental para numerosas aplicaciones, incluidas ecuaciones que implican crecimiento compuesto o decaimiento exponencial. Por ejemplo, resolver \(2^x = 32\) requiere encontrar \(x = \log_2(32) = 5\), invirtiendo efectivamente el proceso exponencial.   

Tendencias en Gráficas Logarítmicas   

El gráfico logarítmico crece indefinidamente pero a una tasa decreciente. Esta tasa de crecimiento gradual hace que los logaritmos sean adecuados para aplicaciones donde las diferencias relativas importan más que los valores absolutos. Ejemplos incluyen los niveles de decibelios en audio y la escala de pH en química, donde la escala logarítmica simplifica la representación de amplios rangos dinámicos.   

Aplicaciones de las Funciones Logarítmicas  

Aplicaciones Científicas en el Mundo Real  

Las funciones logarítmicas encuentran un uso extenso en ciencia e ingeniería debido a su capacidad para comprimir grandes rangos de valores en escalas manejables.  

Magnitud de Terremotos (Escala de Richter)

La magnitud \(M\) de un terremoto se calcula utilizando la escala logarítmica de Richter:

\(M = \log_{10}\left(\frac{I}{I_0}\right),\)

donde \(I\) representa la intensidad del terremoto, y \(I_0\) es una intensidad de referencia. Por ejemplo, un terremoto con \(I = 10,000 \cdot I_0\) tiene una magnitud de \(\log_{10}(10,000) = 4\).  

Química (Escala de pH)

Para indicar la acidez o alcalinidad de una solución, la escala de pH utiliza una escala logarítmica:

\(\text{pH} = -\log_{10}[\text{H}^+],\)

donde \([\text{H}^+]\) es la concentración molar de iones de hidrógeno. Por ejemplo, una solución con \([\text{H}^+] = 10^{-3}\) mol/L tiene un pH de \(3\). La naturaleza logarítmica de la escala de pH comprime el amplio rango de concentraciones de iones de hidrógeno en una escala limitada de 0 a 14.  

Desintegración Radiactiva

Las funciones logarítmicas modelan el tiempo que tarda en desintegrarse una sustancia radiactiva. La ecuación que describe la desintegración está relacionada con el logaritmo natural:  

\(N(t) = N_0 e^{-kt}, \quad \ln\left(\frac{N_0}{N(t)}\right) = kt,\)

donde \(N(t)\) es la cantidad que queda en el tiempo \(t\), \(N_0\) es la cantidad inicial, y \(k\) es la constante de desintegración.  

Logaritmos en Ciencia de Datos y Tecnología  

Transformación y Compresión de Datos

Las transformaciones logarítmicas pueden ayudar a los practicantes de ciencia de datos a abordar conjuntos de datos desbalanceados al normalizar valores atípicos, controlar la varianza y reducir valores extremos, lo cual ha demostrado ser particularmente útil en estudios de distribución de riqueza donde el rango de ingresos varía de cientos a miles de millones y requiere una transformación logarítmica para presentar los datos gráficamente de forma más clara.

Eficiencia de Algoritmos

El logaritmo en base 2, \(\log_2(x)\), juega un papel vital en el análisis de complejidad computacional. Algoritmos de ordenamiento, como QuickSort y MergeSort, operan con eficiencia logarítmica, denotada como \(O(n \log_2(n))\).  

Algoritmos de Búsqueda y Árboles Binarios

La búsqueda binaria, que divide los datos en mitades, se ejecuta en \(O(\log_2(n))\) de complejidad temporal. En informática, estructuras logarítmicas como los árboles de búsqueda binarios aseguran un almacenamiento y recuperación eficientes de datos.  

Percepción Humana y Psicología  

El sistema sensorial humano a menudo opera en una escala logarítmica en lugar de una lineal:  

Intensidad del Sonido (Escala de Decibelios)

La intensidad relativa del sonido se mide en decibelios (dB), que utiliza una escala logarítmica:  

\(\text{dB} = 10 \cdot \log_{10}\left(\frac{I}{I_0}\right),\)

donde \(I\) denota la intensidad del sonido, y \(I_0\) es una intensidad de referencia. Por ejemplo, un incremento de 100 veces en la intensidad del sonido corresponde a \(10 \cdot \log_{10}(100) = 20 \, \text{dB}\).  

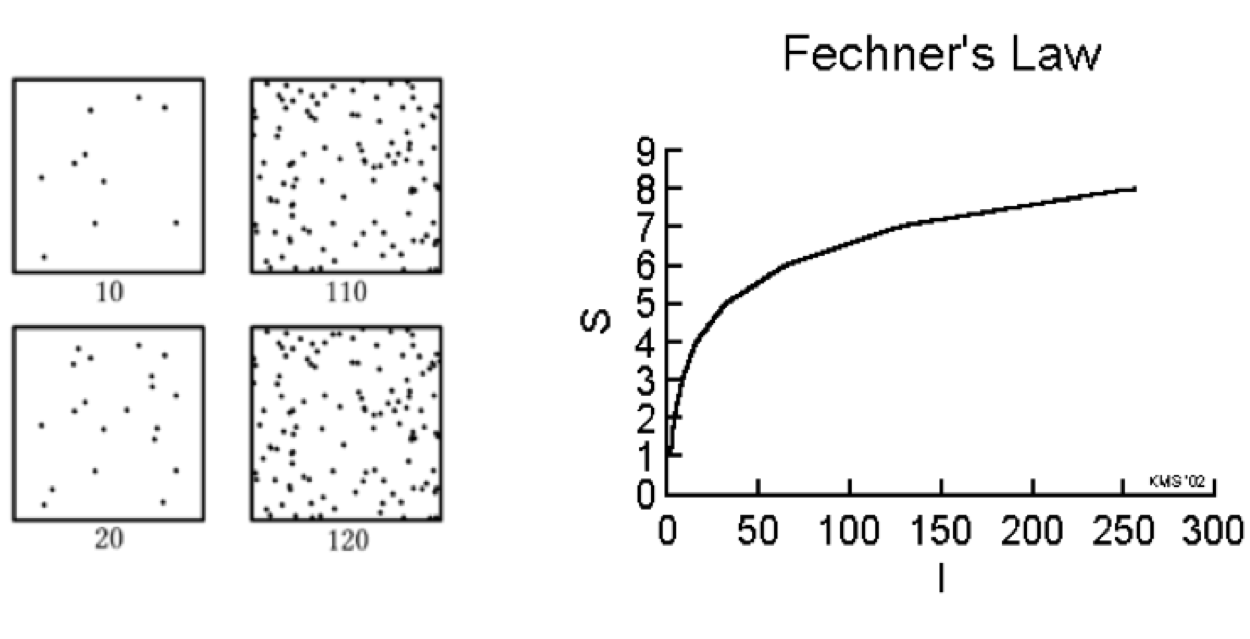
Ley de Fechner en Psicología

La Ley de Fechner postula que la intensidad percibida de un estímulo crece logarítmicamente con su magnitud real. Por ejemplo, duplicar el brillo de una fuente de luz no resulta en una duplicación de su intensidad percibida.  

Conexiones Interdisciplinarias de las Funciones Logarítmicas  

Relación con el Cálculo  

Las funciones logarítmicas están estrechamente vinculadas al cálculo, particularmente en la diferenciación e integración:  

Derivada del Logaritmo Natural

\(\frac{d}{dx} \ln(x) = \frac{1}{x}, \quad \frac{d}{dx} \log_b(x) = \frac{1}{x \ln(b)}.\)

Por ejemplo, la derivada de \(\ln(5x)\) es:  

\(\frac{d}{dx} \ln(5x) = \frac{1}{5x} \cdot 5 = \frac{1}{x}.\)

Integración

La integral del logaritmo natural está dada por:  

\(\int \ln(x) \, dx = x \ln(x) - x + C.\)

Este resultado a menudo aparece en problemas que involucran funciones logarítmicas en contextos de crecimiento o decrecimiento.  

Uso en Análisis Complejo  

En el análisis complejo, los logaritmos se extienden más allá de la línea real hacia el plano complejo. Una relación clave se expresa como:  

\(\ln(z) = \ln|z| + i\arg(z),\)

donde \(z\) es un número complejo, \(\ln|z|\) es el logaritmo natural del módulo, y \(\arg(z)\) es el argumento de \(z\).  

Los logaritmos en el plano complejo exhiben periodicidad, con múltiples "ramos" debido a la naturaleza repetitiva del argumento \(\arg(z)\). Esto hace que los logaritmos sean esenciales en campos como el procesamiento de señales y la mecánica de ondas.  

Técnicas para Calcular Valores Logarítmicos  

Métodos de Cálculo Preciso  

Calcular valores logarítmicos a menudo se basa en técnicas de estimación o soluciones exactas usando calculadoras o tablas logarítmicas. Para ciertos valores de \(x\), los logaritmos se pueden calcular directamente:  

Para Potencias Exactas de la Base

Los logaritmos son sencillos de calcular cuando \(x\) es una potencia exacta de la base. Por ejemplo:  

\(\log_2(32) = 5 \quad \text{porque} \quad 2^5 = 32.\)

Logaritmos Naturales de \(e^n\)

\(\ln(e^4) = 4 \quad \text{y} \quad \ln(1) = 0.\)

Estos cálculos directos son fundamentales en matemáticas y aparecen frecuentemente en varias aplicaciones.  

Fórmula de Cambio de Base

Cuando la base del logaritmo no es conveniente, se puede usar la fórmula de cambio de base:  

\(\log_b(x) = \frac{\log_k(x)}{\log_k(b)},\)

donde \(k\) es cualquier número positivo, comúnmente \(10\) o \(e\).  

Por ejemplo, para calcular \(\log_2(50)\):  

\(\log_2(50) = \frac{\ln(50)}{\ln(2)}.\)

Aquí, usando una calculadora:  

\(\ln(50) \approx 3.912 \quad \text{y} \quad \ln(2) \approx 0.693,\)

Entonces:  

\(\log_2(50) = \frac{3.912}{0.693} \approx 5.64.\)

La fórmula de cambio de base es particularmente útil en campos como la informática, donde los logaritmos binarios (\(\log_2\)) son frecuentemente necesarios pero no están soportados de manera nativa por las calculadoras estándar.  

Cálculo Mental y Técnicas de Aproximación  

Para fines prácticos, particularmente cuando los valores exactos no son necesarios, se pueden aplicar técnicas aproximadas para calcular valores logarítmicos:  

Logaritmo de Números Cerca de las Potencias de la Base  

Los números cercanos a la potencia de la base se pueden aproximar reconociendo su desviación. Por ejemplo:  

\(\log_{10}(120) \approx \log_{10}(100) + \log_{10}(1.2).\)

Dado que \(\log_{10}(100) = 2\) y \(\log_{10}(1.2) \approx 0.08\):  

\(\log_{10}(120) \approx 2.08.\)

Uso de Puntos de Referencia Aproximados

Para la base 2, los puntos de referencia incluyen:  

\(\log_2(1) = 0, \quad \log_2(2) = 1, \quad \log_2(4) = 2, \quad \log_2(8) = 3.\)

Para aproximar \(\log_2(20)\):  

Reconocer \(16 < 20 < 32\), así \(4 < \log_2(20) < 5\). Usando interpolación lineal se obtiene una estimación más cercana de aproximadamente \(4.32\).  

Expansión en Serie de Taylor

Para valores cercanos a 1, el logaritmo natural se puede aproximar usando:  

\(\ln(1+x) = x - \frac{x^2}{2} + \frac{x^3}{3} - \cdots.\)

Por ejemplo, para \(x = 0.1\):  

\(\ln(1.1) \approx 0.1 - \frac{0.1^2}{2} + \frac{0.1^3}{3} = 0.1 - 0.005 + 0.000333 = 0.095333.\)

Estas técnicas permiten cálculos y estimaciones rápidas, especialmente en campos donde los valores logarítmicos se calculan frecuentemente sin necesidad de alta precisión.  

Direcciones Futuras e Impacto de las Funciones Logarítmicas  

Seguridad de Datos y Cifrado  

Las funciones logarítmicas son críticas para los métodos de cifrado modernos y la seguridad de datos. Por ejemplo, el protocolo de intercambio de claves Diffie-Hellman se basa en la dificultad de resolver logaritmos discretos en campos finitos para transferencias de datos seguras. El cálculo subyacente involucra resolver ecuaciones de la forma:  

\(g^x \mod p,\)

donde la operación inversa (calcular \(x\)) es inviable sin recursos computacionales significativos.  

A medida que crece el poder computacional, los investigadores están explorando logaritmos y sus extensiones en la criptografía cuántica, asegurando una comunicación segura en la era de la computación cuántica.  

Uso en Ciencia del Clima y Modelado  

Las funciones logarítmicas desempeñan un papel vital en la comprensión y predicción de cambios en el clima de la Tierra. Por ejemplo:  

Concentración de CO\(_2\) y Forzamiento Radiativo

La relación entre las concentraciones de CO\(_2\) atmosférico y el forzamiento radiativo de la Tierra sigue un modelo logarítmico:  

\(\Delta F = \alpha \cdot \ln\left(\frac{C}{C_0}\right),\)

donde \(C\) es el nivel actual de CO\(_2\), \(C_0\) es el nivel preindustrial, y \(\alpha\) es una constante.  

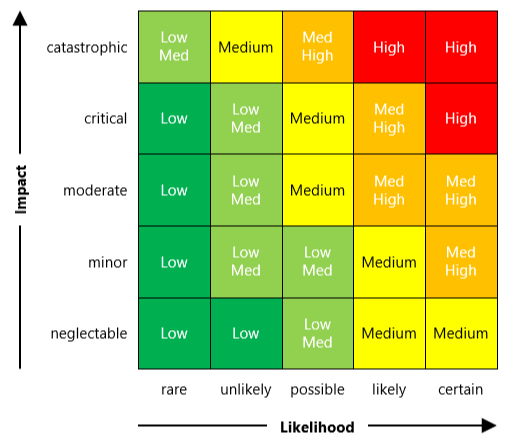
Evaluaciones de Riesgo y Escalas Logarítmicas

Las funciones logarítmicas ayudan a los científicos a visualizar riesgos y umbrales para puntos de inflexión, ya que pequeños cambios exponenciales en gases de efecto invernadero pueden tener efectos logarítmicos en el aumento de temperatura.  

Extendiendo Logaritmos a Campos Emergentes  

Inteligencia Artificial y Escalado de Eficiencia

Las funciones logarítmicas se utilizan a menudo para modelar la disminución de los rendimientos en el desempeño de redes neuronales a medida que aumenta el tamaño del modelo. Por ejemplo, duplicar el número de parámetros en un modelo de aprendizaje profundo mejora la precisión de manera logarítmica, destacando compensaciones en la asignación de recursos.  

Ciencia de la Información Cuántica

En mecánica cuántica, el logaritmo de amplitudes de probabilidad se aplica en mediciones de entropía, como la entropía de Von Neumann:  

\(S = -\text{Tr}(\rho \ln(\rho)),\)

Donde \(\rho\) es la matriz de densidad de un estado cuántico. Esta aplicación demuestra la profunda conexión entre logaritmos y teoría de la información.  

Modelado Económico y Financiero

Las funciones logarítmicas son la base de modelos económicos como la teoría de la utilidad, que mide la satisfacción humana logarítmicamente en relación con el consumo de recursos. Este enfoque apoya iniciativas de crecimiento sostenible al enfatizar ganancias relativas en lugar de absolutas.

Conclusión  

Las funciones logarítmicas ocupan un lugar invaluable en matemáticas y sus aplicaciones, sirviendo a una multitud de disciplinas desde ciencias como la biología hasta la ingeniería y la tecnología. Sus propiedades - que van desde convertir la multiplicación en suma, simplificar escalas y modelar el crecimiento - hacen de las funciones logarítmicas herramientas indispensables en aplicaciones científicas, de ingeniería y tecnológicas. Desde explicar fenómenos naturales como la descomposición exponencial hasta impulsar avances en investigación sobre encriptación e inteligencia artificial, las funciones logarítmicas revelan tanto abstracción como aplicación en el mundo real, mostrando su elegancia matemática al actuar como puentes entre varios campos mientras abren nuevas avenidas que permiten innovaciones que moldean tanto nuestra comprensión de la historia del mundo como su desarrollo futuro.

Referencia:

https://www.britannica.com/science/Richter-scale

https://www.bigocheatsheet.com/

https://rss.onlinelibrary.wiley.com/doi/pdf/10.1111/j.1740-9713.2013.00636.x