How to Factorize Cubic Equation?

What is a Cubic Equation?

Definition and Standard Form

Cubic equations belong to the category of polynomials—expressions that involve powers of an unknown variable. As the name suggests, a cubic equation is a polynomial of degree three, indicating that the highest power of the unknown variable (x ) is three. Such an equation is expressed in its standard form as:

\(ax^{3} + bx^{2} + cx + d = 0\),

In this context, a, b, c, and d are constants, and \(a \ne 0\) because without the cubic term, the equation would cease to be a cubic equation. The degree of an equation allows it to contain up to three roots - real or complex. These roots serve as the crux of its solution by representing where polynomials intersect the x-axis graphs.

Real Roots and Complex Roots

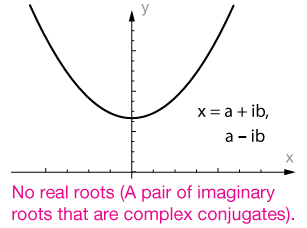
According to the Fundamental Theorem of Algebra, every cubic equation is guaranteed to have at least one real root. However, the distribution of the remaining roots depends on the coefficients of the equation. After finding one real root, the cubic can often be reduced to a quadratic, whose roots could be either real or a pair of complex conjugates. If all three roots of a cubic equation are real, its graph will cross the x-axis at three distinct points; otherwise, it intersects once with an "oval shape" created by imaginary roots that exhibit "twistiness."

Locating either real or complex roots often depends upon using effective factorization techniques that divide a cubic equation into simpler components.

Importance of Factorization

Factorizing cubic equations involves breaking up polynomials into their component terms - linear and quadratic factors combined - so as to simplify finding roots of each polynomial. Once factorized, each root corresponds with one factor from this set; once factorized again each root corresponds with specific root(s). Furthermore factorization helps understand intercepts and turning points of graph corresponding to cubic equation.

An engineer analyzing equilibrium forces in a structure might require factorizing a cubic equation representing load distribution to calculate its roots; factorization simplifies these calculations and permits more precise stress point determination. Furthermore, business profit/cost relationships frequently exhibit nonlinear behavior, providing cubic factorization with valuable insight into key points like breakeven points or optimal pricing decisions.

Factorization offers more than practical applications; it provides deeper mathematical insight. Factorization reveals symmetries, relationships between coefficients and roots, complex system behavior analysis. Mastery of cubic factorization connects theoretical understanding with real world problem-solving - essential skills across mathematics, science and beyond!

Methods for Factorizing Cubic Equations

Factorizing cubic equations involves breaking a cubic polynomial down into simpler components - usually linear and quadratic factors - using various strategies. This technique can uncover roots of an equation, simplify complex expressions, analyze its behavior, and uncover hidden roots of polynomials. We discuss some strategies below, including special cases grouping linear factors through division and advanced techniques; each has its own applicability depending on the structure of an equation.

Special Cases of Cubic Equations

Recognizing certain cubic equations has the advantage of making factorization easy; being aware of such patterns will save both time and energy in factorization efforts.

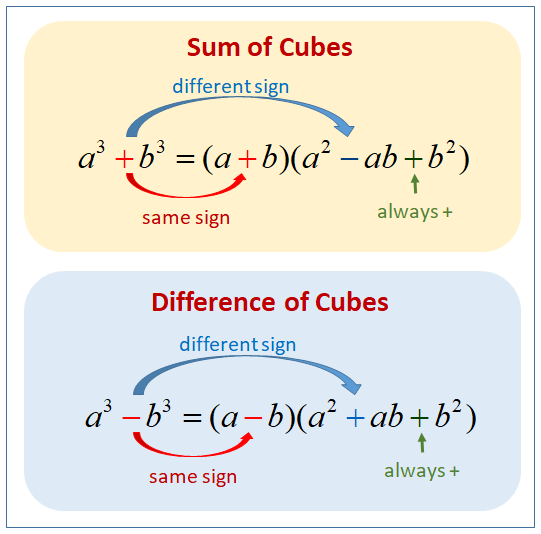
Sum and Difference of Cubes

Equations that are sums or differences of perfect cubes can be factorized using the following algebraic identities:

\(a^{3} +b^{3} =(a+b)(a^{2}−ab+b^{2})\)

\(a^{3}−b^{3}=(a−b)(a^{2}+ab+b^{2})\)

These formulas apply directly when the cubic terms can be expressed as perfect cubes. The signs in the factors can be remembered using the mnemonic "SOAP":

S ame sign as the original in the first factor,

O pposite sign in the middle term of the quadratic factor,

A lways

P ositive in the last term.

Example 1: Sum of Cubes

Factorize x^{3}+27:

x^{3}+27=x^{3}+3^{3}=(x+3)(x^{2}−3x+9)

Example 2: Difference of Cubes

Factorize x^{3}−8:

x^{3}−8=x^{3}−2^{3}=(x−2)(x^{2}+2x+4)

These forms are particularly common in both algebraic computations and real-world applications.

Pure Cubic Forms Without Linear Terms

Sometimes, cubic equations lack certain intermediate terms, appearing in the simplified form \(ax^{3}+d=0\). These can be factorized by directly extracting common factors.

Example: Factorize \(x^{3}−9x=0\):

Extract the common factor x:

\(x(x^{2}−9)=0\)

Factorize the resulting quadratic:

x(x−3)(x+3)=0

Graphical Insight:

For such equations, the cubic graph intersects the x-axis at x=0 and the other roots (e.g., −3 and 3 in the example above). Factorization reveals these points directly and simplifies further calculations.

H3: Factorization by Grouping

When a cubic equation doesn't fit standard identities or forms, the grouping method can often be applied. Grouping rearranges and pairs terms in the cubic equation, allowing partial factorization step-by-step.

Steps for Factorization by Grouping:

Split the terms into two groups: Divide the equation into two pairs of terms that suggest a common factor.

Factor each group individually: Extract the greatest common factor for each group.

Combine common factors: If both groups share a common binomial factor, factor it out.

Example: Factorize \(2x^{3}−3x^{2}−2x+3\):

Group terms:

\((2x^{3}−3x^{2})+(−2x+3)\)

2. Factor out common factors from each group:

\(x^{2}(2x−3)−1(2x−3)\)

3. Combine the common binomial factor:

\((2x−3)(x^{2}−1)\)

4. Further, factorize if possible:

(2x−3)(x−1)(x+1)

This method is effective for equations where terms can naturally pair to reveal a common binomial. You can try more exercise on question bank about equations.

Using Linear Factors to Find Quadratic Factors

Finding one real root and using it to deduce other factors for general cubic equations that don't follow particular patterns or grouping is essential when solving general cubic equations that do not comply with specific patterns, grouping, or grouping; this method utilizes both remainder theorem and polynomial division.

Step 1: Use the Remainder Theorem

According to the Remainder Theorem, if P(a)=0, then (x−a) serves as a factor of P(x). Start by guessing potential roots by testing logical values like ±1,±2,±3, etc.

Step 2: Perform Polynomial Division

Once a root has been identified, divide the cubic polynomial by its linear factor (x-a). After doing this, polynomial long division or synthetic division is used to locate and extract any remaining quadratic factors.

Example: Factorize \(x^{3}−6x^{2}+11x−6\):

Guess potential roots (x=1, x=2, etc.) and test:

\(P(1)=1^{3}−6(1^{2})+11(1)−6=0\) (Root found at x=1).

Divide \(x^{3}−6x^{2}+11x−6\) by (x−1):

\(\frac{x^{3}−6x^{2}+11x−6}{x-1} =x^{2}−5x+6\)

Factorize the quadratic:

\(x^{2}−5x+6=(x−2)(x−3)\)

Combine all factors:

\(x^{3}−6x^{2}+11x−6=(x−1)(x−2)(x−3)\)

This method is particularly useful for equations with integer roots and ensures the entire factorization process is systematic.

Advanced Methods for Factorizing Cubic Equations

When no obvious root is available, or the equation involves difficult coefficients, advanced techniques come into play:

Using Vieta's Formulas

The solutions of the cubic equation \(ax^{3}+bx^{2}+cx+d=0\) adhere to the following relationships:

The sum of roots: \(r_{1} +r_{2} +r_{3} =−b/a\),

The sum of product pairs: \(r_{1}​r_{2}​+r_{2}​r_{3}​+r_{1}​r_{3}​=c/a\),

The product of roots: \(r_{1}r_{2}r_{3}​=−d/a\).

By combining this knowledge, specific patterns in the roots can sometimes be identified, leading to partial factorization.

Numerical Approximation

If integer roots are not evident, numerical methods can estimate one root. Techniques like Newton's Method or graph inspection provide rapid approximations, which can then be used for polynomial division to extract other factors.

Complex Roots and Completing the Factorization

If an equation involves complex roots, factorization may lead to quadratic terms with no real factors. For example:

\(x^{3}+4x=0⟹x(x^{2}+4)=0\)

Here, \(x^{2}+4=0\) yields complex roots x=±2i, so the full factorization includes both real and complex factors:

x(x−2i)(x+2i)

This step may become necessary when cubic equations govern phenomena involving oscillations, electrical circuits, or wave functions.

Master these methods--special case patterns, grouping, and division, as well as advanced techniques--for effectively handling cubic equations of different levels of difficulty. Every technique adds flexibility so that you can address nearly every cubic polynomial that comes your way.

Numerical Methods for Difficult Cubics

When cubic equations contain roots which are difficult to determine manually, numerical solutions may provide effective approximate solutions. When faced with such obstacles, numerical methods offer effective approximate solutions as an approximation tool.

Newton's Method

Newton's Method is an iterative process that refines approximations for a root. Starting with an initial guess \(x_{0}​\), the method uses the formula:

\(x_{n+1}=x_{n}​−\frac{f(x_{n} )}{f{}'(x_{n}) }\)

to approach a solution. Each iteration minimizes the error, gradually converging to a root.

Example: Solving \(x^{3}−x−1=0\)

Start with an estimate,\(x_{0}​=1\).

Calculate:\(f(x_{0}​​)=1^{3}−1−1=−1,{f{}'(x_{0}) } =3(1)^{2}−1=2\)

Using the formula:\(x_{1}​​=x_{0}​−\frac{f(x_{0} )}{f{}'(x_{0}) } =1−\frac{-1}{2} =1.5\)

Repeat the process with \(x_{1}​=1.5\), refining the root further. After a few iterations, the root converges to approximately \(x\approx 1.325\).

Graphical Assistance

Desmos or graphing calculators provide visual displays that depict polynomial curves, noting where they cross over into real roots of polynomials (x-axes). Such visual estimates make finding suitable starting points for numerical methods like Newton's Method easier while decreasing guesswork and increasing efficiency.

Applications of Cubic Equation Factorization

Cubic equations find practical applications across various disciplines. Below are three examples, each from a different field, illustrating how solving and factorizing cubic equations provides pivotal insights.

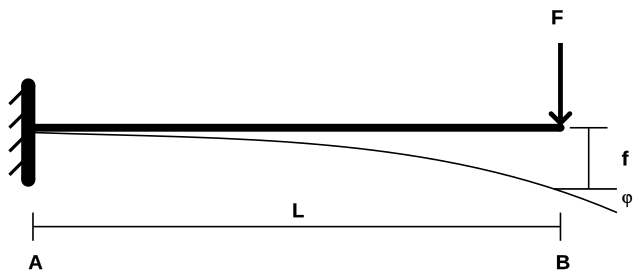
Engineering: Beam Deflection in Structural Analysis

In structural engineering, analyzing the deflection of a beam under a load often results in a cubic equation. For instance, consider a load distribution causing deflection governed by the equation:

\(x^{3}−3x^{2}+2x=0\)

Factorizing it as:

x(x−1)(x−2)=0

indicates critical points (x=0,x=1,x=2) where the beam's deflection or internal stresses undergo significant changes. These roots help engineers identify necessary reinforcement locations to prevent structural failure.

Business: Maximizing Profit

In economics, a company's profit function often follows a cubic relationship due to factors like diminishing returns. For example, the profit function:

\(P(x)=−2x^{3}+9x^{2}−12x+5\)

can be factorized to determine critical points where profit peaks or begins to decline. Factoring and solving reveal these points, guiding strategies for optimizing production or pricing to achieve maximum profitability while avoiding losses.

Physics: Modeling Fluid Flow

In fluid dynamics, the relationship between pressure, flow rate, and resistance in nonlinear systems often leads to cubic equations. For example, a flow system might be characterized by:

\(Q(x)=x^{3}−6x^{2}+11x−6=0\)

By factorizing this equation as:

(x−1)(x−2)(x−3)=0,

the roots (x=1,2,3) represent critical flow rates where pressure or turbulence changes drastically. This helps engineers optimize design to ensure stable and efficient fluid transport.

Conclusion

Factorizing cubic equations is an indispensable skill with wide-reaching implications across mathematics, science, and applied fields. By mastering this process, you gain access to tools for locating roots, simplifying expressions, and comprehending the behavior of systems represented by cubic models. By exploring various techniques -- special cases, grouping polynomials in divisional form (including numeric approximations of roots ), numerical approximation methods, as well as complex root handling -- you now possess all of the skills needed to confidently confront cubic equations from different directions!

Beyond solving equations mechanically, advanced concepts like graphical interpretations and real-world applications deepen our understanding. From structural analyses in engineering to optimizing business operations optimizations, cubic equations provide insights that are crucial in solving complex issues and driving innovation forward. Through practice and visualization techniques, factorization techniques may become intuitive over time, giving you the confidence to explore deeper mathematical challenges.

Reference:

https://artofproblemsolving.com/wiki/index.php/Vieta%27s_formulas?srsltid=AfmBOorm5Z0LjXcBpHMiviP0Ce_HdKcTLWn6q2U033rMaT2oisb11Kr8

https://www.sciencedirect.com/science/article/pii/S0377042700004350

https://www.researchgate.net/publication/360626977_Some_Applications_of_Cubic_Equations_in_Engineering