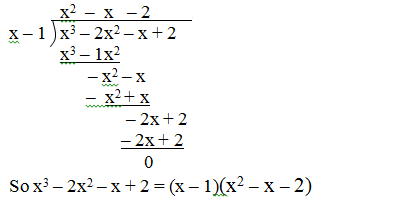Cómo Factorizar una Ecuación Cúbica

¿Qué es una Ecuación Cúbica?

Definición y Forma Estándar

Las ecuaciones cúbicas pertenecen a la categoría de polinomios: expresiones que involucran potencias de una variable desconocida. Como su nombre sugiere, una ecuación cúbica es un polinomio de grado tres, lo que indica que la potencia más alta de la variable desconocida (x) es tres. Tal ecuación se expresa en su forma estándar como:

\(ax^{3} + bx^{2} + cx + d = 0\),

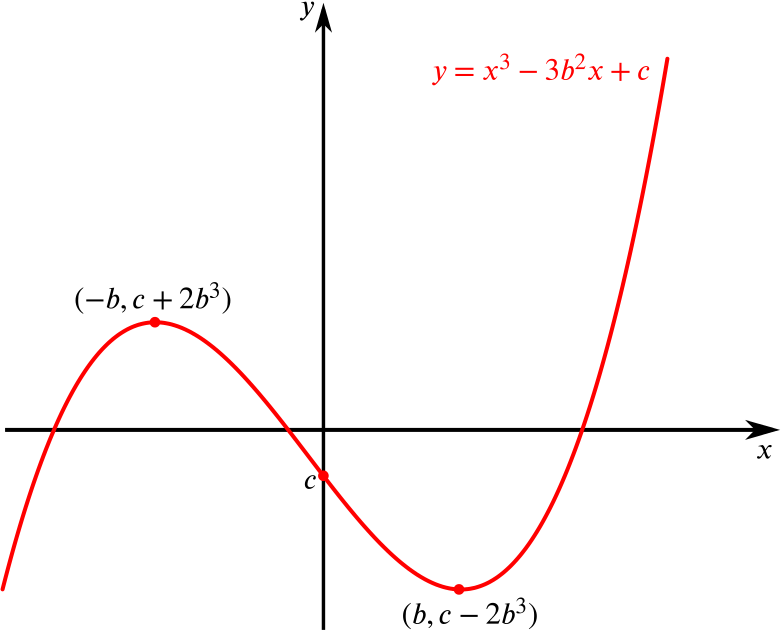
En este contexto, a, b, c y d son constantes, y \(a \ne 0\) porque sin el término cúbico, la ecuación dejaría de ser una ecuación cúbica. El grado de una ecuación le permite contener hasta tres raíces, reales o complejas. Estas raíces sirven como el núcleo de su solución al representar donde los polinomios intersectan los gráficos del eje x.

Raíces Reales y Raíces Complejas

Según el Teorema Fundamental del Álgebra, a toda ecuación cúbica se le garantiza al menos una raíz real. Sin embargo, la distribución de las raíces restantes depende de los coeficientes de la ecuación. Después de encontrar una raíz real, el cúbico a menudo puede reducirse a un cuadrático, cuyas raíces podrían ser reales o un par de conjugados complejos. Si las tres raíces de una ecuación cúbica son reales, su gráfico cruzará el eje x en tres puntos distintos; de lo contrario, intersecta una vez con una "forma ovalada" creada por raíces imaginarias que exhiben "torsión".

Encontrar raíces reales o complejas a menudo depende del uso de técnicas de factorización efectivas que dividen una ecuación cúbica en componentes más simples.

Importancia de la Factorización

La factorización de ecuaciones cúbicas implica descomponer polinomios en sus términos componentes - factores lineales y cuadráticos combinados - para simplificar la búsqueda de las raíces de cada polinomio. Una vez factorizado, cada raíz corresponde con un factor de este conjunto; una vez factorizado nuevamente, cada raíz corresponde con raíz(es) específica(s). Además, la factorización ayuda a entender las intersecciones y los puntos de inflexión del gráfico correspondiente a la ecuación cúbica.

Un ingeniero que analiza fuerzas de equilibrio en una estructura podría necesitar factorizar una ecuación cúbica que represente la distribución de carga para calcular sus raíces; la factorización simplifica estos cálculos y permite una determinación más precisa de los puntos críticos de estrés. Además, las relaciones de beneficio/costo de un negocio suelen exhibir un comportamiento no lineal, proporcionando a la factorización cúbica información valiosa sobre puntos clave como puntos de equilibrio o decisiones de precios óptimas.

La factorización ofrece más que aplicaciones prácticas; proporciona una visión matemática más profunda. La factorización revela simetrías, relaciones entre coeficientes y raíces, y análisis del comportamiento de sistemas complejos. El dominio de la factorización cúbica conecta el entendimiento teórico con la resolución de problemas del mundo real: habilidades esenciales en matemáticas, ciencia y más allá.

Métodos para Factorizar Ecuaciones Cúbicas

La factorización de ecuaciones cúbicas implica descomponer un polinomio cúbico en componentes más simples, generalmente factores lineales y cuadráticos, utilizando varias estrategias. Esta técnica puede descubrir raíces de una ecuación, simplificar expresiones complejas, analizar su comportamiento y descubrir raíces ocultas de polinomios. Discutimos algunas estrategias a continuación, incluyendo casos especiales de agrupación de factores lineales mediante la división y técnicas avanzadas; cada una tiene su propia aplicabilidad dependiendo de la estructura de una ecuación.

Casos Especiales de Ecuaciones Cúbicas

Reconocer ciertas ecuaciones cúbicas tiene la ventaja de facilitar la factorización; estar al tanto de tales patrones ahorrará tanto tiempo como energía en los esfuerzos de factorización.

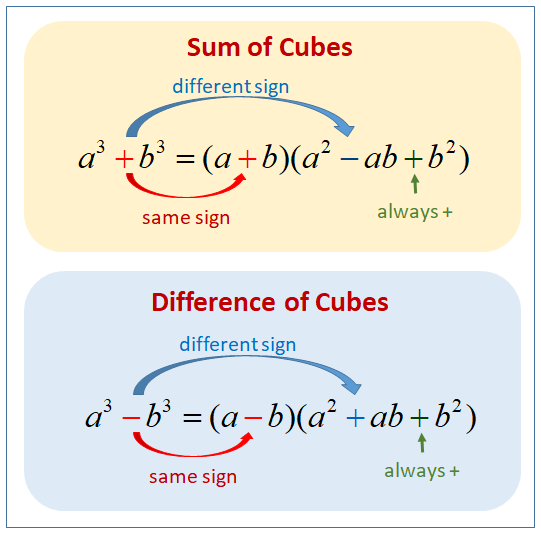
Suma y Diferencia de Cubos

Las ecuaciones que son sumas o diferencias de cubos perfectos se pueden factorizar utilizando las siguientes identidades algebraicas:

\(a^{3} +b^{3} =(a+b)(a^{2}−ab+b^{2})\)

\(a^{3}−b^{3}=(a−b)(a^{2}+ab+b^{2})\)

Estas fórmulas se aplican directamente cuando los términos cúbicos se pueden expresar como cubos perfectos. Los signos en los factores pueden recordarse utilizando el mnemotécnico "SOAP":

S igual al signo original en el primer factor,

Opuesto en el término medio del factor cuadrático,

Asiempre

Positivo en el último término.

Ejemplo 1: Suma de Cubos

Factorizar x^{3}+27:

x^{3}+27=x^{3}+3^{3}=(x+3)(x^{2}−3x+9)

Ejemplo 2: Diferencia de Cubos

Factorizar x^{3}−8:

x^{3}−8=x^{3}−2^{3}=(x−2)(x^{2}+2x+4)

Estas formas son particularmente comunes tanto en cálculos algebraicos como en aplicaciones del mundo real.

Formas Cúbicas Puras Sin Términos Lineales

A veces, las ecuaciones cúbicas carecen de ciertos términos intermedios, apareciendo en la forma simplificada \(ax^{3}+d=0\). Estas pueden ser factorizadas extrayendo directamente factores comunes.

Ejemplo: Factorizar \(x^{3}−9x=0\):

Extraer el factor común x:

\(x(x^{2}−9)=0\)

Factorizar el cuadrático resultante:

x(x−3)(x+3)=0

Perspectiva Gráfica:

Para tales ecuaciones, el gráfico cúbico se interseca con el eje x en x=0 y las otras raíces (por ejemplo, −3 y 3 en el ejemplo anterior). La factorización revela estos puntos directamente y simplifica cálculos posteriores.

H3: Factorización mediante Agrupación

Cuando una ecuación cúbica no encaja en identidades estándar o formas, el método de agrupación a menudo puede aplicarse. La agrupación reorganiza y empareja términos en la ecuación cúbica, permitiendo una factorización parcial paso a paso.

Pasos para la Factorización mediante Agrupación:

Divide los términos en dos grupos: Divide la ecuación en dos pares de términos que sugieran un factor común.

Factoriza cada grupo individualmente: Extrae el mayor factor común para cada grupo.

Combina los factores comunes: Si ambos grupos comparten un factor binomial común, extráelo.

Ejemplo: Factorizar \(2x^{3}−3x^{2}−2x+3\):

Agrupa términos:

\((2x^{3}−3x^{2})+(−2x+3)\)

2. Extraer factores comunes de cada grupo:

\(x^{2}(2x−3)−1(2x−3)\)

3. Combina el factor binomial común:

\((2x−3)(x^{2}−1)\)

4. Además, factoriza si es posible:

(2x−3)(x−1)(x+1)

Este método es eficaz para ecuaciones donde los términos pueden emparejarse naturalmente para revelar un binomio común. Puedes intentar más ejercicios en banco de preguntas sobre ecuaciones.

Usando Factores Lineales para Encontrar Factores Cuadráticos

Encontrar una raíz real y usarla para deducir otros factores para ecuaciones cúbicas generales que no siguen patrones particulares o agrupamientos es esencial al resolver ecuaciones cúbicas generales. Este método utiliza tanto el teorema del resto como la división de polinomios.

Paso 1: Usa el Teorema del Resto

De acuerdo con el Teorema del Resto, si P(a)=0, entonces (x−a) sirve como factor de P(x). Empieza adivinando raíces potenciales probando valores lógicos como ±1,±2,±3, etc.

Paso 2: Realiza la Divisiónde Polinomios

Una vez identificada una raíz, divide el polinomio cúbico por su factor lineal (x-a). Después de hacer esto, se utiliza la división larga de polinomios o la división sintética para localizar y extraer cualquier factor cuadrático restante.

Ejemplo: Factorizar \(x^{3}−6x^{2}+11x−6\):

Adivina raíces potenciales (x=1, x=2, etc.) y prueba:

\(P(1)=1^{3}−6(1^{2})+11(1)−6=0\) (Raíz encontrada en x=1).

Divide \(x^{3}−6x^{2}+11x−6\) por (x−1):

\(\frac{x^{3}−6x^{2}+11x−6}{x-1} =x^{2}−5x+6\)

Factoriza el cuadrático:

\(x^{2}−5x+6=(x−2)(x−3)\)

Combina todos los factores:

\(x^{3}−6x^{2}+11x−6=(x−1)(x−2)(x−3)\)

Este método es particularmente útil para ecuaciones con raíces enteras y asegura que todo el proceso de factorización sea sistemático.

Métodos Avanzados para Factorizar Ecuaciones Cúbicas

Cuando no hay una raíz obvia o la ecuación involucra coeficientes difíciles, entran en juego técnicas avanzadas:

Usando las Fórmulas de Vieta

Las soluciones de la ecuación cúbica \(ax^{3}+bx^{2}+cx+d=0\) cumplen con las siguientes relaciones:

La suma de las raíces: \(r_{1} +r_{2} +r_{3} =−b/a\),

La suma de los productos de parejas: \(r_{1}​r_{2}​+r_{2}​r_{3}​+r_{1}​r_{3}​=c/a\),

El producto de las raíces: \(r_{1}r_{2}r_{3}​=−d/a\).

Combinando este conocimiento, a veces se pueden identificar patrones específicos en las raíces, llevando a

Aplicaciones de la Factorización de Ecuaciones Cúbicas

Las ecuaciones cúbicas encuentran aplicaciones prácticas en diversas disciplinas. A continuación se presentan tres ejemplos, cada uno de un campo diferente, que ilustran cómo la resolución y factorización de ecuaciones cúbicas proporcionan ideas clave.

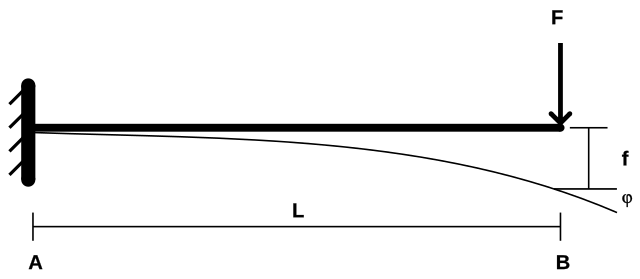
Ingeniería: Deflexión de Vigas en Análisis Estructural

En ingeniería estructural, el análisis de la deflexión de una viga bajo una carga a menudo resulta en una ecuación cúbica. Por ejemplo, considere una distribución de carga que provoca una deflexión regida por la ecuación:

\(x^{3}−3x^{2}+2x=0\)

Factorizándola como:

x(x−1)(x−2)=0

indica puntos críticos (x=0,x=1,x=2) donde la deflexión de la viga o las tensiones internas experimentan cambios significativos. Estas raíces ayudan a los ingenieros a identificar las ubicaciones necesarias de refuerzo para prevenir fallos estructurales.

Negocios: Maximización de Beneficios

En economía, la función de ganancias de una compañía a menudo sigue una relación cúbica debido a factores como los rendimientos decrecientes. Por ejemplo, la función de ganancias:

\(P(x)=−2x^{3}+9x^{2}−12x+5\)

puede ser factorizada para determinar los puntos críticos donde las ganancias alcanzan su pico o comienzan a disminuir. La factorización y resolución revelan estos puntos, guiando estrategias para optimizar la producción o precios para lograr la máxima rentabilidad evitando pérdidas.

Física: Modelado del Flujo de Fluidos

En dinámica de fluidos, la relación entre presión, caudal y resistencia en sistemas no lineales a menudo lleva a ecuaciones cúbicas. Por ejemplo, un sistema de flujo podría caracterizarse por:

\(Q(x)=x^{3}−6x^{2}+11x−6=0\)

Al factorizar esta ecuación como:

(x−1)(x−2)(x−3)=0,

las raíces (x=1,2,3) representan caudales críticos donde la presión o la turbulencia cambian drásticamente. Esto ayuda a los ingenieros a optimizar el diseño para garantizar un transporte de fluidos estable y eficiente.

Conclusión

Factorizar ecuaciones cúbicas es una habilidad indispensable con implicaciones de gran alcance en matemáticas, ciencia y campos aplicados. Al dominar este proceso, obtienes herramientas para localizar raíces, simplificar expresiones y comprender el comportamiento de sistemas representados por modelos cúbicos. Al explorar diversas técnicas — casos especiales, agrupar polinomios en forma divisional (incluyendo aproximaciones numéricas de raíces), métodos de aproximación numérica, así como el manejo de raíces complejas — ahora posees todas las habilidades necesarias para enfrentarte a ecuaciones cúbicas desde diferentes perspectivas con confianza.

Más allá de resolver ecuaciones mecánicamente, conceptos avanzados como interpretaciones gráficas y aplicaciones en el mundo real profundizan nuestra comprensión. Desde análisis estructurales en ingeniería hasta la optimización de operaciones empresariales, las ecuaciones cúbicas proporcionan ideas cruciales para resolver problemas complejos y avanzar en la innovación. A través de la práctica y técnicas de visualización, las técnicas de factorización pueden volverse intuitivas con el tiempo, brindándote la confianza para explorar desafíos matemáticos más profundos.

Referencia:

https://artofproblemsolving.com/wiki/index.php/Vieta%27s_formulas?srsltid=AfmBOorm5Z0LjXcBpHMiviP0Ce_HdKcTLWn6q2U033rMaT2oisb11Kr8

https://www.sciencedirect.com/science/article/pii/S0377042700004350

https://www.researchgate.net/publication/360626977_Some_Applications_of_Cubic_Equations_in_Engineering