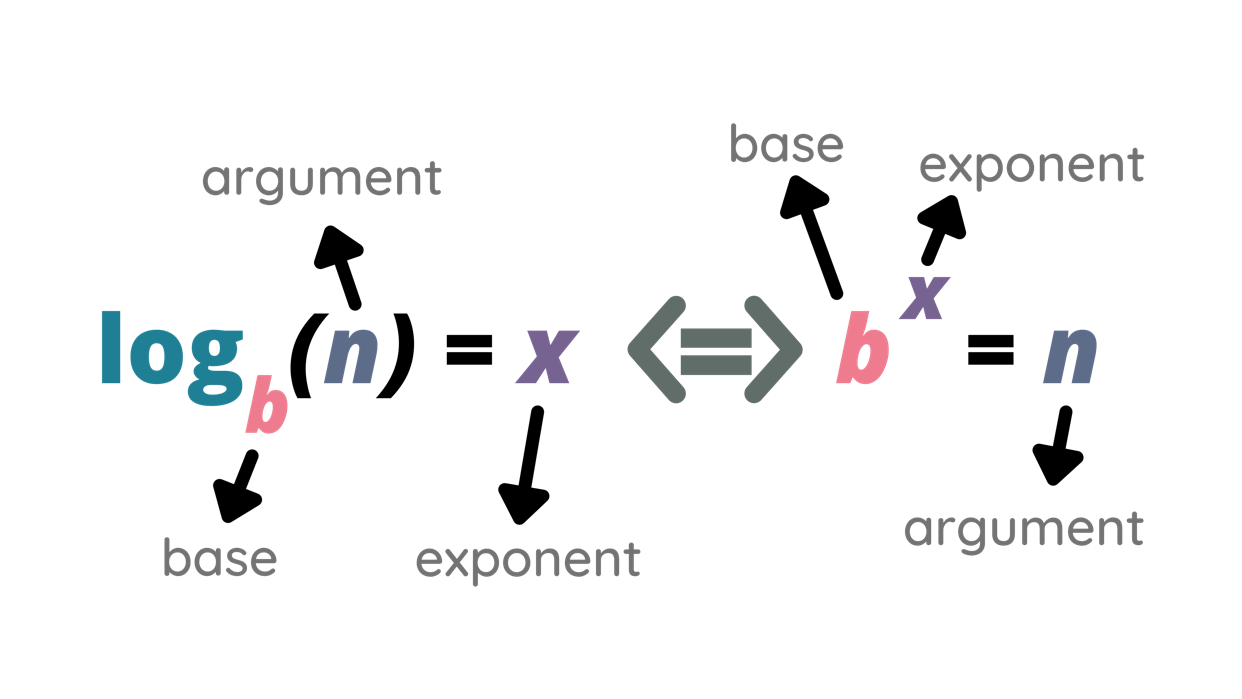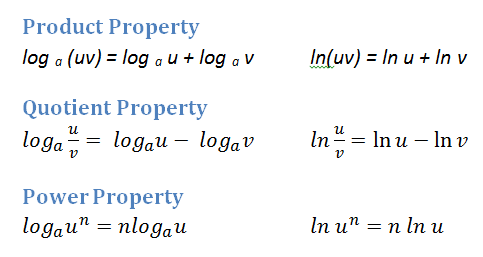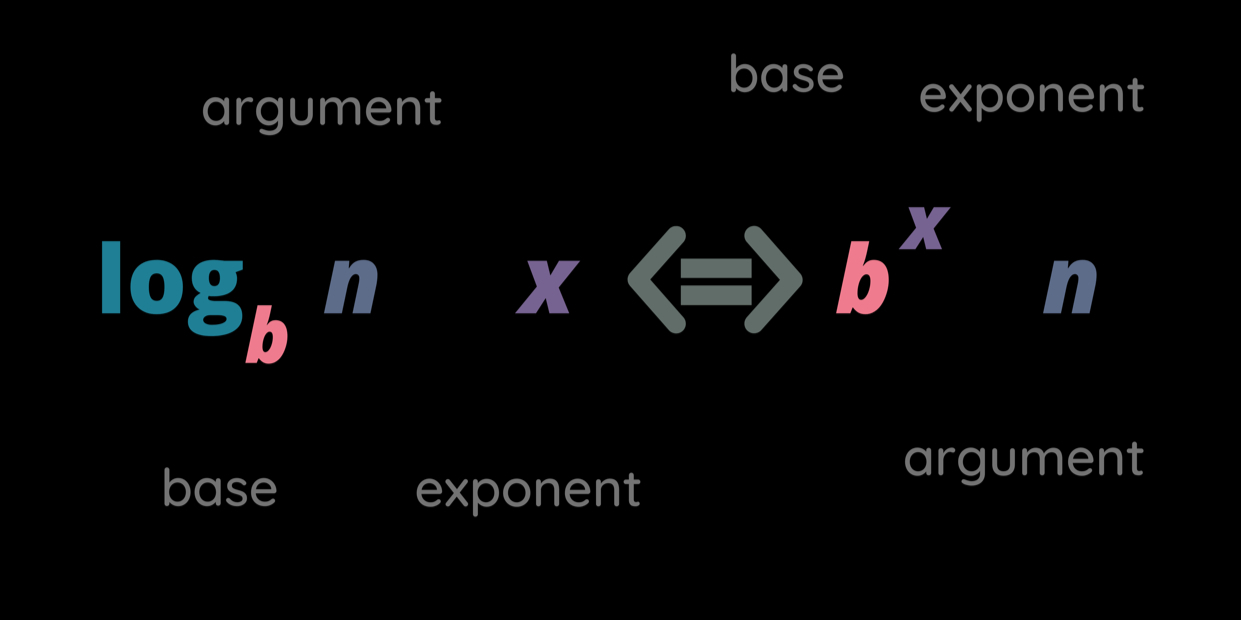How to Solve Logarithmic Equations?

The Basics of Logarithms

Before diving into the methods for solving logarithmic equations, it's crucial to understand what logarithms are and their foundational properties.

What Are Logarithms?

Logarithms are the inverse operations of exponentials, meaning they answer the question: "To what power must the base be raised to produce a given result?"

For example:

In logarithmic terms: \(\log_{a}{x} = y\)

In exponential terms: \(a^{y} = x\)

Here:

a is the base of the logarithm,

y is the exponent (or logarithm), and

x is the result.

For instance, \(\log_{2}{8} = 3\) tells us that \(2^{3} = 8\) .

Rules for Bases and Arguments

Logarithms are defined under specific conditions:

Base constraints: The base (a) must be greater than 0 and not equal to 1:

a > 0, a ≠ 1.

Argument constraints : The argument (x) must be strictly positive:

x > 0.

These constraints are vital since logarithmic and exponential functions are undefined otherwise.

Fundamental Properties of Logarithms

Solving logarithmic equations requires mastery of their core properties. Following their rules will help make solving logarithmic expressions simpler, enabling equations to be simplified or altered more efficiently.

The Three Core Properties

Product Rule 

The logarithm of a multiplication is equivalent to the addition of the logarithms:

\(\log_{a}{M x N} = \log_{a}{M} + \log_{a}{N}\)

Example :

\(\log_{5}{10 x 3} = \log_{5}{10} + \log_{5}{3}→ Simplifies to \log_{5}{30} .\)

Quotient Rule

The logarithm of a division is equal to the subtraction of the logarithms:

\(\log_{a}{M / N} = \log_{a}{M} − \log_{a}{N}\)

Example :

\(\log_{2}{8/2} = \log_{2}{8} − \log_{2}{2} → Simplifies to \log_{2}{4} .\)

H4: Power Rule

The logarithm of a number exponentiated by a power is equivalent to the power times the logarithm of the base:

\(\log_{a}{M^{p}} = p × \log_{a}{M}\)

Example :

\(\log_{3}{9^{2}} = 2 × \log_{3}{9} → Simplifies to 2 × 2 = 4 .\)

Intuitive Way to Remember

Logarithmic rules can be thought of like weights on a scale:

The product rule multiplies weights together to represent multiplication, whilst division is shown through subtraction from one weight, whilst power rules double or triple weights and indicate repeated use.

Visuals like these can make complex transformations simpler to remember and apply, helping users intuitively grasp logarithmic manipulations more readily.

Step-by-Step Methods for Solving Logarithmic Equations

Solving logarithmic equations involves identifying the structure of the equation and applying the appropriate techniques. Below are various methods tailored to common types of logarithmic equations.

Method 1 - Solving Basic Single-Logarithmic Equations

Format

\(\log_{a}{M}=b\)

Steps

Rewrite the equation in exponential form:

\(\log_{a}{M}=b → a^{b} = M\)

Solve for M.

Example

Solve \(\log_{3}{81}=x:\)

Rewrite as \(3^{x} = 81\).

Solve: x = 4 (since\(3^{4} = 81\)).

Tip: Always check that the solution fits the logarithmic domain, ensuring the base and argument are positive.

Method 2 - Solving by Using the Logarithmic Product Rule

Format 

\(\log_{a}{M}+ \log_{a}{N} = b\)

Steps

Combine logarithmic terms using the product rule:

\(\log_{a}{M} + \log_{a}{N} → \log_{a}{M x N} .\)

Rewrite the equation in exponential form:

\(a^{b} = M × N\) .

Solve for the unknown value.

Example

Solve \(\log_{2}{x} + \log_{2}{x-3} = 5\) :

Combine logs: \(\log_{2}{x(x-3)} = 5\) .

Rewrite: \(2^{5} = x(x − 3)\) .

Simplify: \(32 = x^{2} − 3x → x^{2} − 3x − 32 = 0\) .

Solve the quadratic equation: x = 8, x = -4 (discard x = -4 due to domain constraints).

Solution: x = 8 satisfies the equation.

Method 3 - Solving by Using the Logarithmic Quotient Rule

Format

\(\log_{a}{M} − \log_{a}{N} = b\)

Steps

Use the quotient rule to combine terms:

\(\log_{a}{M} − \log_{a}{N} → \log_{a}{M/N}.\)

Rewrite the logarithmic equation in exponential form:

\(a^{b}= M / N\) .

Solve for the unknown variable.

Example

Solve \(\log_{4}{2x+5} − \log_{4}{x − 3} = 2\):

Combine logs: \(\log_{4}{2x+5/ (x − 3)}= 2\) .

Rewrite in exponential form: \(4^{2} = (2x + 5) / (x − 3)\) .

Solve: 16(x − 3) = 2x + 5 → 16x − 48 = 2x + 5 → 14x = 53 → x = 53/14 .

Method 4 - Equating Two Logarithmic Expressions

Format

\(\log_{a}{M} = \log_{a}{N}\)

Steps

If both sides of the equation have the same base logarithm, equate their arguments:

M = N.

Solve for x.

Example

Solve \(\log_{5}{2x + 1} = \log_{5}{x + 4}\) :

Equate arguments: 2x + 1 = x + 4 .

Solve: x = 3.

This method works because the equality of logarithms implies the equality of their contents.

Method 5 - Solving System-Based Logarithmic Equations

System-based problems involve multiple logarithmic rules applied throughout the equation.

Example

Solve \(\log_{2}{x + 2} + \log_{2}{3x + 5} = \log_{2}{5x − 7}\) :

Combine left-hand side:\(\log_{2}{(x + 2)(3x + 5)} = \log_{2}{5x − 7}\) .

Equate arguments: (x + 2)(3x + 5) = 5x − 7 .

Expand: \(3x^{2} + 11x + 10 = 5x − 7 → 3x^{2} + 6x + 17 = 0\) .

Solve for x: Using the quadratic formula gives the appropriate values.

You can practice in question bank to test whether you've truly mastered it.

Common Mistakes and How to Avoid Them

Understanding logarithmic functions is essential in advanced mathematics, but they can be tricky to work with. Students often encounter specific pitfalls when solving logarithmic equations or simplifying expressions. Below are common mistakes and practical advice to avoid them.

Misapplying Logarithmic Properties

A common misconception arises when students misapply the basic properties and rules of logarithms. For example, a frequent mistake is assuming that the logarithm of a sum is equal to the sum of the logarithms:

Incorrect:

\(\log_{a}{x + y} = \log_{a}{x} + \log_{a}{y}\)

This is fundamentally wrong because it violates the product rule, which only applies to the product of terms, not their sum. The correct rule states:

\(\log_{a}{x * y} = logₐ(x) + logₐ(y)\)

To avoid this error, revisit and memorize the core logarithmic rules, such as the power, product, and quotient rules. Practice applying them carefully in different contexts to internalize their correct usage.

Forgetting Domain Restrictions

Failing to take into account the domain restrictions of logarithmic functions is another significant mistake since their arguments must always be positive; otherwise, \(\log_{a}{x}\) becomes undefined at x ≤ 0. However, logarithms for non-positive numbers don't exist within the real number system and must, therefore, remain undefined for that particular x value.

An error in this rule could result in invalid solutions to equations, for instance resulting in results such as x = -3 that don't satisfy logarithmic functions. Always double-check that solutions fall within their valid range before concluding an equation or solving one with logarithms.

Tip: Before solving equations or simplifying, be sure to state their domain restrictions explicitly; this step will enable you to detect and eliminate unnecessary solutions more efficiently.

By avoiding these common errors in handling logarithms more confidently and maintaining mathematical precision in your solutions, you will increase confidence when working with logarithms and increase mathematical precision in solutions.

Application of Logarithms

Logarithms are an indispensable mathematical tool used in numerous fields to solve exponential growth or decay issues, providing solutions to complex multiplicative relationships by turning them into simpler additive ones and thus offering insight into real world phenomena such as finance, biology, computing and physics. Let us look at specific examples in these sectors to demonstrate its usefulness and importance.

Finance

Logarithms are used to calculate the time it takes for investments to grow under compound interest. For instance, using the formula \(t=\frac{\log{(\frac{F}{P}) } }{\log(1+r)}\), where P is the principal, F is the future value, and r is the interest rate, you can determine how long it will take to double an initial investment of $1,000 at a 5% annual interest rate. The computation shows it will take approximately 14.2 years. This ability to precisely model growth over time is fundamental for long-term financial planning and decision-making.

Biology

Logarithms provide an effective means of modeling population dynamics where resources are limited, leading to slower population growth over time. Logarithmic models like logistic growth models utilize logarithmic relations in order to estimate when populations will stabilize as they approach carrying capacities within an environment and scientists can use these relationships more easily predict trends and design effective conservation strategies that maintain ecological balance.

Computing

Logarithms provide the basis for measuring algorithm efficiency, particularly with processes like binary search. Binary search operates with an \(O(\log{n})\), meaning its step count scales logarithmically with dataset size; for instance, searching through 1 Million items via binary search would only require approximately 20 comparisons - an efficiency essential in managing vast quantities of information in fields like programming, data science, and artificial intelligence.

Physics

Logarithms provide an efficient means of simplifying calculations that involve exponential decay, such as radioactive half-life calculations. Radiocarbon dating uses the logarithmic formula \(t=\frac{\ln_{}{2} }{\lambda }\) to accurately gauge the age of artifacts dating from ancient civilizations based on the constant decay. Archaeologists and physicists alike rely on radiocarbon dating technology to accurately date materials and provide critical insights into historical or geological timelines.

Logarithms provide an interdisciplinary basis for solving exponential relationship-based problems efficiently, offering meaningful predictions, trend analyses and equation solutions in both theoretical and applied settings. Their usefulness lies both theoretically and practically - thus underscoring their importance both academically and practically.

Conclusion

Logarithmic equations may initially seem complex; however, with proper knowledge and an organized approach to problem-solving techniques, they become manageable and approachable. Logarithms provide a structured way of unraveling exponential relationships by isolating variables and interpreting trends; by mastering their fundamental rules as well as domain restrictions, you can confidently simplify and solve equations while avoiding common pitfalls.

Logarithms have many real-world applications beyond mathematics, from modeling population growth and algorithm efficiency analysis to financial investments or analysis of population patterns. Logarithms simplify exponential problems so it's possible to predict outcomes and draw meaningful conclusions across disciplines with ease; with practice, logarithms become not only mathematical tools but a gateway into understanding and solving practical challenges with ease.

Reference:

https://www.vaia.com/en-us/textbooks/math/contemporary-precalculus-5-edition/chapter-5/problem-65-deal-with-the-compound-interest-formula-ap1rt-whi/

https://www.sciencedirect.com/science/article/pii/S0303264724002272

https://www.math.purdue.edu/~egbertn/fa2016/notes/lesson21.pdf