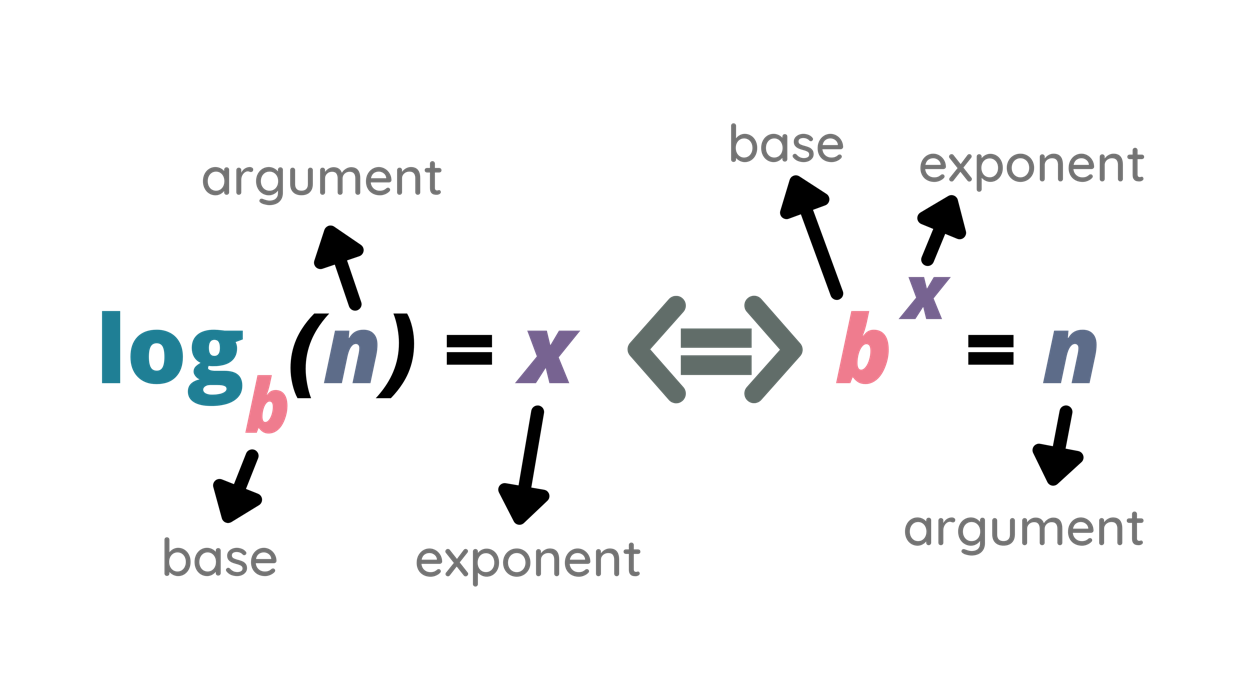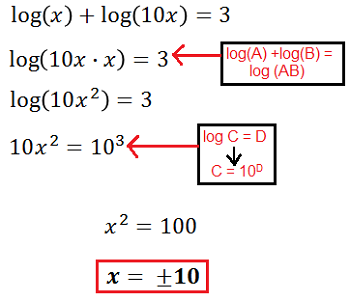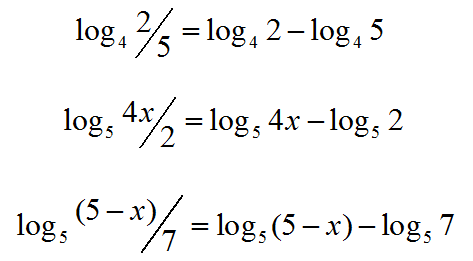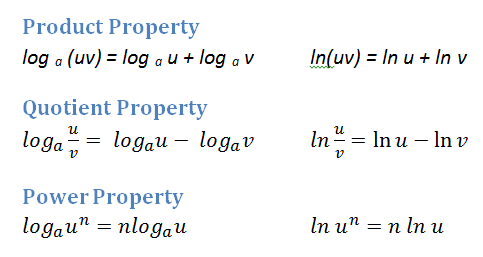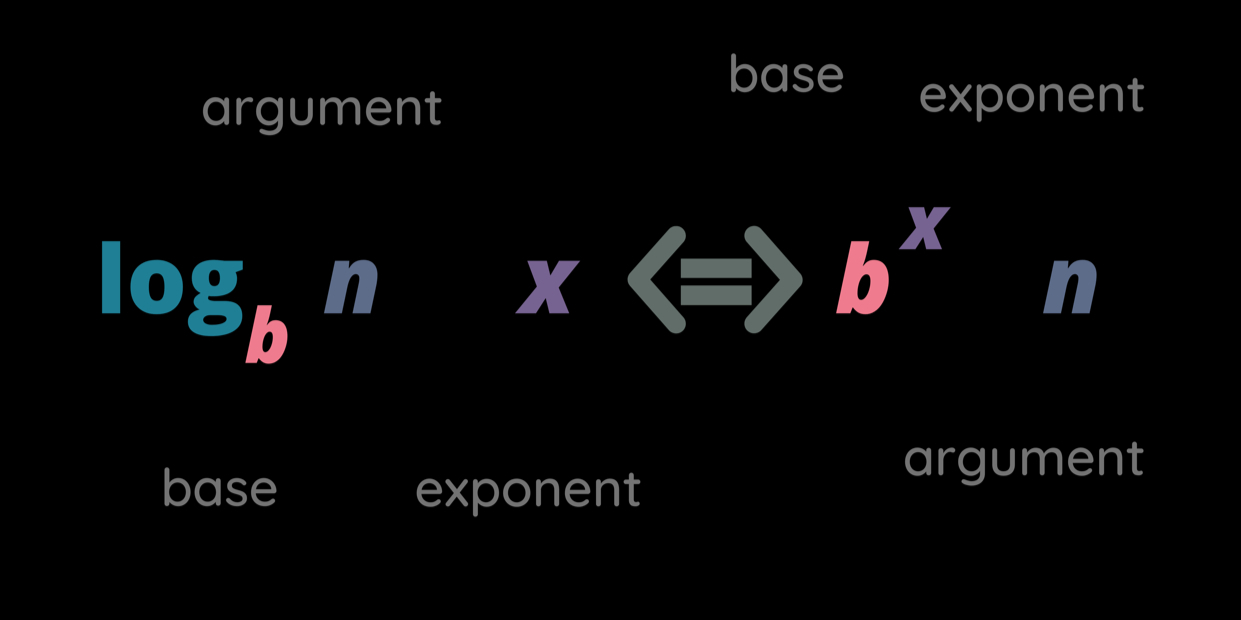Cómo Resolver Ecuaciones Logarítmicas

Los conceptos básicos de los logaritmos

Antes de adentrarnos en los métodos para resolver ecuaciones logarítmicas, es crucial entender qué son los logaritmos y sus propiedades fundamentales.

¿Qué son los logaritmos?

Los logaritmos son las operaciones inversas de las exponenciales, lo que significa que responden a la pregunta: "¿A qué potencia debe elevarse la base para obtener un resultado dado?"

Por ejemplo:

En términos logarítmicos: \(\log_{a}{x} = y\)

En términos exponenciales: \(a^{y} = x\)

Aquí:

a es la base del logaritmo,

y es el exponente (o logaritmo), y

x es el resultado.

Por ejemplo, \(\log_{2}{8} = 3\) nos dice que \(2^{3} = 8\) .

Reglas para bases y argumentos

Los logaritmos están definidos bajo condiciones específicas:

Restricciones de la base: La base (a) debe ser mayor que 0 y no igual a 1:

a > 0, a ≠ 1.

Restricciones del argumento : El argumento (x) debe ser estrictamente positivo:

x > 0.

Estas restricciones son vitales ya que de otro modo las funciones logarítmicas y exponenciales no están definidas.

Propiedades Fundamentales de los Logaritmos

Resolver ecuaciones logarítmicas requiere el dominio de sus propiedades fundamentales. Seguir sus reglas ayudará a facilitar la resolución de expresiones logarítmicas, permitiendo que las ecuaciones se simplifiquen o se modifiquen de manera más eficiente.

Las Tres Propiedades Básicas

Regla del Producto 

El logaritmo de una multiplicación es equivalente a la suma de los logaritmos:

\(\log_{a}{M x N} = \log_{a}{M} + \log_{a}{N}\)

Ejemplo :

\(\log_{5}{10 x 3} = \log_{5}{10} + \log_{5}{3}→ Se simplifica a \log_{5}{30} .\)

Regla del Cociente

El logaritmo de una división es igual a la resta de los logaritmos:

\(\log_{a}{M / N} = \log_{a}{M} − \log_{a}{N}\)

Ejemplo :

\(\log_{2}{8/2} = \log_{2}{8} − \log_{2}{2} → Se simplifica a \log_{2}{4} .\)

Regla de la Potencia

El logaritmo de un número elevado a una potencia es equivalente a la potencia multiplicada por el logaritmo de la base:

\(\log_{a}{M^{p}} = p × \log_{a}{M}\)

Ejemplo :

\(\log_{3}{9^{2}} = 2 × \log_{3}{9} → Se simplifica a 2 × 2 = 4 .\)

Forma Intuitiva de Recordar

Las reglas logarítmicas pueden pensarse como pesas en una balanza:

La regla del producto multiplica las pesas juntas para representar la multiplicación, mientras que la división se muestra restando de una pesa, mientras que las reglas de potencia duplican o triplican las pesas e indican un uso repetido.

Visuales como estos pueden hacer que las transformaciones complejas sean más fáciles de recordar y aplicar, ayudando a los usuarios a comprender intuitivamente las manipulaciones logarítmicas de manera más rápida.

Métodos Paso a Paso para Resolver Ecuaciones Logarítmicas

Resolver ecuaciones logarítmicas implica identificar la estructura de la ecuación y aplicar las técnicas adecuadas. A continuación, se presentan varios métodos adaptados a los tipos comunes de ecuaciones logarítmicas.

Método 1 - Resolviendo Ecuaciones Básicas de Logaritmo Único

Formato

\(\log_{a}{M}=b\)

Pasos

Reescribir la ecuación en forma exponencial:

\(\log_{a}{M}=b → a^{b} = M\)

Resolver para M.

Ejemplo

Resolver \(\log_{3}{81}=x:\)

Reescribir como \(3^{x} = 81\).

Resolver: x = 4 (ya que\(3^{4} = 81\)).

Consejo: Siempre verificar que la solución se ajuste al dominio del logaritmo, asegurando que la base y el argumento sean positivos.

Método 2 - Resolviendo Usando la Regla del Producto Logarítmico

Formato 

\(\log_{a}{M} + \log_{a}{N} = b\)

Pasos

Combinar términos logarítmicos usando la regla del producto:

\(\log_{a}{M} + \log_{a}{N} → \log_{a}{M x N} .\)

Reescribir la ecuación en forma exponencial:

\(a^{b} = M × N\) .

Resolver para el valor desconocido.

Ejemplo

Resolver \(\log_{2}{x} + \log_{2}{x-3} = 5\) :

Combinar logaritmos: \(\log_{2}{x(x-3)} = 5\) .

Reescribir: \(2^{5} = x(x − 3)\) .

Simplificar: \(32 = x^{2} − 3x → x^{2} − 3x − 32 = 0\) .

Resolver la ecuación cuadrática: x = 8, x = -4 (descartar x = -4 debido a restricciones de dominio).

Solución: x = 8 satisface la ecuación.

Método 3 - Resolviendo Usando la Regla del Cociente Logarítmico

Formato

\(\log_{a}{M} − \log_{a}{N} = b\)

Pasos

Usar la regla del cociente para combinar términos:

\(\log_{a}{M} − \log_{a}{N} → \log_{a}{M/N}.\)

Reescribir la ecuación logarítmica en forma exponencial:

\(a^{b}= M / N\) .

Resolver para la variable desconocida.

Ejemplo

Resolver \(\log_{4}{2x+5} − \log_{4}{x − 3} = 2\):

Combinar logaritmos: \(\log_{4}{2x+5/ (x − 3)}= 2\) .

Reescribir en forma exponencial: \(4^{2} = (2x + 5) / (x − 3)\) .

Resolver: 16(x − 3) = 2x + 5 → 16x − 48 = 2x + 5 → 14x = 53 → x = 53/14 .

Método 4 - Igualando Dos Expresiones Logarítmicas

Formato

\(\log_{a}{M} = \log_{a}{N}\)

Pasos

Si ambos lados de la ecuación tienen el mismo logaritmo base, iguala sus argumentos:

M = N.

Resolver para x.

Ejemplo

Resolver \(\log_{5}{2x + 1} = \log_{5}{x + 4}\) :

Igualar argumentos: 2x + 1 = x + 4 .

Resolver: x = 3.

Este método funciona porque la igualdad de logaritmos implica la igualdad de sus contenidos.

Método 5 - Resolviendo Ecuaciones Logarítmicas Basadas en Sistemas

Los problemas basados en sistemas involucran múltiples reglas logarítmicas aplicadas a lo largo de la ecuación.

Ejemplo

Resolver \(\log_{2}{x + 2} + \log_{2}{3x + 5} = \log_{2}{5x − 7}\) :

Combinar lado izquierdo:\(\log_{2}{(x + 2)(3x + 5)} = \log_{2}{5x − 7}\) .

Igualar argumentos: (x + 2)(3x + 5) = 5x − 7 .

Expandir: \(3x^{2} + 11x + 10 = 5x − 7 → 3x^{2} + 6x + 17 = 0\) .

Resolver para x: Usando la fórmula cuadrática se obtienen los valores apropiados.

Puedes practicar en el banco de preguntas para comprobar si realmente lo has dominado.

Errores Comunes y Cómo Evitarlos

Entender las funciones logarítmicas es esencial en matemáticas avanzadas, pero pueden ser complicadas de manejar. Los estudiantes a menudo encuentran dificultades específicas al resolver ecuaciones logarítmicas o simplificar expresiones. A continuación se presentan errores comunes y consejos prácticos para evitarlos.

Aplicación Incorrecta de las Propiedades Logarítmicas

Un error común surge cuando los estudiantes aplican incorrectamente las propiedades y reglas básicas de los logaritmos. Por ejemplo, un error frecuente es asumir que el logaritmo de una suma es igual a la suma de los logaritmos:

Incorrecto:

\(\log_{a}{x + y} = \log_{a}{x} + \log_{a}{y}\)

Esto es fundamentalmente incorrecto porque viola la regla del producto, que solo se aplica al producto de términos, no a su suma. La regla correcta establece:

\(\log_{a}{x * y} = logₐ(x) + logₐ(y)\)

Para evitar este error, revisa y memoriza las reglas logarítmicas fundamentales, como las de potencia, producto y cociente. Practicar aplicándolas cuidadosamente en diferentes contextos para internalizar su uso correcto.

Olvidar las Restricciones de Dominio

No tener en cuenta las restricciones de dominio de las funciones logarítmicas es otro error significativo, ya que sus argumentos deben ser siempre positivos; de lo contrario, \(\log_{a}{x}\) se vuelve indefinido cuando x ≤ 0. Los logaritmos para números no positivos no existen dentro del sistema de números reales y, por lo tanto, deben permanecer indefinidos para ese valor particular de x.

Un error en esta regla podría resultar en soluciones inválidas para ecuaciones, por ejemplo, resultando en resultados como x = -3 que no satisfacen las funciones logarítmicas. Siempre verifica que las soluciones caigan dentro de su rango válido antes de concluir una ecuación o resolver una con logaritmos.

Consejo: Antes de resolver ecuaciones o simplificar, asegúrate de declarar explícitamente sus restricciones de dominio; este paso te permitirá detectar y eliminar soluciones innecesarias de manera más eficiente.

Al evitar estos errores comunes manejarás los logaritmos con más confianza y mantendrás la precisión matemática en tus soluciones, incrementando la confianza al trabajar con logaritmos y aumentando la precisión matemática en las soluciones.

Aplicación de los Logaritmos

Los logaritmos son una herramienta matemática indispensable utilizada en numerosos campos para resolver problemas de crecimiento o decrecimiento exponencial, proporcionando soluciones a complejas relaciones multiplicativas al convertirlas en relaciones aditivas más simples, ofreciendo así una visión de fenómenos del mundo real como las finanzas, la biología, la informática y la física. Veamos ejemplos específicos en estos sectores para demostrar su utilidad e importancia.

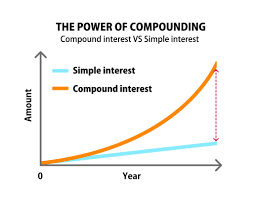
Finanzas

Los logaritmos se utilizan para calcular el tiempo que tarda una inversión en crecer bajo interés compuesto. Por ejemplo, usando la fórmula \(t=\frac{\log{(\frac{F}{P}) } }{\log(1+r)}\), donde P es el capital inicial, F es el valor futuro, y r es la tasa de interés, puedes determinar cuánto tiempo tomará duplicar una inversión inicial de $1,000 con una tasa de interés anual del 5%. El cálculo muestra que tomará aproximadamente 14.2 años. Esta capacidad para modelar con precisión el crecimiento en el tiempo es fundamental para la planificación financiera a largo plazo y la toma de decisiones.

Biología

Los logaritmos proporcionan un medio efectivo para modelar dinámicas poblacionales donde los recursos son limitados, lo que lleva a un crecimiento poblacional más lento con el tiempo. Modelos logarítmicos, como los modelos de crecimiento logístico, utilizan relaciones logarítmicas para estimar cuándo se estabilizarán las poblaciones a medida que se acercan a las capacidades de carga dentro de un entorno, y los científicos pueden usar estas relaciones para prever tendencias y diseñar estrategias de conservación efectivas que mantengan el equilibrio ecológico.

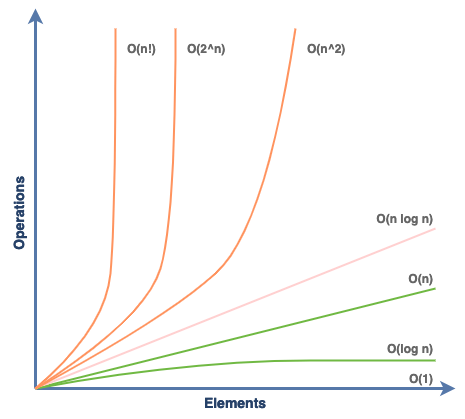
Informática

Los logaritmos proporcionan la base para medir la eficiencia de los algoritmos, particularmente con procesos como la búsqueda binaria. La búsqueda binaria opera con un \(O(\log{n})\), lo que significa que su número de pasos escala logarítmicamente con el tamaño del conjunto de datos; por ejemplo, buscar entre 1 millón de elementos a través de búsqueda binaria solo requeriría aproximadamente 20 comparaciones, una eficiencia esencial en la gestión de grandes cantidades de información en campos como la programación, la ciencia de datos y la inteligencia artificial.

Física

Los logaritmos proporcionan un medio eficiente para simplificar cálculos que involucran decaimiento exponencial, como los cálculos de vida media radiactiva. La datación por radiocarbono utiliza la fórmula logarítmica \(t=\frac{\ln_{}{2} }{\lambda }\) para calcular con precisión la edad de artefactos que datan de civilizaciones antiguas basándose en el decaimiento constante. Arqueólogos y físicos dependen de la tecnología de datación por radiocarbono para fechar materiales con precisión y proporcionar información crítica sobre cronologías históricas o geológicas.

Los logaritmos proporcionan una base interdisciplinaria para resolver problemas basados en relaciones exponenciales de manera eficiente, ofreciendo predicciones significativas, análisis de tendencias y soluciones de ecuaciones tanto en entornos teóricos como aplicados. Su utilidad reside tanto teórica como prácticamente, subrayando así su importancia tanto académica como práctica.

Conclusión

Las ecuaciones logarítmicas pueden parecer inicialmente complejas; sin embargo, con el conocimiento adecuado y un enfoque organizado hacia las técnicas de resolución de problemas, se vuelven manejables y accesibles. Los logaritmos proporcionan un método estructurado para desentrañar relaciones exponenciales al aislar variables e interpretar tendencias; al dominar sus reglas fundamentales, así como las restricciones del dominio, puedes simplificar y resolver ecuaciones con confianza mientras evitas errores comunes.

Los logaritmos tienen muchas aplicaciones en el mundo real más allá de las matemáticas, desde modelar el crecimiento poblacional y el análisis de la eficiencia de algoritmos hasta inversiones financieras o el análisis de patrones poblacionales. Los logaritmos simplifican problemas exponenciales, lo que permite predecir resultados y sacar conclusiones significativas a través de disciplinas con facilidad; con la práctica, los logaritmos se convierten no solo en herramientas matemáticas, sino en una puerta hacia la comprensión y resolución de desafíos prácticos con facilidad.

Referencia:

https://www.vaia.com/en-us/textbooks/math/contemporary-precalculus-5-edition/chapter-5/problem-65-deal-with-the-compound-interest-formula-ap1rt-whi/

https://www.sciencedirect.com/science/article/pii/S0303264724002272

https://www.math.purdue.edu/~egbertn/fa2016/notes/lesson21.pdf