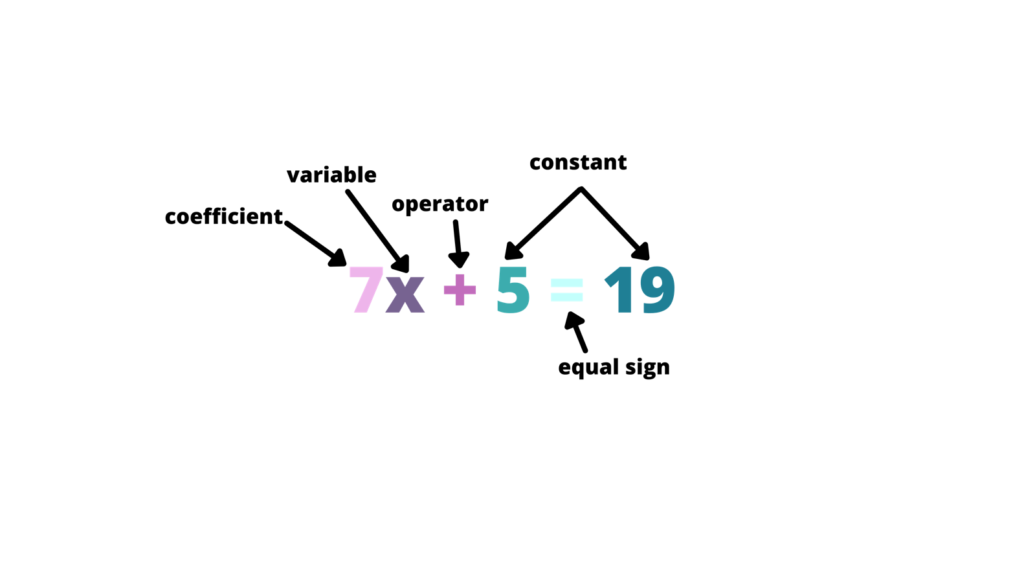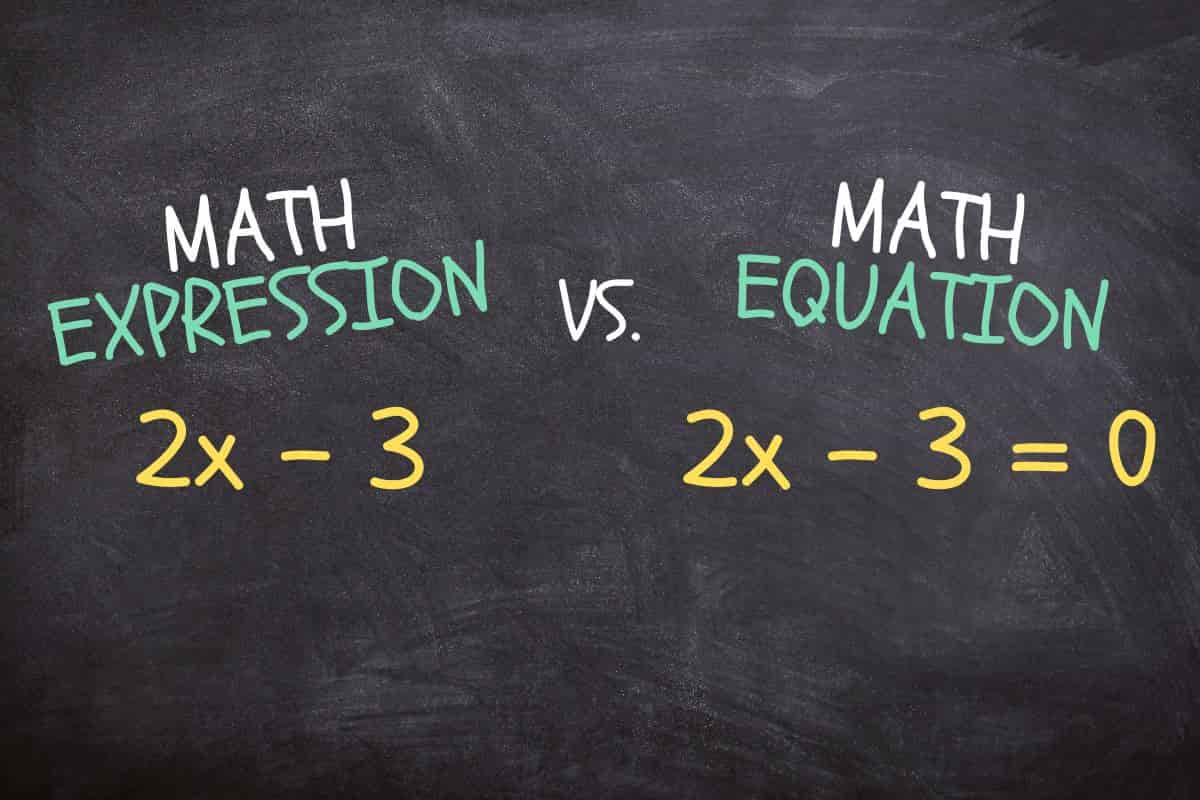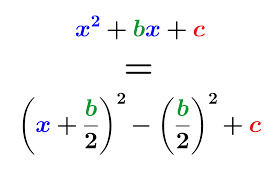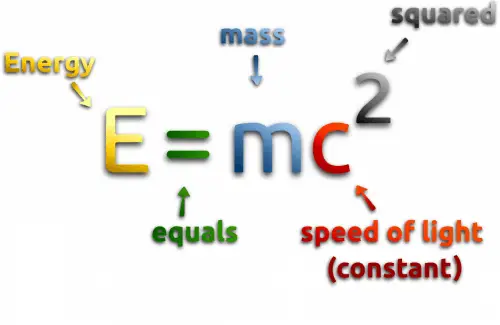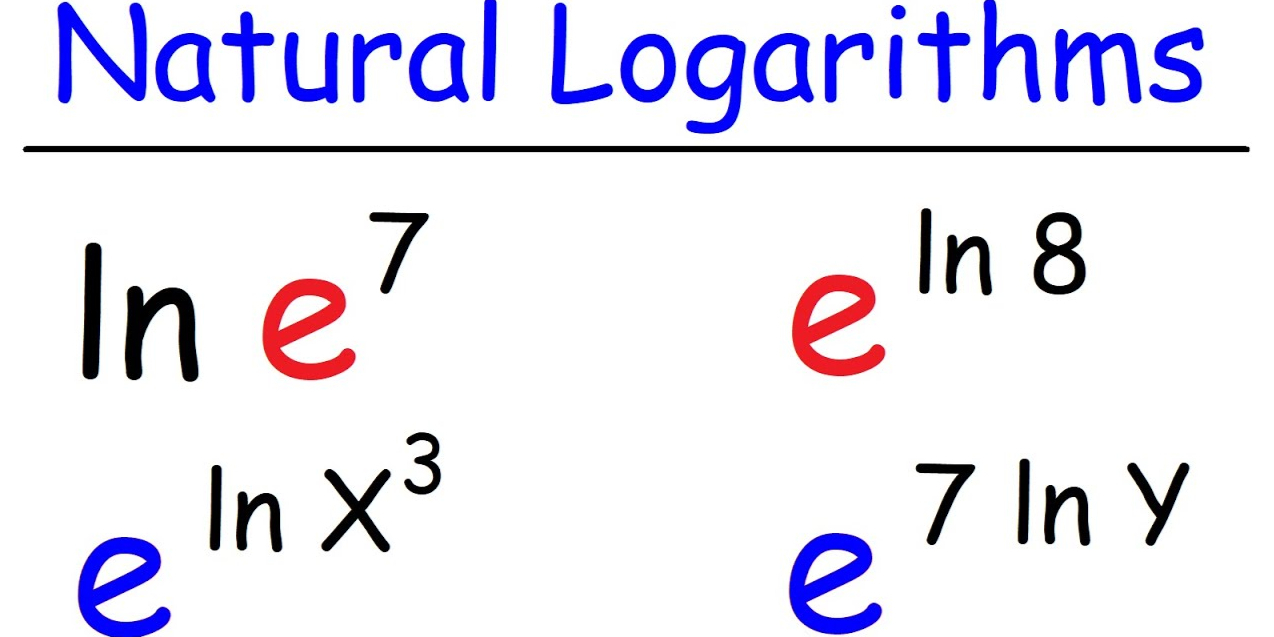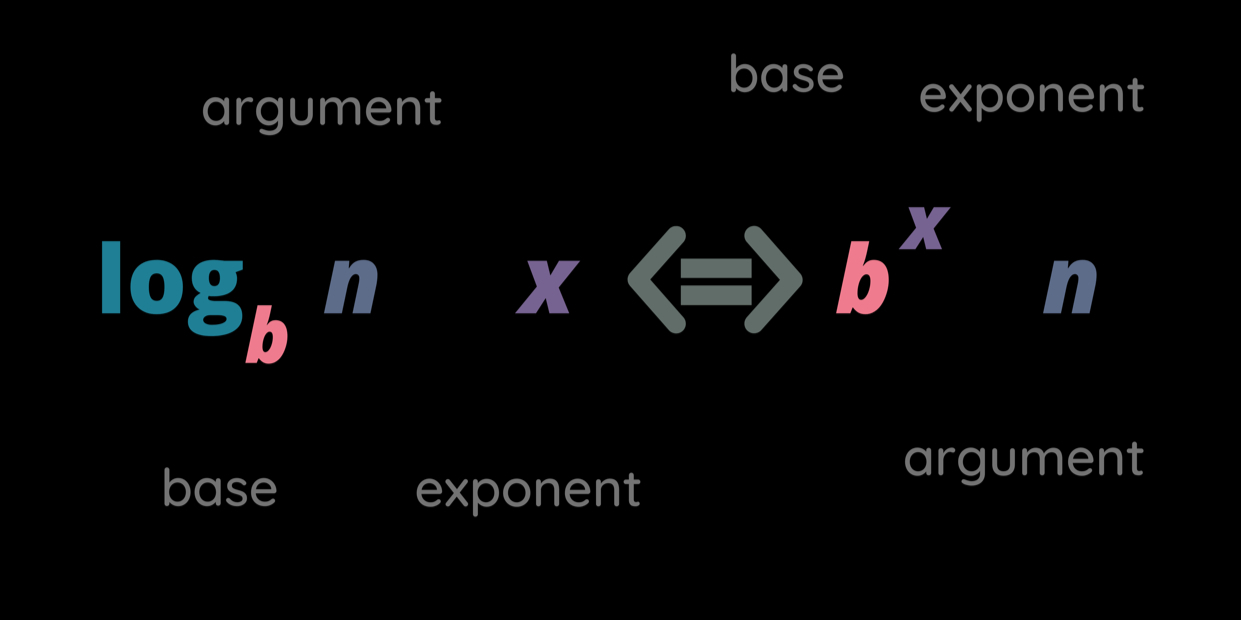What is an Equation?

Imagine creating your exercise schedule as a straight line, where the amount of time spent running increases proportionate to the distance covered; similarly, imagine expecting sales revenue to steadily rise with product sold by your business. Lines represent both of these relationships with great clarity. Linear equations go beyond simply being mathematical abstractions: they help analyze data, predict trends, and overcome daily challenges. Simply put, linear equations represent algebraically the straight-line relationship between two variables. Understanding how to find its mathematical representation in any situation--calculating mileage, creating budgets, or reading graphs -is vitally important. We will look at various techniques, principles, and practical applications of linear equations to achieve an answer in every possible context. In this article, we'll investigate these methods to arrive at and use linear equations efficiently in various applications.

Basic Concept of Equations

Definition of an Equation

An equation is a mathematical expression that states two quantities or expressions are equal. These can include terms, constants, coefficients, or even unknown values represented as variables. Equations utilize an "equal sign" (=) to connect expressions. For instance, when 2x+3=11 shows how when we calculate the left side, it equals 11 on the right. Mathematically, an equation may include algebraic expressions with equal operators, such as 2x = 8, as well as quadratic equations like \(x^{2} −3x+2=0\)

Mathematical Expression vs. Equation

Mathematical expressions and equations may look similar, but their functions and meanings are completely different. An expression is an arbitrary mathematical combination of numbers, operators, and variables (e.g. 2x + 3), while an equation uses an equal sign to balance the two expressions (for example, "2x+3 = 11" is an equation and "2x+3" is just an expression until it is further defined). Equation enables us to solve the problem of an unknown quantity, and it is a key tool in mathematics and other interdisciplinary fields.

Types of Equations

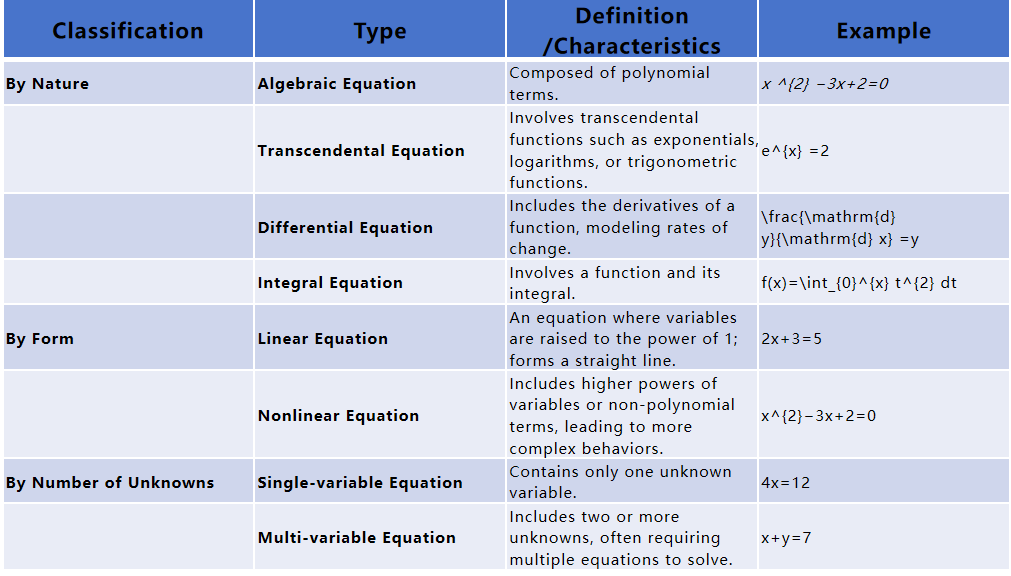
By Nature of the Equation

Algebraic equations like \(x^{2}−3x+2=0\) form the basis for problem-solving. Transcendental equations include exponential \(e^{x} =2\), logarithmic or trigonometric functions. Differential equations demonstrate changes over time using derivatives like \(\frac{\mathrm{d} y}{\mathrm{d} x} =y\), while integrals add depth in terms of analysis and application. Both types possess distinct methods for solving specific issues related to solving given problems.

By Form of the Equation

Equations can also be organized based on their structural form. Linear equations such as 2x + 3 = 5, in which variables are raised up to at most the first power, produce straight-line graphs, while nonlinear ones like \(x ^{2} −3x+2=0\) include terms with powers greater than one that produces more complex behaviors than straight line graphs.

By Number of Unknowns 

Equations vary based on their number of unknowns. Single-variable equations like 4x = 12 have only one unknown to solve for, while multi-variable ones like x+y=7 require solving two or more unknowns and may necessitate additional equations to reach unique solutions. Systems of equations usually employ substitution or elimination methods to reach simultaneous solutions.

Methods for Solving Equations

Basic Techniques

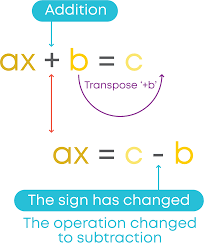
The transposition method

Transposition method of solving equations involves moving terms from one side of an equation to the other side to isolate an unknown variable. For instance, 2x + 3 = 11 we could transpose +3 onto other side and divide by 2, leading us to 4 as an answer for variable x. It works especially effectively when solving simple linear equations.

The factoring method

Factoring has become an increasingly popular method for solving quadratic equations, consisting of writing an expression as the sum of simpler terms with their zero-product property applied. For instance, solving \(x^{2}−x−6=0\) could involve factoring it as follows:(x - 3)(x + 2) = 0. When set equal to zero, this would become a solution: either x = 3 or -2, which are possible solutions.

Completing the square method

Completing the square is another technique for solving quadratic equations that rewrites them as perfect square trinomials, for instance, \(x^{2}+4x−5=0\). We would rewrite it as \((x+2)^{2}=9\), then take the square root and solve for x=−2±3, leading to x = 1 or x = -5. This technique is especially effective when the quadratic equation cannot be easily factorized.

Using calculators and software

Calculators and software provide efficient ways of solving both simple and complex equations in modern mathematics. An equation calculator is capable of directly solving quadratic equations while software such as MATLAB or Python excels at handling systems of multi-variable equations or performing numerical approximations methods to find solutions; entering an equation such as \(x^{2}+4x−5=0\) will often return answers like 1 and -5.

Advanced Techniques

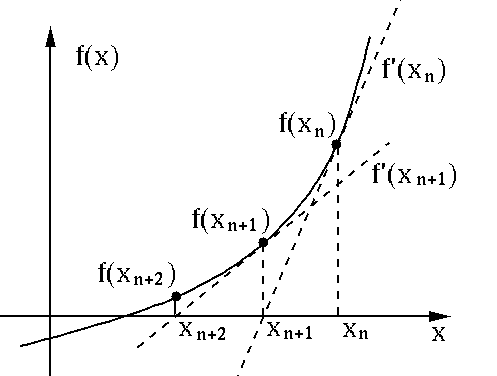
Advanced equations like transcendental or multi-variable systems typically require more sophisticated mathematical techniques for their solution. Numerical methods, like Newton Raphson methods, estimate approximate solutions iteratively when analytical solutions are infeasible (for instance, solving \(e^{x} =2\) yields an approximate value for x of 0.6993). Linear algebra techniques like Gaussian elimination or matrix inversion may also be applied systematically when it comes to multi-variable systems like \(2x+y=5\) and \(3x-y= 4\) can be expressed into matrix form for a systematic solution and then solved systematically using Gaussian elimination or matrix inversion - essential skills that make higher level mathematics work applications as well.

Applications of Equations

Historical Background

Studies of equations date back thousands of years. Ancient Babylonians used geometric solutions to solve linear and quadratic equations as early as 2000 BCE. The Persian mathematician Al-Khwarizmi made significant advancements in systematic solution of linear and quadratic equations in his book "Al-Kitab al-Mukhtasar fi Hisab al-Jabr wal-Muqabala" for this. By the 17th Century, René Descartes introduced Cartesian coordinates linking equations to geometric representation of geometric representation which revolutionized mathematics further than before.

Real-World Applications

Equations play an indispensable part in everyday life and scientific endeavors, from finance and engineering design to scientific investigation and investigation. Finance relies heavily on equations to model investments, loan repayments, and budget strategies; engineers employ differential algebra-derived differential equations when designing bridges, electrical circuits, or aerodynamic designs, while physics uses Newton's Second Law of Motion (\(F = ma\)) or Einstein's Energy Equation (\(E=mc^{2}\)) when explaining natural phenomena (such as planet predictions to developing AI algorithms!) Equations provide invaluable solutions across fields and professions!

Important Considerations for Mathematical Equations

Mathematical equations follow specific rules and characteristics that allow them to be easily comprehended and solved successfully.

Solutions or Roots of an Equation

The solution or root of an equation is a value that satisfies the equation. When a value replaces a variable in an equation to make both sides of the equation equal, this value is the root. For example, in the equation 2x+3 = 7, x = 2 is the solution because after substitution, 2×2+3 = 7, which verifies the correctness of the equation.

Maintaining Balance in the Equation

Subtracting, adding, multiplying, or dividing an equal number on both sides does not alter its solutions, upholding equality by isolating one variable at a time. For instance, subtraction five changed both sides to 3x = 15 before division by three led to 5 = 5, thus preserving equality throughout.

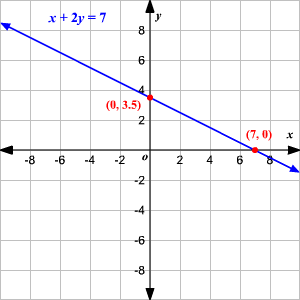
Graph of a Linear Equation

Linear equations involve variables raised only once to the power of 1, and its graph shows a constant rate of change between dependent and independent variables. For example, y = 2x + 1 is represented graphically as a straight line with a slope of two and an intercept at 1, as in its graph, demonstrating their linear relationship.

Verifying the Correctness of a Solution

Verifying that a solution is correct requires substituting its value back into its original equation if both sides remain equal, such as \(x^{2}−4=0\) in which solving gives 2 or -2, thus verifying its correctness by substituting either value into it (substituting either into it confirms its correctness).

In a word, equations are far more than just mathematical tools—they are the language of problem-solving in countless real-life scenarios. From managing personal budgets and designing engineering marvels to decoding the mysteries of the universe, equations empower us to make sense of the world around us. By understanding their definitions, types, and solutions, we can unlock their full potential to solve both simple and complex challenges. Whether you’re a student, a professional, or just curious about mathematics, mastering equations opens the door to endless possibilities in both everyday life and advanced scientific exploration. So, take the next step and start applying these concepts to the problems you encounter—equations might just be the key to your solutions!

Reference:

https://explorable.com/ancient-mathematics

https://www.wired.com/2014/10/invention-equals-sign/

https://www.investopedia.com/terms/m/montecarlosimulation.asp