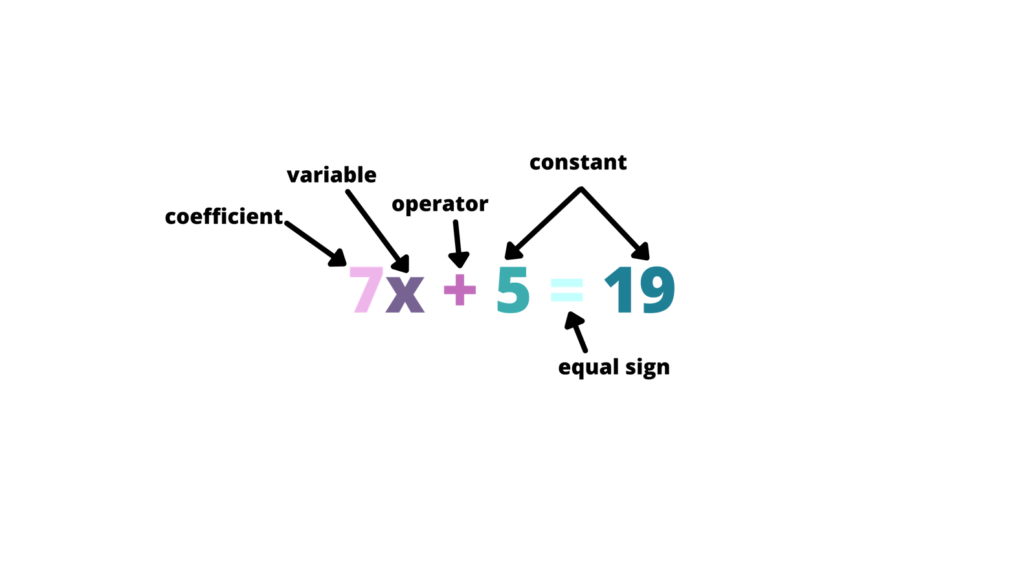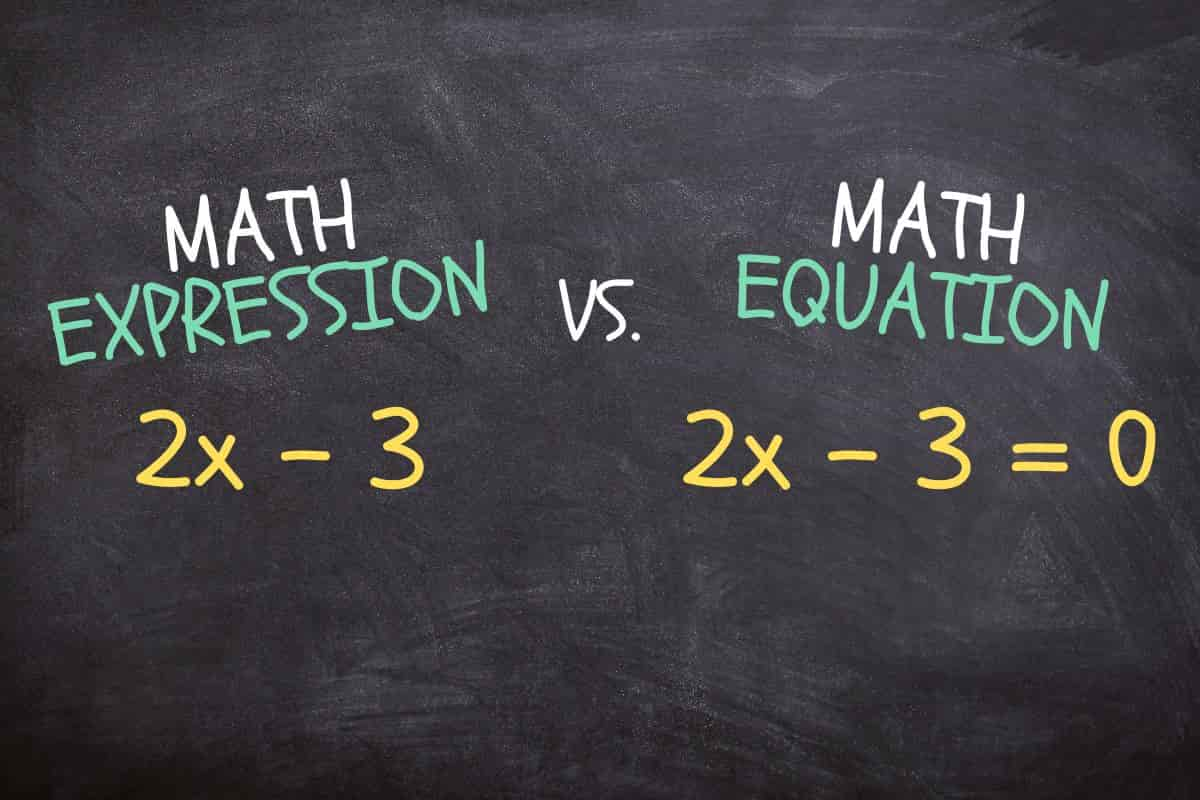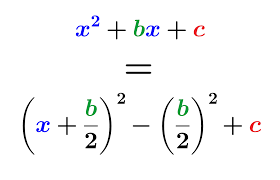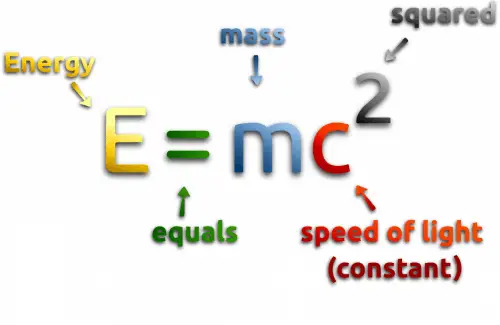¿Qué es una ecuación?

Imagina crear tu horario de ejercicios como una línea recta, donde la cantidad de tiempo dedicada a correr aumenta proporcionalmente a la distancia cubierta; de manera similar, imagina esperar que los ingresos por ventas aumenten de manera constante con los productos vendidos por tu negocio. Las líneas representan ambas relaciones con gran claridad. Las ecuaciones lineales van más allá de ser simples abstracciones matemáticas: ayudan a analizar datos, predecir tendencias y superar desafíos diarios. En pocas palabras, las ecuaciones lineales representan algebraicamente la relación de línea recta entre dos variables. Comprender cómo encontrar su representación matemática en cualquier situación—calcular kilometraje, crear presupuestos o leer gráficos—es de vital importancia. Observaremos diversas técnicas, principios y aplicaciones prácticas de las ecuaciones lineales para lograr una respuesta en cualquier contexto posible. En este artículo, investigaremos estos métodos para llegar a utilizar eficientemente las ecuaciones lineales en varias aplicaciones.

Concepto Básico de Ecuaciones

Definición de una Ecuación

Una ecuación es una expresión matemática que establece que dos cantidades o expresiones son iguales. Estas pueden incluir términos, constantes, coeficientes o incluso valores desconocidos representados como variables. Las ecuaciones utilizan un "signo igual" (=) para conectar expresiones. Por ejemplo, cuando 2x+3=11 muestra cómo al calcular el lado izquierdo, se iguala a 11 en el derecho. Matemáticamente, una ecuación puede incluir expresiones algebraicas con operadores de igualdad, como 2x = 8, así como ecuaciones cuadráticas como \(x^{2} −3x+2=0\)

Expresión Matemática vs. Ecuación

Las expresiones matemáticas y las ecuaciones pueden parecer similares, pero sus funciones y significados son completamente diferentes. Una expresión es una combinación matemática arbitraria de números, operadores y variables (e.g. 2x + 3), mientras que una ecuación utiliza un signo igual para equilibrar las dos expresiones (por ejemplo, "2x+3 = 11" es una ecuación y "2x+3" es solo una expresión hasta que se defina más). La ecuación nos permite resolver el problema de una cantidad desconocida, y es una herramienta fundamental en matemáticas y otros campos interdisciplinarios.

Tipos de Ecuaciones

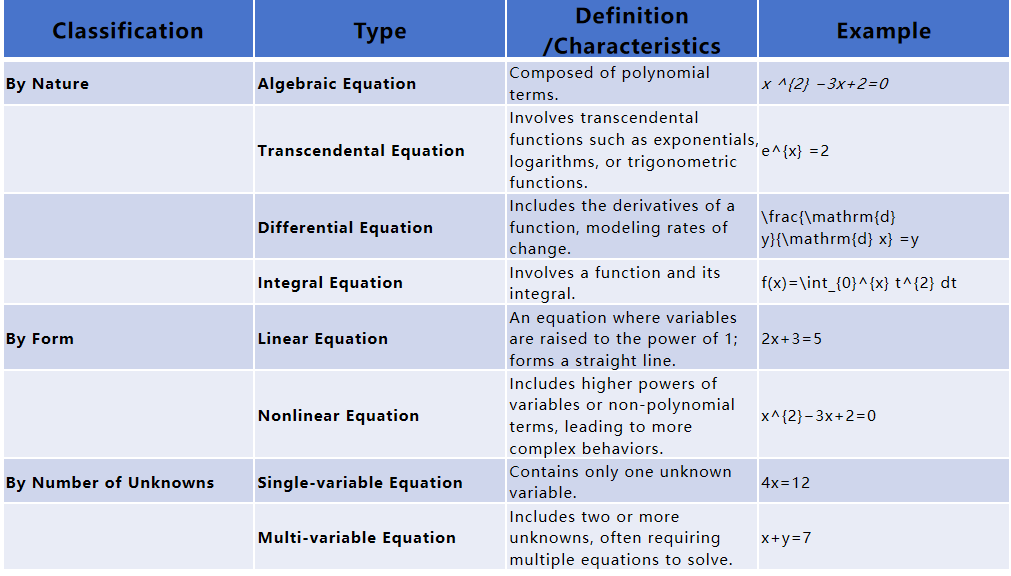
Por Naturaleza de la Ecuación

Las ecuaciones algebraicas como \(x^{2}−3x+2=0\) forman la base para la resolución de problemas. Las ecuaciones trascendentales incluyen funciones exponenciales \(e^{x} =2\), logarítmicas o trigonométricas. Las ecuaciones diferenciales demuestran cambios a lo largo del tiempo utilizando derivadas como \(\frac{\mathrm{d} y}{\mathrm{d} x} =y\), mientras que las integrales añaden profundidad en términos de análisis y aplicación. Ambos tipos poseen métodos distintos para resolver problemas específicos relacionados con la solución de problemas dados.

Por Forma de la Ecuación

Las ecuaciones también pueden organizarse en función de su forma estructural. Las ecuaciones lineales como 2x + 3 = 5, en las cuales las variables se elevan como máximo a la primera potencia, producen gráficos de línea recta, mientras que las no lineales como \(x ^{2} −3x+2=0\) incluyen términos con potencias superiores a uno que producen comportamientos más complejos que los gráficos de línea recta.

Por Número de Incógnitas 

Las ecuaciones varían según su número de incógnitas. Las ecuaciones de una sola variable como 4x = 12 tienen solo una incógnita a resolver, mientras que las de múltiples variables como x+y=7 requieren resolver dos o más incógnitas y pueden necesitar ecuaciones adicionales para alcanzar soluciones únicas. Los sistemas de ecuaciones suelen emplear métodos de sustitución o eliminación para alcanzar soluciones simultáneas.

Métodos para Resolver Ecuaciones

Técnicas Básicas

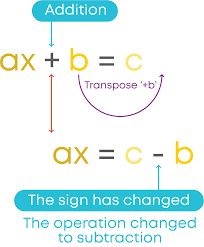
El método de transposición

El método de transposición para resolver ecuaciones implica mover términos de un lado de una ecuación al otro para aislar una variable desconocida. Por ejemplo, en 2x + 3 = 11 podríamos transponer +3 al otro lado y dividir por 2, lo que nos lleva a 4 como respuesta para la variable x. Funciona especialmente bien al resolver ecuaciones lineales simples.

El método de factorización

La factorización se ha vuelto un método cada vez más popular para resolver ecuaciones cuadráticas, que consiste en escribir una expresión como la suma de términos más simples con su propiedad de producto cero aplicada. Por ejemplo, resolver \(x^{2}−x−6=0\) podría implicar factorizarlo así: (x - 3)(x + 2) = 0. Al igualarlo a cero, esto se convertiría en una solución: x = 3 o -2, que son soluciones posibles.

El método de completar el cuadrado

Completar el cuadrado es otra técnica para resolver ecuaciones cuadráticas que las reescribe como trinomios de cuadrado perfecto, por ejemplo, \(x^{2}+4x−5=0\). Lo reescribiríamos como \((x+2)^{2}=9\), luego tomar la raíz cuadrada y resolver para x=−2±3, llevando a x = 1 o x = -5. Esta técnica es especialmente efectiva cuando la ecuación cuadrática no puede factorizarse fácilmente.

Usando calculadoras y software

Las calculadoras y el software proporcionan formas eficientes de resolver ecuaciones simples y complejas en las matemáticas modernas. Una calculadora de ecuaciones es capaz de resolver directamente ecuaciones cuadráticas mientras que software como MATLAB o Python sobresale al manejar sistemas de ecuaciones multivariables o realizar métodos de aproximaciones numéricas para encontrar soluciones; ingresar una ecuación como \(x^{2}+4x−5=0\) generalmente devuelve respuestas como 1 y -5.

Técnicas Avanzadas

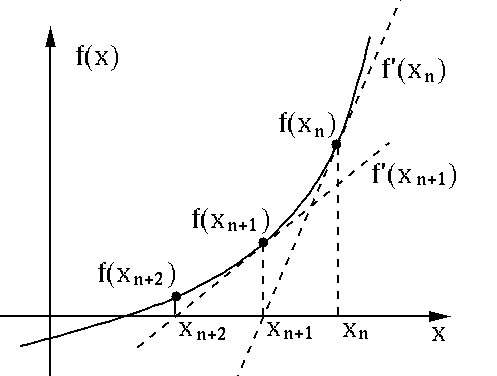
Ecuaciones avanzadas como los sistemas transcendentales o multivariables generalmente requieren técnicas matemáticas más sofisticadas para su solución. Métodos numéricos como los métodos de Newton Raphson estiman soluciones aproximadas iterativamente cuando las soluciones analíticas no son factibles (por ejemplo, resolver \(e^{x} =2\) arroja un valor aproximado para x de 0,6993). Técnicas de álgebra lineal como la eliminación gaussiana o la inversión de matrices también pueden aplicarse sistemáticamente cuando se trata de sistemas multivariables como \(2x+y=5\) y \(3x-y=4\) pueden expresarse en forma de matriz para una solución sistemática y luego resolverse sistemáticamente usando eliminación gaussiana o inversión de matrices - habilidades esenciales que hacen que el trabajo en matemáticas de nivel superior sea aplicable también.

Aplicaciones de las Ecuaciones

Antecedentes Históricos

Los estudios sobre ecuaciones se remontan a miles de años. Los antiguos babilonios utilizaban soluciones geométricas para resolver ecuaciones lineales y cuadráticas ya en el año 2000 a.C. El matemático persa Al-Juarismi realizó avances significativos en la solución sistemática de ecuaciones lineales y cuadráticas en su libro "Al-Kitab al-Mukhtasar fi Hisab al-Jabr wal-Muqabala". Para el siglo XVII, René Descartes introdujo las coordenadas cartesianas vinculando las ecuaciones a la representación geométrica, lo cual revolucionó las matemáticas más allá de lo que se había logrado anteriormente.

Aplicaciones en el Mundo Real

Las ecuaciones juegan un papel indispensable en la vida cotidiana y en los esfuerzos científicos, desde las finanzas y el diseño de ingeniería hasta la investigación científica. Las finanzas dependen en gran medida de las ecuaciones para modelar inversiones, reembolsos de préstamos y estrategias presupuestarias; los ingenieros emplean ecuaciones diferenciales derivadas del álgebra al diseñar puentes, circuitos eléctricos o diseños aerodinámicos; mientras que la física utiliza la Segunda Ley del Movimiento de Newton (\(F = ma\)) o la Ecuación de la Energía de Einstein (\(E=mc^{2}\)) para explicar fenómenos naturales (¡desde predicciones planetarias hasta el desarrollo de algoritmos de IA!) ¡Las ecuaciones proporcionan soluciones invaluables en diversos campos y profesiones!

Consideraciones Importantes para las Ecuaciones Matemáticas

Las ecuaciones matemáticas siguen reglas y características específicas que permiten que sean fácilmente comprendidas y resueltas con éxito.

Soluciones o Raíces de una Ecuación

La solución o raíz de una ecuación es un valor que satisface la ecuación. Cuando un valor reemplaza una variable en una ecuación para que ambos lados sean iguales, este valor es la raíz. Por ejemplo, en la ecuación 2x+3 = 7, x = 2 es la solución porque después de la sustitución, 2×2+3 = 7, lo que verifica la corrección de la ecuación.

Mantener el Equilibrio en la Ecuación

Restar, sumar, multiplicar o dividir un número igual en ambos lados no altera sus soluciones, manteniendo la igualdad al aislar una variable a la vez. Por ejemplo, restar cinco cambió ambos lados a 3x = 15 antes de la división por tres, lo que llevó a 5 = 5, preservando así la igualdad en todo momento.

Gráfico de una Ecuación Lineal

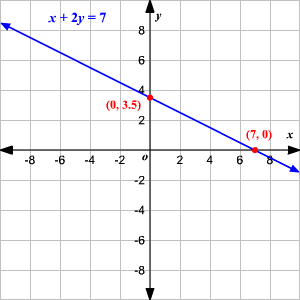
Las ecuaciones lineales involucran variables elevadas solo una vez a la potencia de 1, y su gráfico muestra una tasa de cambio constante entre las variables dependientes e independientes. Por ejemplo, y = 2x + 1 se representa gráficamente como una línea recta con una pendiente de dos y una intersección en 1, como en su gráfico, demostrando su relación lineal.

Verificando la Corrección de una Solución

Verificar que una solución es correcta requiere sustituir su valor de nuevo en su ecuación original; si ambos lados permanecen iguales, como \(x^{2}−4=0\) en la cual la solución es 2 o -2, verificando así su corrección al sustituir cualquiera de los valores en ella (sustituir cualquiera de ellos confirma su corrección).

En resumen, las ecuaciones son mucho más que simples herramientas matemáticas: son el lenguaje de la resolución de problemas en innumerables escenarios de la vida real. Desde gestionar presupuestos personales y diseñar maravillas de la ingeniería hasta descifrar los misterios del universo, las ecuaciones nos permiten entender el mundo que nos rodea. Al comprender sus definiciones, tipos y soluciones, podemos desbloquear su completo potencial para resolver tanto desafíos simples como complejos. Ya seas un estudiante, un profesional, o simplemente alguien curioso por las matemáticas, dominar las ecuaciones abre la puerta a infinitas posibilidades tanto en la vida cotidiana como en la exploración científica avanzada. Así que, da el siguiente paso y comienza a aplicar estos conceptos a los problemas que enfrentas: ¡las ecuaciones podrían ser la clave de tus soluciones!

Referencia:

https://explorable.com/ancient-mathematics

https://www.wired.com/2014/10/invention-equals-sign/

https://www.investopedia.com/terms/m/montecarlosimulation.asp