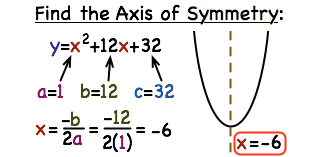What is the Equation of Axis of Symmetry?

Understanding the Axis of Symmetry

Definition of the Axis of Symmetry

An axis of symmetry is an integral concept in geometry and algebra, serving as an imaginary line dividing mathematical figures, objects, or equations into equal and mirror-image halves. Each point on either side of this imaginary axis corresponds with another on either side and lies equidistant from it - providing perfect symmetry and equilibrium and making this line essential when studying shapes or their properties.

Physically speaking, symmetry can be found everywhere: butterfly wings that split along their bodies are an example of this; similarly, curved river banks reflected by monumental works such as the Taj Mahal also exhibit this quality in their artistic designs.

From a mathematical viewpoint, understanding various functions and shapes requires understanding the axis of symmetry. For example, quadratic equations utilize it as an element that divides parabolas into identical halves with its vertex on it - providing us with a tool for finding solutions, graphing equations, or comprehending real-world issues modeled with parabolas.

Different Orientations of the Axis of Symmetry

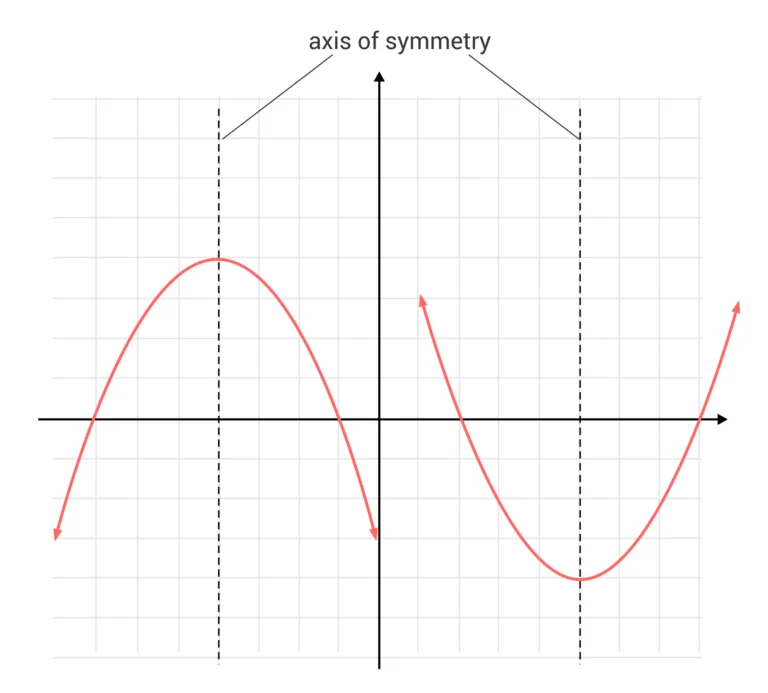
The orientation of an axis depends on what shape or equation is under analysis. In two-dimensional geometry, these can either be horizontal, vertical, or diagonal, depending on their alignment and positioning.

Horizontal and Vertical Axes in Parabolas

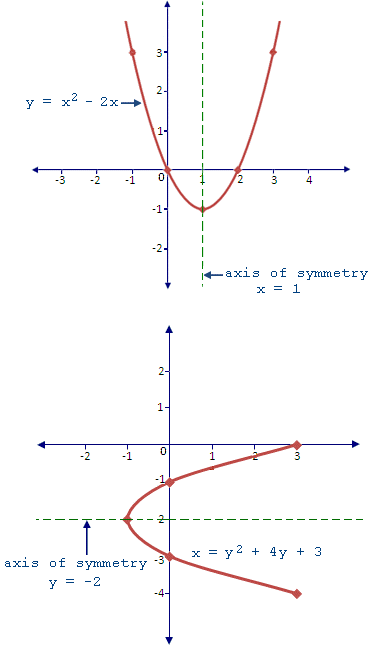
A vertical axis of symmetry is most commonly associated with parabolas that open upward or downward. This axis intersects the vertex and serves as a line of division, denoted as x = constant.

A horizontal axis of symmetry occurs in parabolas that open left or right. In this case, the division line is written as y = constant.

For example, consider parabolas represented by the equations \(y = 4x^{2} - 8x + 3\) (opening vertically) and\(x = -2y^{2} + 6y - 1\) (opening horizontally). The axis of symmetry for the former is a vertical line, while for the latter, it is horizontal. These distinctions are significant when solving or graphing quadratic equations.

Beyond Two Dimensions: Symmetry in 3D Shapes

While the understanding of symmetry often centers on two-dimensional phenomena, it expands into three-dimensional shapes as well. Symmetry in 3D space has far-reaching applications in geometry, architecture, physics, and even molecular biology.

Consider a sphere, which has infinitely many axes of symmetry passing through its center, or a circle, which can rotate around any axis perpendicular to the plane without changing its appearance. Likewise, cylinders and cones demonstrate unique symmetric properties. For instance, a cone's cone's rotational symmetry around its vertical axis ensures that its circular base remains consistent regardless of the angle of view. Understanding these instances emphasizes how symmetry transcends dimensions and contributes valuable insights, from visualizing atomic structures to analyzing engineering designs.

The Axis of Symmetry in Parabolas

Characteristics of the Parabola's Axis of Symmetry

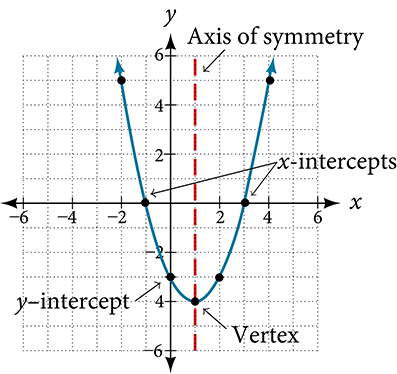
The parabola is a prominent example where the axis of symmetry plays a vital role. Defined as the curve created by a quadratic equation, a parabola is inherently symmetrical. Its axis of symmetry passes through its vertex, dividing it into two identical halves. This axis is fundamental in determining the shape, orientation, and many algebraic properties of the parabola.

How the Shape Relates to Symmetry

The parabola's vertex lies at the point where the axis of symmetry crosses it, identifying the highest or lowest point depending on the parabola's orientation. Whether the parabola opens upwards (e.g., \(y = x^{2}\)) or downward (\(y = -x^{2}\) ), the axis is the vertical line x-coordinate of the vertex. For equations where the parabola opens horizontally, such as in x = y^{2}, the axis of symmetry becomes a horizontal line where the vertex is located.

For example, take the quadratic equation \(y = x^{2} - 4x + 4\) . Rearranging the equation leads you to see the vertex is at x = 2, meaning the axis of symmetry is x = 2. This understanding can significantly simplify the process of solving or graphing the equation, enabling a more precise visualization of the curve.

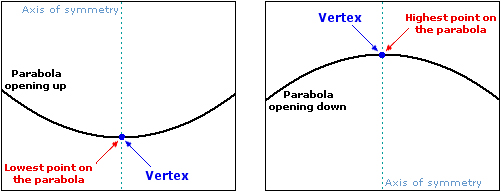
Vertex as the Keystone of the Axis of Symmetry

A parabola's vertex serves as its centerpiece of symmetry. Mathematically speaking, this singular point represents where its axis of symmetry intersects it; depending on its orientation, it could represent either its maximum or minimum point.

The importance of the vertex extends beyond geometry into practical applications. Algebraically, the vertex is often used to locate the axis of symmetry quickly, particularly when the equation is written in vertex form (\(y = a(x-h)^{2} + k\)), where x = h directly determines the axis of symmetry.

Applications of Vertex in Real-World Problem-Solving

Vertex-based symmetry has an inextricable link to real-world issues. Parabolas in physics are used to represent projectile motion; when launched into the air from a launch pad, it forms an ellipsis with its center passing through its maximum height (the vertex). Furthermore, economics makes use of vertex equations in which their vertex represents the price point that maximizes profit, an invaluable concept when making business decisions.

Parabolic arches used on bridges or aqueducts rely on the principles of the axis of symmetry to distribute weight evenly, making these design structures not only visually appealing but structurally sound as well.

Focusing on the vertex as its pivot point, symmetry principles become an invaluable analytical tool that is applicable across disciplines.

Equations of the Axis of Symmetry

Formula for a Standard Quadratic Equation

Quadratic equations are often expressed in their standard form :

\(y = ax^{2} + bx + c\)

Here, a, b , and c are constants where:

a determines the parabola's direction (opens upward or downward if positive or negative, respectively) and width.

b affects the position of the parabola relative to the y-axis.

c corresponds to the y-intercept, showing where the parabola crosses the y-axis.

The axis of symmetry for this form is derived using a simple yet powerful formula:

\(x = - \frac{b}{2a}\)

This equation allows us to calculate the x-coordinate of the vertex, effectively locating the axis of symmetry. For example, consider the quadratic equation \(y = 2x^{2} - 4x + 3\). Substituting a = 2 and b = -4 , we get:

\(x = -\frac{-4}{2\times2 } = 4 / 4 = 1\)

Thus, the axis of symmetry is x = 1, which means the parabola is symmetrical around this vertical line. You can try more exercise on question bank about equations.

Visualization Through Graphs

Graphing makes it easier to visualize how the axis of symmetry divides the parabola. For instance, if you plot \(y = x^{2} - 6x + 8\), you'll see the distinct vertical axis at x = 3, which passes through the vertex. Using graphing software like Desmos or tools such as a graphing calculator validates this visually. This method serves as an excellent way to engage with symmetry, reinforcing the algebraic concepts while adding a hands-on component.

Axis of Symmetry in Vertex Form

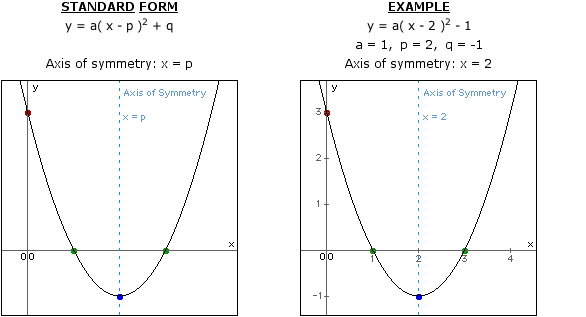
Another popular representation of quadratic equations is the vertex form, given by:

\(y = a(x-h)^{2} + k\)

Here, the vertex is defined as (h, k). By design, the axis of symmetry is directly related to the h value of the vertex, making it x = h in this form. This is particularly convenient for problems that provide equations already in vertex form or allow for easy conversion from standard form.

For example, the equation \(y = 2(x-3)^{2} + 5\) immediately indicates that the axis of symmetry is x = 3, as the formula centers the parabola around this value.

Axis of Symmetry Derivation Using General Equations

Sometimes, you may need to derive the axis of symmetry using more general methods or outside the context of standard forms.

Using Symmetrical Points to Derive Axis

Consider a situation where you know two points on a parabola that are symmetrical relative to the axis. For example, take the points (4, 7) and (0, 7). Their symmetry indicates that the axis lies midway between their x-coordinates. Using the midpoint formula:

x = (4 + 0) / 2 = 2

This derivation confirms the symmetry axis as x = 2, showcasing how geometric analysis can complement algebraic solutions.

Beyond Parabolas: Symmetry in Other Functions

While parabolas often dominate the discussion of symmetry, other shapes like ellipses and circles also rely heavily on symmetric properties. For example, a circle, defined by \((x-h)^{2} + (y-k)^{2} = (r)^{2}\), has infinite axes of symmetry passing through its center (h, k). Similarly, ellipses have both horizontal and vertical axes of symmetry, which is critical in calculus and physical applications like orbital mechanics.

Unique Methods to Identify the Axis of Symmetry

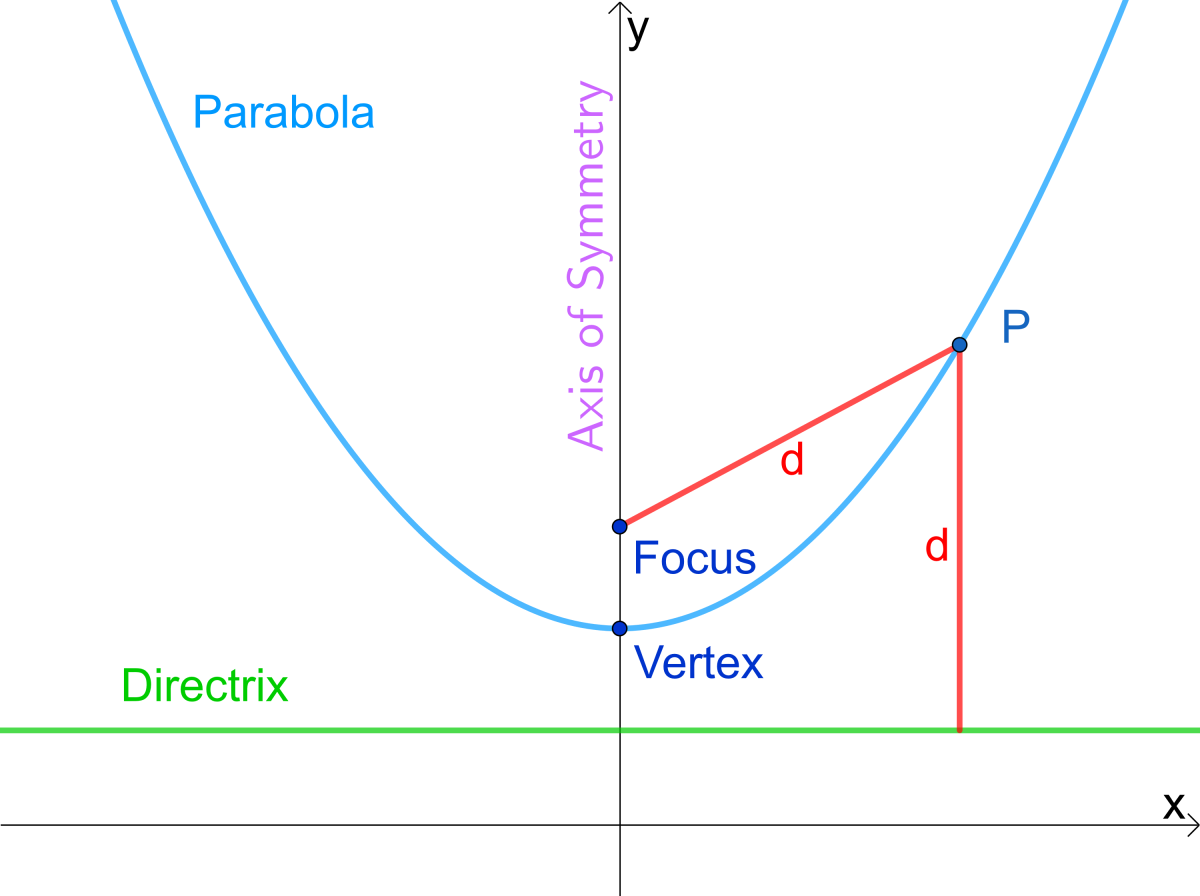
Using Directrix and Focus of a Parabola

As well as using equations to pinpoint its symmetry axis, directrix and focus can offer geometric insights for pinpointing it. They define its shape and orientation while its vertex lies midway. A perpendicular line from the vertex through focus is considered to be its axis of symmetry.

Symmetry Derived via Distance Properties

Parabolas can be easily distinguished from their peers due to one distinguishing property - maintaining equal distances from both focus and directrix points on its curves at any point on their paths. Utilizing this distance property, the step-by-step axis of symmetry derivation becomes possible, providing another approach in addition to algebraic methods for the derivation of such structures.

Conclusion

The axis of symmetry is a cornerstone concept in mathematics and geometry, dividing figures and equations into perfectly mirrored halves. Its equation, whether derived through \(x = - \frac{b}{2a}\) for standard quadratic forms or directly from the vertex, is a powerful tool for analyzing shapes, solving problems, and visualizing patterns.

Beyond mathematics, the axis of symmetry has practical applications in fields like physics, architecture, and engineering, underpinning designs that are not only functional but also visually harmonious. By mastering this concept, you gain insight into the elegance of symmetry and its impact on both theory and real-world applications, bridging the gap between calculation and creativity.

Reference:

https://insights.jonite.com/the-art-of-symmetry-in-architecture

https://mfaizan.github.io/2022/10/02/symmetry.html

https://shs.hal.science/halshs-03048686v1/file/20030.pdf