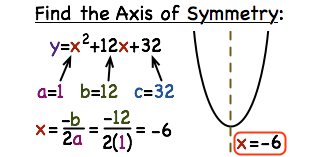¿Cuál es la ecuación del eje de simetría?

Entendiendo el Eje de Simetría

Definición del Eje de Simetría

Un eje de simetría es un concepto integral en geometría y álgebra, que sirve como una línea imaginaria que divide figuras matemáticas, objetos o ecuaciones en mitades iguales e imagen espejo. Cada punto a ambos lados de este eje imaginario corresponde con otro en el lado opuesto y está a la misma distancia de él, proporcionando perfecta simetría y equilibrio, y haciendo de esta línea un elemento esencial al estudiar las formas o sus propiedades.

Físicamente hablando, la simetría se encuentra en todas partes: las alas de las mariposas que se dividen a lo largo de sus cuerpos son un ejemplo de esto; de manera similar, las riveras curvas reflejadas por obras monumentales como el Taj Mahal también exhiben esta cualidad en sus diseños artísticos.

Desde un punto de vista matemático, entender distintas funciones y formas requiere entender el eje de simetría. Por ejemplo, las ecuaciones cuadráticas lo utilizan como un elemento que divide las parábolas en mitades idénticas con su vértice sobre él, proporcionándonos una herramienta para encontrar soluciones, graficar ecuaciones o comprender problemas del mundo real modelados con parábolas.

Diferentes Orientaciones del Eje de Simetría

La orientación de un eje depende de qué forma o ecuación está bajo análisis. En geometría bidimensional, estos pueden ser horizontales, verticales o diagonales, dependiendo de su alineación y posicionamiento.

Ejes Horizontales y Verticales en Parábolas

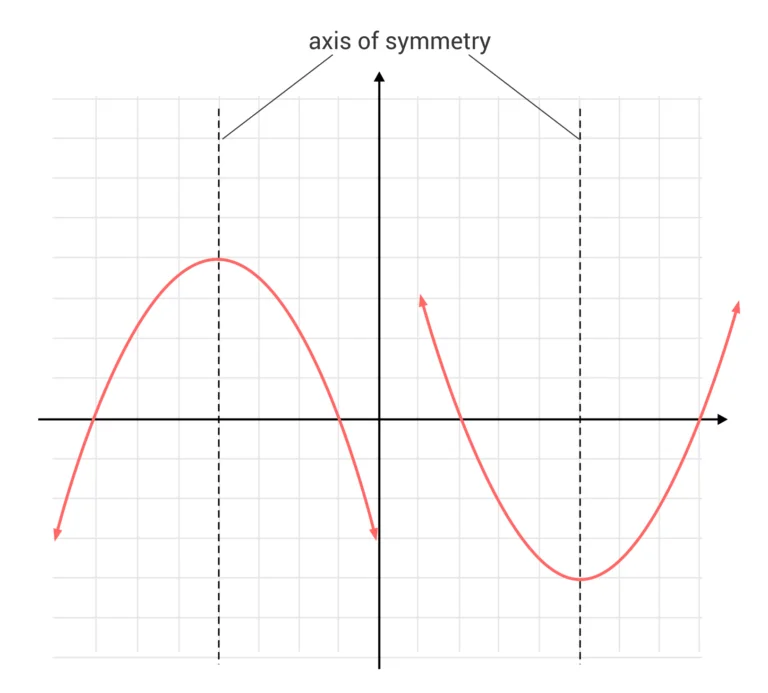
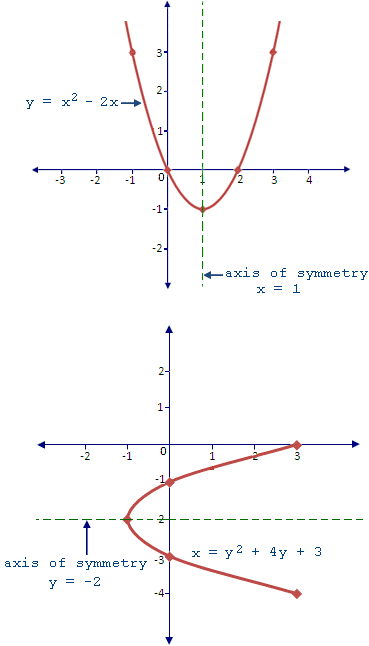
Un eje de simetría vertical se asocia más comúnmente con parábolas que se abren hacia arriba o hacia abajo. Este eje intersecta el vértice y sirve como línea de división, denotada como x = constante.

Un eje de simetría horizontal ocurre en parábolas que se abren a la izquierda o derecha. En este caso, la línea de división se escribe como y = constante.

Por ejemplo, considere parábolas representadas por las ecuaciones \(y = 4x^{2} - 8x + 3\) (abriendo verticalmente) y\(x = -2y^{2} + 6y - 1\) (abriendo horizontalmente). El eje de simetría para la primera es una línea vertical, mientras que para la segunda, es horizontal. Estas distinciones son significativas al resolver o graficar ecuaciones cuadráticas.

Más Allá de Dos Dimensiones: Simetría en Formas 3D

Aunque la comprensión de la simetría a menudo se centra en fenómenos bidimensionales, se extiende también a las formas tridimensionales. La simetría en el espacio 3D tiene aplicaciones de gran alcance en geometría, arquitectura, física e incluso biología molecular.

Considere una esfera, que tiene infinidad de ejes de simetría que pasan por su centro, o un círculo, que puede girar alrededor de cualquier eje perpendicular al plano sin cambiar su apariencia. Del mismo modo, cilindros y conos demuestran propiedades simétricas únicas. Por ejemplo, la simetría rotacional de un cono alrededor de su eje vertical asegura que su base circular se mantenga consistente sin importar el ángulo de vista. Entender estas instancias enfatiza cómo la simetría trasciende dimensiones y contribuye con valiosos conocimientos, desde visualizar estructuras atómicas hasta analizar diseños de ingeniería.

El eje de simetría en parabolas

Características del eje de simetría de la parábola

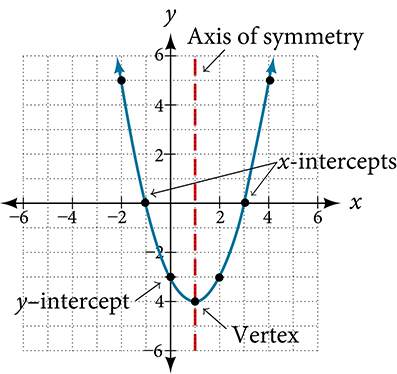
La parábola es un ejemplo destacado donde el eje de simetría desempeña un papel vital. Definida como la curva creada por una ecuación cuadrática, una parábola es inherentemente simétrica. Su eje de simetría pasa por su vértice, dividiéndola en dos mitades idénticas. Este eje es fundamental para determinar la forma, orientación y muchas propiedades algebraicas de la parábola.

Cómo se relaciona la forma con la simetría

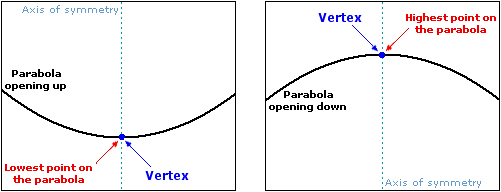
El vértice de la parábola se encuentra en el punto donde el eje de simetría la cruza, identificando el punto más alto o más bajo dependiendo de la orientación de la parábola. Ya sea que la parábola se abra hacia arriba (por ejemplo, \(y = x^{2}\)) o hacia abajo (\(y = -x^{2}\)), el eje es la línea vertical correspondiente a la coordenada x del vértice. Para ecuaciones donde la parábola se abre horizontalmente, como en x = y^{2}, el eje de simetría se convierte en una línea horizontal donde se encuentra el vértice.

Por ejemplo, tome la ecuación cuadrática \(y = x^{2} - 4x + 4\). Reorganizar la ecuación te lleva a ver que el vértice está en x = 2, lo que significa que el eje de simetría es x = 2. Esta comprensión puede simplificar significativamente el proceso de resolver o graficar la ecuación, permitiendo una visualización más precisa de la curva.

El vértice como la clave del eje de simetría

El vértice de una parábola sirve como su eje central de simetría. Desde una perspectiva matemática, este punto singular representa donde su eje de simetría la intersecta; dependiendo de su orientación, podría representar su punto máximo o mínimo.

La importancia del vértice se extiende más allá de la geometría hacia aplicaciones prácticas. Algebraicamente, el vértice se usa a menudo para ubicar rápidamente el eje de simetría, particularmente cuando la ecuación está escrita en forma de vértice (\(y = a(x-h)^{2} + k\)), donde x = h determina directamente el eje de simetría.

Aplicaciones del vértice en la resolución de problemas del mundo real

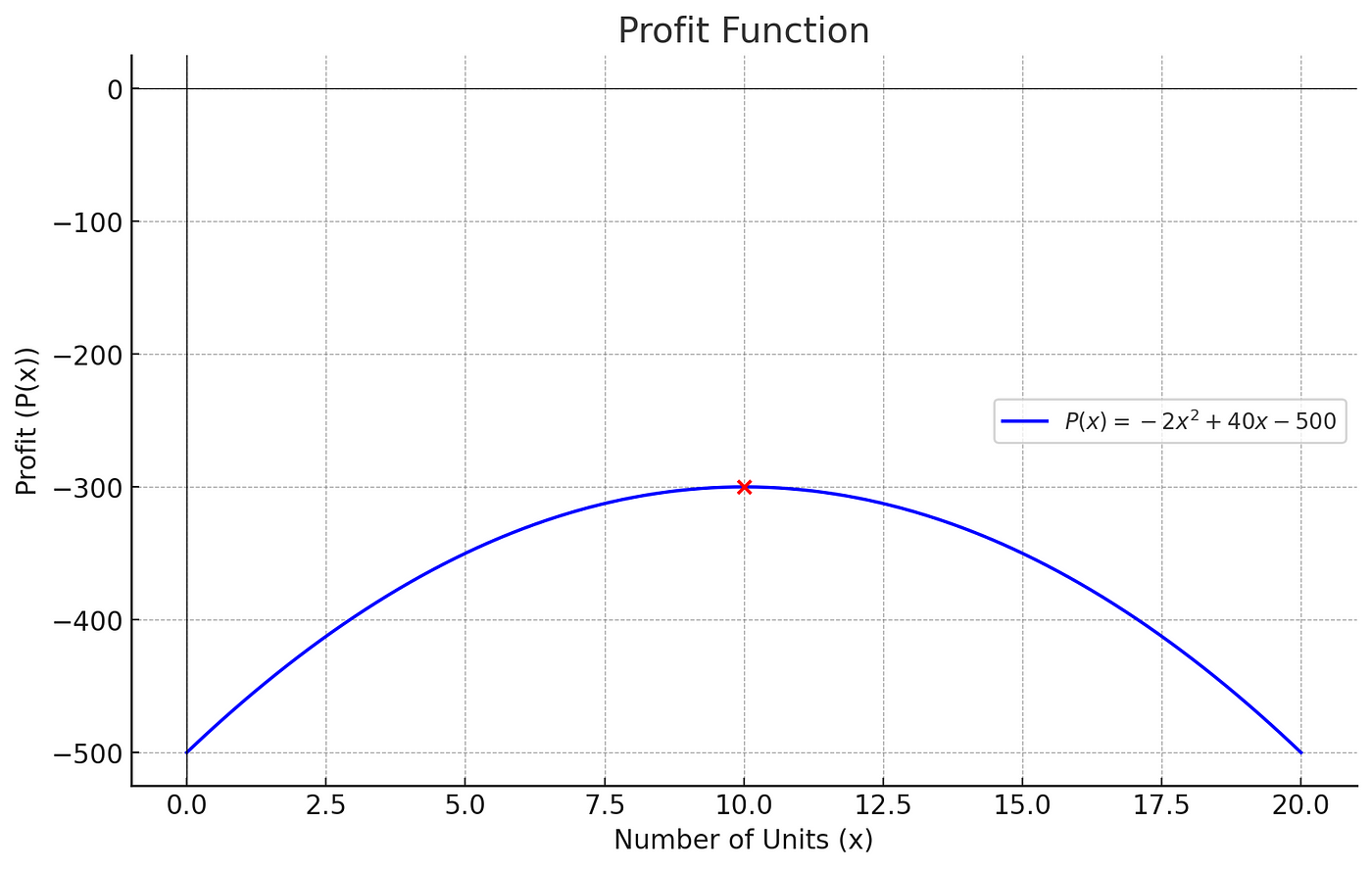
La simetría basada en el vértice tiene un vínculo inextricable con los problemas del mundo real. Las parábolas en física se utilizan para representar el movimiento de proyectiles; cuando se lanzan al aire desde una plataforma de lanzamiento, forman una elipse con su centro pasando por su altura máxima (el vértice). Además, la economía utiliza ecuaciones de vértice en las que su vértice representa el punto de precio que maximiza las ganancias, un concepto invaluable al tomar decisiones comerciales.

Los arcos parabólicos utilizados en puentes o acueductos se basan en los principios del eje de simetría para distribuir el peso de manera uniforme, haciendo que estas estructuras de diseño no solo sean atractivas visualmente sino también estructuralmente sólidas.

Enfocándose en el vértice como punto de pivote, los principios de simetría se convierten en una herramienta analítica invaluable aplicable en diversas disciplinas.

Ecuaciones del Eje de Simetría

Fórmula para una Ecuación Cuadrática Estándar

Las ecuaciones cuadráticas a menudo se expresan en su forma estándar:

\(y = ax^{2} + bx + c\)

Aquí, a, b y c son constantes donde:

a determina la dirección de la parábola (se abre hacia arriba o hacia abajo si es positivo o negativo, respectivamente) y el ancho.

b afecta la posición de la parábola con respecto al eje y.

c corresponde a la intersección con el eje y, mostrando dónde la parábola cruza el eje y.

El eje de simetría para esta forma se deriva utilizando una fórmula simple pero poderosa:

\(x = - \frac{b}{2a}\)

Esta ecuación nos permite calcular la coordenada x del vértice, ubicando efectivamente el eje de simetría. Por ejemplo, considere la ecuación cuadrática \(y = 2x^{2} - 4x + 3\). Sustituyendo a = 2 y b = -4, obtenemos:

\(x = -\frac{-4}{2\times2 } = 4 / 4 = 1\)

Por lo tanto, el eje de simetría es x = 1, lo que significa que la parábola es simétrica alrededor de esta línea vertical. Puedes intentar más ejercicios en banco de preguntas sobre ecuaciones.

Visualización a Través de Gráficos

Hacer gráficos facilita visualizar cómo el eje de simetría divide la parábola. Por ejemplo, si trazas \(y = x^{2} - 6x + 8\), verás el eje vertical distinto en x = 3, que pasa por el vértice. Usar software de gráficos como Desmos o herramientas como una calculadora gráfica valida esto visualmente. Este método sirve como una excelente manera de interactuar con la simetría, reforzando los conceptos algebraicos mientras se añade un componente práctico.

Eje de Simetría en Forma de Vértice

Otra representación popular de las ecuaciones cuadráticas es la forma de vértice, dada por:

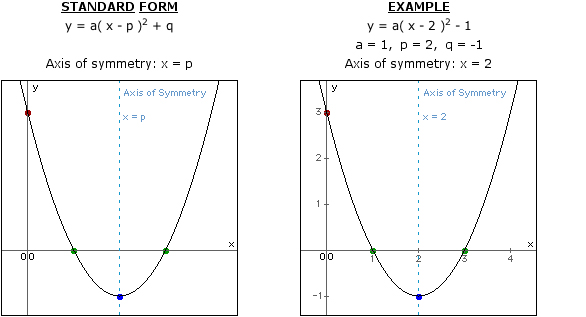
\(y = a(x-h)^{2} + k\)

Aquí, el vértice se define como (h, k). Por diseño, el eje de simetría está directamente relacionado con el valor h del vértice, lo que lo convierte en x = h en esta forma. Esto es especialmente conveniente para problemas que brindan ecuaciones ya en forma de vértice o permiten una fácil conversión desde la forma estándar.

Por ejemplo, la ecuación \(y = 2(x-3)^{2} + 5\) indica inmediatamente que el eje de simetría es x = 3, ya que la fórmula centra la parábola alrededor de este valor.

Derivación del Eje de Simetría Usando Ecuaciones Generales

A veces, puede que necesites derivar el eje de simetría usando métodos más generales o fuera del contexto de las formas estándar.

Uso de Puntos Simétricos para Derivar el Eje

Considera una situación donde conoces dos puntos en una parábola que son simétricos con respecto al eje. Por ejemplo, toma los puntos (4, 7) y (0, 7). Su simetría indica que el eje se encuentra a medio camino entre sus coordenadas x. Usando la fórmula del punto medio:

x = (4 + 0) / 2 = 2

Esta derivación confirma que el eje de simetría es x = 2, mostrando cómo el análisis geométrico puede complementar las soluciones algebraicas.

Más Allá de las Parábolas: Simetría en Otras Funciones

Aunque las parábolas a menudo dominan la discusión sobre simetría, otras formas como elipses y círculos también dependen mucho de propiedades simétricas. Por ejemplo, un círculo, definido por \((x-h)^{2} + (y-k)^{2} = (r)^{2}\), tiene infinitos ejes de simetría que pasan por su centro (h, k). De manera similar, las elipses tienen ejes de simetría horizontales y verticales, lo cual es crítico en cálculo y aplicaciones físicas como la mecánica orbital.

Métodos Únicos para Identificar el Eje de Simetría

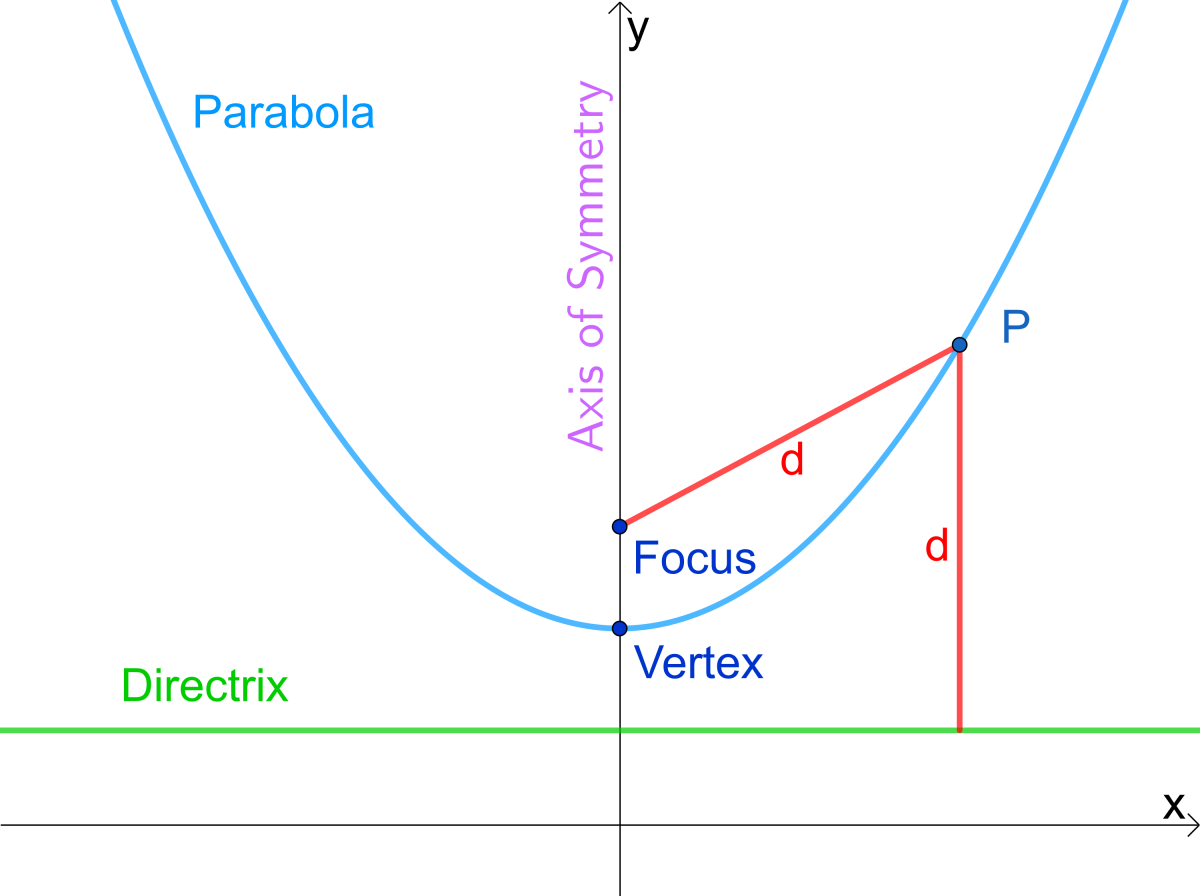
Usando la Directriz y el Foco de una Parábola

Además de usar ecuaciones para identificar su eje de simetría, la directriz y el foco pueden ofrecer perspectivas geométricas para localizarlo. Definen su forma y orientación mientras su vértice se encuentra en el punto medio. Una línea perpendicular desde el vértice a través del foco se considera su eje de simetría.

Simetría Derivada a través de Propiedades de Distancia

Las parábolas se pueden distinguir fácilmente de sus semejantes debido a una propiedad distintiva: mantener distancias iguales desde ambos puntos de foco y directriz en sus curvas en cualquier punto de sus trayectorias. Utilizando esta propiedad de distancia, se convierte en posible la derivación paso a paso del eje de simetría, proporcionando otro enfoque además de los métodos algebraicos para la derivación de tales estructuras.

Conclusión

El eje de simetría es un concepto fundamental en las matemáticas y la geometría, dividiendo las figuras y ecuaciones en mitades perfectamente reflejadas. Su ecuación, ya sea derivada mediante \(x = - \frac{b}{2a}\) para formas cuadráticas estándar o directamente desde el vértice, es una herramienta poderosa para analizar formas, resolver problemas y visualizar patrones.

Más allá de las matemáticas, el eje de simetría tiene aplicaciones prácticas en campos como la física, la arquitectura y la ingeniería, sustentando diseños que son no solo funcionales sino también visualmente armoniosos. Al dominar este concepto, obtienes una comprensión de la elegancia de la simetría y su impacto tanto en la teoría como en las aplicaciones del mundo real, cerrando la brecha entre el cálculo y la creatividad.

Referencia:

https://insights.jonite.com/the-art-of-symmetry-in-architecture

https://mfaizan.github.io/2022/10/02/symmetry.html

https://shs.hal.science/halshs-03048686v1/file/20030.pdf