What Is Fibonacci Sequence?

Have you been mesmerised by the elegant architecture of Greece's Parthenon? This iconic masterpiece is widely believed to reflect its golden ratio—an intriguing mathematical concept linked with the Fibonacci Sequence—as evidenced in its golden ratio structure.

Starting from zero and one, the Fibonacci Sequence grows as each number adds the sum of two previous ones--an astonishingly simple yet remarkable process. Not surprisingly, its relationship to natural and artistic masterpieces such as sunflower seed arrangements, spiraled seashells, or elegant proportions of architecture is deep. This article will examine its rich history, captivating patterns, mathematical essence and numerous applications throughout various fields.

The History and Impact of Fibonacci Sequence

The Sequence's Origins and Spread

The Fibonacci Sequence can be traced to ancient India, around 200 BCE, in the mathematical text Ganitasarasangraha. At first, it was used to analyze poetic meters and syllable patterns - providing an innovative fusion between mathematics and language analysis. Later, it came to be known as "Matrameru" in Sanskrit for exploring rhythmic combinations.

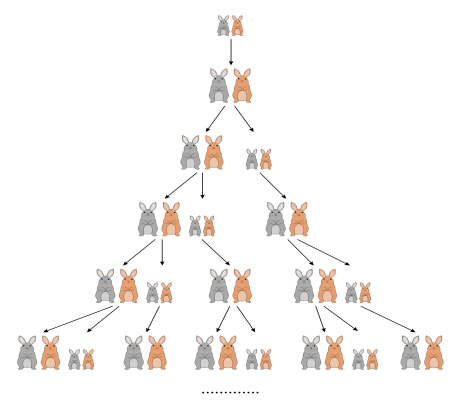
However, in 1202 CE it was first officially introduced to Western culture by Italian mathematician Leonardo Fibonacci's book Liber Abaci (The Book of Calculation). His illustration for it used a common problem regarding rabbit reproduction as a metaphor: how many pairs will emerge if each reproduced every month beginning at their second month? His solution produced the sequence: 0, 1, 1, 2, 3, 5, 8,...

Fibonacci used this practical yet profound problem to demonstrate the versatility of his sequence while also introducing Europe to advanced mathematical techniques developed in India and Arabia, providing a foundation for the further growth of number theory and series theory.

Fibonacci's Contributions and Legacy

Leonardo Fibonacci made significant contributions beyond introducing the sequence. His support of the Hindu-Arabic numeral system - with its revolutionary use of "0," for instance - helped Europe move away from Roman numeral calculations and to greater efficiency when performing trade, banking and scientific calculations, marking the dawn of modern mathematics era.

The Fibonacci Sequence bridged the gap between natural elements and human creativity, inspiring innovations both scientific and artistic alike. Fibonacci Sequence revealed intricate natural patterns such as spirals in shells or leaf arrangements in plants; its connection to the Golden Ratio led to advances in art and architecture as it combined mathematical harmony with aesthetic beauty in designs that balanced mathematical harmony with aesthetic beauty. Fibonacci was also known for bridging nature with human creativity to inspire advances, both scientific and artistic, in every form.

Cultural and Natural Phenomena

Fibonacci Sequence in Literature and Art

The Fibonacci Sequence is more than an academic concept; it serves as both artistic and literary themes, most famously in Dan Brown's best-selling novel The Da Vinci Code where it becomes one of several clues for solving mysteries. By weaving mathematics into fiction, this novel publicized its application and significance - sparking interest about their practical applications and significance among readers everywhere.

Artists frequently associate the Fibonacci Sequence with its mathematical offshoot, the Golden Ratio. This proportion, approximately 1.618, has long been employed in paintings, sculptures and architecture composition. Renaissance artists such as Leonardo da Vinci are believed to have utilized mathematical principles like this for works such as The Last Supper and Vitruvian Man - adding depth and balance while increasing visual appeal of these masterpieces.

Modern artists and designers continue to find great motivation from the Fibonacci Sequence and Golden Ratio, using it for everything from painting canvasses, photographing sets or designing user interfaces for digital platforms - its combination of mathematical precision with artistic creativity demonstrates its relevance across disciplines.

The Fibonacci Sequence in Nature

The Fibonacci Sequence can be seen throughout nature, revealing its mathematical roots in organic forms such as sunflower seeds. Sunflower seeds grow in spirals reminiscent of its mathematical basis - often matching up with successive Fibonacci numbers (34 or 55 for instance), providing efficient packing and optimal use of space.

Pinecones feature Fibonacci spirals in their scales to maximize seed protection and distribution, while spiral shells like those belonging to the Nautilus grow using an expansion pattern called the Golden Spiral, which derives from Fibonacci Sequence geometry. This growth pattern allows an organism to expand proportionally while maintaining structural integrity.

Nature is abundant with patterns related to Fibonacci numbers that don't just reflect coincidence; rather they point out how living systems use energy and space efficiently. This natural efficiency has inspired biomimicry in various fields where researchers and designers borrow principles from nature in order to solve engineering or environmental challenges.

Fibonacci Sequence Overview

Definition and Rules

What Is the Fibonacci Sequence?

The Fibonacci Sequence is an endless series of numbers starting at zero and one, in which each successive number represents the sum of its two predecessors. Mathematically speaking, its definition can be stated as follows:

\(F_n = F_{n-1} + F_{n-2}, \quad n \geq 2\)

With seed values:  

\(F_0 = 0, \quad F_1 = 1\)

This recursive sequence produces an infinite set of numbers:  

\(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \dots\)  

Though its foundation lies in simple addition, this sequence displays complex relationships with nature, mathematics and design principles - particularly its golden ratio linkage. This sequence has become well known due to its prevalence across numerous fields as well as for being linked with it.

Basic Rules and the First 10 Terms  

The Fibonacci Sequence's formation follows simple rules. Below are its initial 10 terms generated using its recursive formula:

\(\begin{aligned} &F_0 = 0, \\ &F_1 = 1, \\ &F_2 = F_1 + F_0 = 1, \\ &F_3 = F_2 + F_1 = 2, \\ &F_4 = F_3 + F_2 = 3, \\ &F_5 = F_4 + F_3 = 5, \\ &F_6 = F_5 + F_4 = 8, \\ &F_7 = F_6 + F_5 = 13, \\ &F_8 = F_7 + F_6 = 21, \\ &F_9 = F_8 + F_7 = 34. \end{aligned}\)

As the numbers increase, their mathematical properties begin to emerge: such as their relation to the Golden Ratio or even being present in real-life phenomena.

Features of the Sequence

The Fibonacci Sequence displays remarkable patterns that have proven essential in mathematics, science, and art. Some notable characteristics are:

1. Divisibility Properties: Every third Fibonacci number is divisible by 2 and every fourth by three; as well as this property, all of the subsequent Fibonacci numbers have this property as well.

2. Ratios Approaching the Golden Ratio: Beginning with the third term, the ratio of consecutive Fibonacci numbers (e.g., \(\frac{F_8}{F_7} = \frac{21}{13} \approx 1.615\)) gradually converges to the Golden Ratio (\(\phi \approx 1.618\)).  

3. Unique Growth Properties: The sequence develops exponentially, its rate being intrinsically tied to the Golden Ratio.

These properties of Fibonacci ratios have led to its wide application in nature and human-made designs alike, from nature to architecture, from optimization processes and aesthetic arrangements to recursive programming patterns - showing its elegance of mathematics in their use. Fibonacci stands as an embodiment of simplicity and brilliance at once!

Fibonacci in Mathematical Principles  

Recursive Formula

Seed Values and Recursive Formula

The Fibonacci Sequence can be generated using an easy recursive formula:

\(F_n = F_{n-1} + F_{n-2}, \quad n \geq 2\)  

Where the seed values are defined as:  

\(F_0 = 0, \quad F_1 = 1\)  

This formula shows how each term in the sequence represents the sum of two preceding terms, such as in this instance:

\(F_2 = F_1 + F_0 = 1, \quad F_3 = F_2 + F_1 = 2, \quad F_4 = F_3 + F_2 = 3, \quad F_5 = F_4 + F_3 = 5\)  

This recursive structure displays the beauty of mathematical growth and serves as an indispensable concept in understanding recursive algorithms.

Challenges in Recursive Computation

While using recursive formulae may seem simple and intuitive, inefficient use of them when computing large Fibonacci numbers becomes apparent. Each term relies on all previous terms being calculated before it, leading to exponential time complexity\(O(2^n)\). Calculating \(F_{50}\) would require millions of repeated calculations of intermediate terms like \(F_{48}\) and \(F_{49}\). in order to reach its completion.

Dynamic programming offers an efficient alternative by memoizing previously computed terms (memoization), decreasing time complexity to linear \(O(n)\). Another effective approach is iterative calculations, which avoid recursion altogether and allow faster calculation of higher terms. Both techniques have applications beyond computer science.

Golden Ratio Calculations

Relationship Between Fibonacci and the Golden Ratio

The Fibonacci Sequence exhibits an extraordinary relationship to the Golden Ratio, known as \(\phi\) (approximately 1.618). Mathematically speaking, this ratio can be expressed as:

\(\phi = \frac{1 + \sqrt{5}}{2}\)  

As the Fibonacci Sequence progresses, the ratio of consecutive terms (\(\frac{F_{n}}{F_{n-1}}\)) approaches \(\phi\). For instance:  

\(\frac{F_8}{F_7} = \frac{21}{13} \approx 1.615, \quad \frac{F_9}{F_8} = \frac{34}{21} \approx 1.619\)  

This convergence demonstrates how a sequence reflects the harmony found throughout nature and design. This phenomenon has led to widespread usage of the Golden Ratio as an aesthetic approach in disciplines like architecture and art due to its pleasing properties.

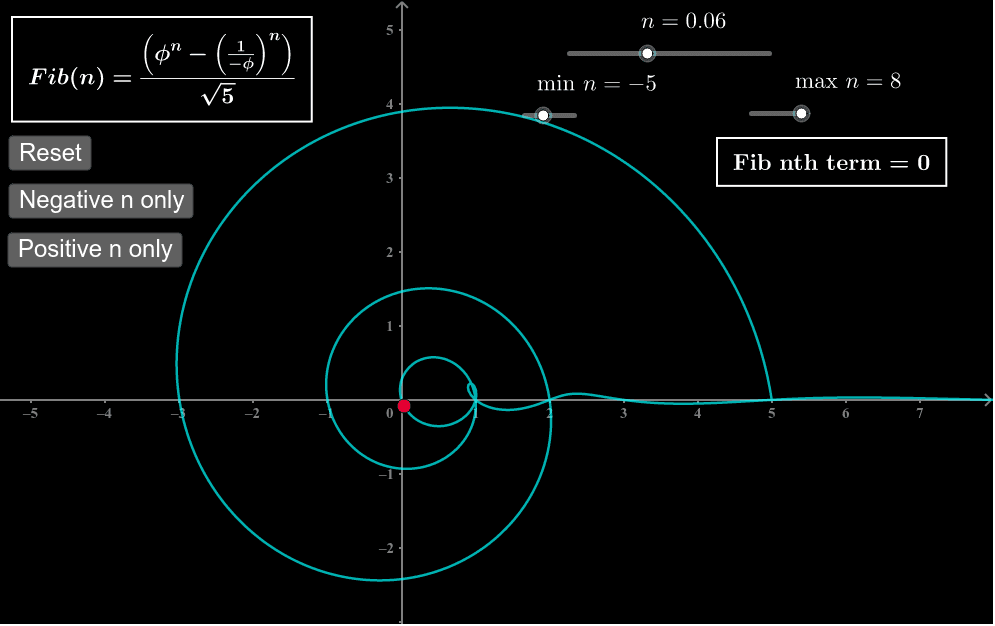
Binet's Formula for Fast Calculation

Binet's Formula provides an elegant closed-form expression for directly calculating any Fibonacci number without recourse to recursive algorithms:

\(F_n = \frac{\phi^n - (1-\phi)^n}{\sqrt{5}}\)  

Here:  

- \(\phi\) is the Golden Ratio (\(\phi \approx 1.618\))  

- \(1-\phi \approx -0.618\)  

At large \(n\) values, the term \((1-\phi)^n\) approaches zero quickly allowing a simplified approximate calculation:

\(F_n \approx \frac{\phi^n}{\sqrt{5}}\)  

For example, using Binet’s formula to calculate \(F_{10}\):  

\(F_{10} = \frac{\phi^{10} - (1-\phi)^{10}}{\sqrt{5}} \approx 55\)  

This formula is especially effective at quickly and accurately calculating large Fibonacci numbers without iterative or recursive steps.

Derivation and Approximation of the Formula

Binet's formula can be obtained by solving and substituting into linear recurrence relations the characteristic equation for recursive definition\(x^2 - x - 1 = 0\), with roots of \(\phi\) and \(1-\phi\). When solved and substituted into the general solution for linear recurrence relations, Binet's formula emerges; for practical applications, its approximation for large numbers such as "n" also offers quick estimates of Fibonacci numbers.

If you have any more sequence-related questions, you can ask them in our app or question bank.

Fibonacci in Art and Design

Golden Ratio in Design

Architecture and Visual Harmony

The Fibonacci Sequence and Golden Ratio have profoundly shaped architectural design, providing a mathematical basis for symmetry and proportion in architecture. One such structure that exhibits this relationship is The Parthenon in Greece; its height-to-width ratio approaches that of the Golden Ratio; this subtle relationship creates an inviting visual experience while heightening the aesthetic value of this building.

Modern architects frequently employ Fibonacci numbers when crafting spaces that feel balanced and harmonious, using dimensions such as 8 meters by 13 meters or 13 meters by 21 meters that harmonize with these sequences.

Natural Spirals in Design

The Golden Spiral, inspired by Fibonacci numbers, serves as an essential visual design element. Constructed from plotting quarter circles through squares with side lengths matching those found in Fibonacci numbers, this spiral appears both naturally (e.g. nautilus shells) and in graphic design and photography where it helps arrange elements dynamically.

Artists and designers employ the Golden Spiral in their compositions to help guide the viewer's attention naturally, creating balance and flow. From paintings, logos, to website layouts - Fibonacci spirals add an organic elegance that only nature could provide.

Fibonacci in Modern Applications

Finance and Modeling

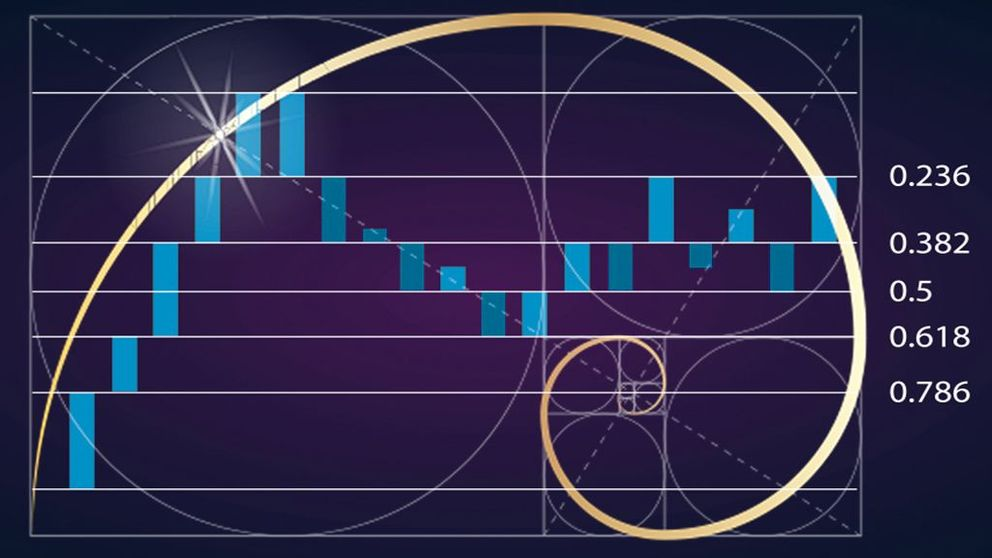
Fibonacci Retracement in Technical Analysis

Fibonacci Retracement is an invaluable financial market tool that identifies potential levels of support and resistance during price trends. By employing Fibonacci ratios such as 23.6%, 38.2%, 50% and 61.8% to determine how likely a price reverse will occur within a trend--these levels correspond with ratios derived from sequence.

Fibonacci levels combine mathematical precision with market dynamics to increase predictive accuracy in trading strategies and enhance predictive accuracy in trading strategies. Traders might expect that, should a stock quickly increase from 100 to 200, it might retrace and stabilize near 161.8 or142.2 as it nears $200 again using Fibonacci levels for greater predictive accuracy and market dynamics. This method provides predictive accuracy through mathematical precision combined with market dynamics.

Extensions in Forecasting and Patterns

Fibonacci extensions provide useful price targets beyond retracement levels in strong trends, for instance, extending up to 161.8% of an initial move using Fibonacci ratios. Elliott Wave Theory relies heavily on Fibonacci numbers to aid in forecasting market cycles - often rising and corrective waves have durations defined by Fibonacci numbers such as 3, 5, or 8 cycles.

Applications in Computer Science

Using Fibonacci for Optimizing Cache and Storage

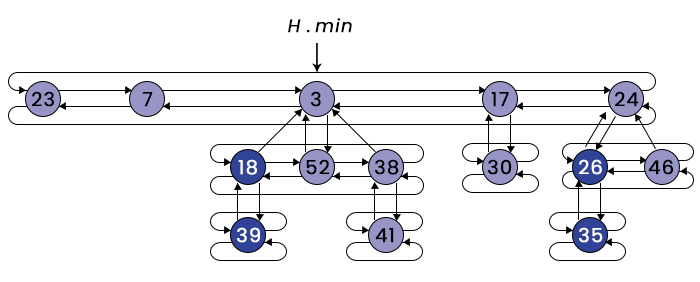
Fibonacci principles can be seen throughout computer science in both algorithms and data structure design, with priority queue structures such as "Fibonacci Heap" using them as priority queue structures that optimize operations like insertion and merging; its time complexity being \(O(\log n)\)allowing this structure to improve efficiency for algorithms like Dijkstra's Shortest Path or Prim's Minimum Spanning Tree algorithms.

Fibonacci numbers can also help solve memory allocation problems by breaking memory into block sizes that follow fibonacci numbers, helping systems reduce fragmentation and allocate resources more effectively. Furthermore, Fibonacci Search enhances binary search algorithms by segmenting arrays into fibonacci-sized segments in order to minimize comparisons while simultaneously improving performance.

If necessary, you can look at other sequence to enrich your knowledge, such as the detailed concepts and applications of arithmetic sequence and geometric sequence.

Fibonacci's Sequence can be found everywhere from Parthenon architecture to sunflower seeds; from art galleries to financial market predictions. Starting from zero and one, this mathematical pattern illuminates nature and human creation alike with its extraordinary beauty. From history, art, biology and design projects alike; his legacy stands as a link between creativity and logic that reminds us mathematics is not simply numbers but part of nature itself; shaping it in astonishing ways that touch all aspects of our world in fascinating ways.

reference：

https://en.wikipedia.org/wiki/Fibonacci_sequence

https://en.wikipedia.org/wiki/Golden_ratio

https://en.wikipedia.org/wiki/Fibonacci_retracement