¿Qué es la secuencia de Fibonacci?

¿Te has sentido fascinado por la elegante arquitectura del Partenón de Grecia? Se cree ampliamente que esta obra maestra icónica refleja su proporción áurea, un intrigante concepto matemático relacionado con la Secuencia de Fibonacci, como lo evidencia su estructura de proporción áurea.

Comenzando desde cero y uno, la Secuencia de Fibonacci crece a medida que cada número suma el total de los dos anteriores, un proceso asombrosamente simple pero notable. No es sorprendente que su relación con obras maestras naturales y artísticas como los arreglos de semillas de girasol, los caracoles en espiral o las elegantes proporciones de la arquitectura sea profunda. Este artículo examinará su rica historia, sus patrones cautivadores, su esencia matemática y sus numerosas aplicaciones en varios campos.

La Historia e Impacto de la Secuencia de Fibonacci

Los Orígenes y la Difusión de la Secuencia

La Secuencia de Fibonacci se remonta a la antigua India, alrededor del año 200 a.C., en el texto matemático Ganitasarasangraha. Al principio, se utilizó para analizar los metros poéticos y los patrones silábicos, proporcionando una fusión innovadora entre matemáticas y análisis del lenguaje. Más tarde, se conoció como "Matrameru" en sánscrito para explorar combinaciones rítmicas.

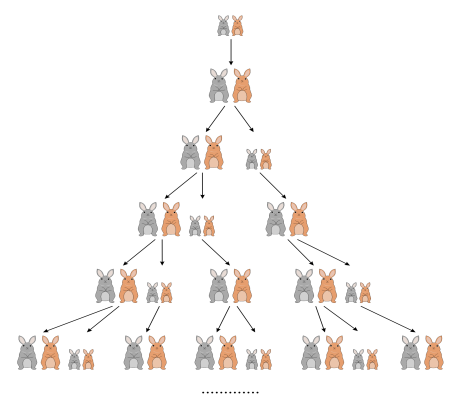
Sin embargo, en el año 1202 d.C., fue introducida oficialmente a la cultura occidental por el matemático italiano Leonardo Fibonacci en su libro Liber Abaci (El Libro del Cálculo). Su ilustración usó un problema común sobre la reproducción de conejos como metáfora: ¿cuántas parejas surgirán si cada una se reproduce cada mes comenzando en su segundo mes? Su solución produjo la secuencia: 0, 1, 1, 2, 3, 5, 8,...

Fibonacci utilizó este problema práctico pero profundo para demostrar la versatilidad de su secuencia, al mismo tiempo que introdujo a Europa técnicas matemáticas avanzadas desarrolladas en India y Arabia, proporcionando una base para el crecimiento adicional de la teoría de números y la teoría de series.

Contribuciones y Legado de Fibonacci

Leonardo Fibonacci hizo contribuciones significativas más allá de introducir la secuencia. Su apoyo al sistema de numeración hindú-arábigo -con su uso revolucionario del "0", por ejemplo- ayudó a Europa a alejarse de los cálculos con números romanos y a una mayor eficiencia al realizar cálculos de comercio, banca y científicos, marcando el comienzo de la era de las matemáticas modernas.

La Secuencia de Fibonacci unió los elementos naturales y la creatividad humana, inspirando innovaciones tanto científicas como artísticas por igual. La Secuencia de Fibonacci reveló intrincados patrones naturales como las espirales en las conchas o la disposición de las hojas en las plantas; su conexión con la Proporción Áurea llevó a avances en el arte y la arquitectura, ya que combinaba armonía matemática con belleza estética en diseños que equilibraban la armonía matemática con la belleza estética. Fibonacci también fue conocido por unir la naturaleza con la creatividad humana para inspirar avances, tanto científicos como artísticos, en cada forma.

Fenómenos Culturales y Naturales

Secuencia de Fibonacci en Literatura y Arte

La Secuencia de Fibonacci es más que un concepto académico; sirve como tema tanto artístico como literario, más famoso en la exitosa novela de Dan Brown El Código Da Vinci, donde se convierte en una de varias pistas para resolver misterios. Al entrelazar las matemáticas con la ficción, esta novela difundió su aplicación y significado, despertando el interés sobre sus aplicaciones prácticas y su importancia entre los lectores de todo el mundo.

Los artistas frecuentemente asocian la Secuencia de Fibonacci con su derivado matemático, la Proporción Áurea. Esta proporción, aproximadamente 1.618, ha sido empleada durante mucho tiempo en pinturas, esculturas y composición arquitectónica. Se cree que artistas del Renacimiento como Leonardo da Vinci utilizaron principios matemáticos como este para obras como La Última Cena y El Hombre de Vitruvio, añadiendo profundidad y equilibrio mientras incrementaban el atractivo visual de estas obras maestras.

Artistas y diseñadores modernos continúan encontrando gran motivación en la Secuencia de Fibonacci y la Proporción Áurea, usándola para todo, desde pintar lienzos, fotografiar sets o diseñar interfaces de usuario para plataformas digitales; su combinación de precisión matemática con creatividad artística demuestra su relevancia en diversas disciplinas.

La Secuencia de Fibonacci en la Naturaleza

La Secuencia de Fibonacci se puede ver a lo largo de la naturaleza, revelando sus raíces matemáticas en formas orgánicas como las semillas de girasol. Las semillas de girasol crecen en espirales que recuerdan su base matemática, a menudo coincidiendo con números sucesivos de Fibonacci (34 o 55, por ejemplo), proporcionando un empaquetado eficiente y un uso óptimo del espacio.

Las piñas presentan espirales de Fibonacci en sus escamas para maximizar la protección y distribución de las semillas, mientras que las conchas en espiral, como las del Nautilus, crecen utilizando un patrón de expansión llamado la Espiral Dorada, que se deriva de la geometría de la Secuencia de Fibonacci. Este patrón de crecimiento permite a un organismo expandirse proporcionalmente manteniendo su integridad estructural.

La naturaleza abunda en patrones relacionados con los números de Fibonacci que no solo reflejan coincidencia; más bien, señalan cómo los sistemas vivos usan la energía y el espacio de manera eficiente. Esta eficiencia natural ha inspirado la biomimética en varios campos donde investigadores y diseñadores toman principios de la naturaleza para resolver desafíos de ingeniería o ambientales.

Visión General de la Secuencia de Fibonacci

Definición y Reglas

¿Qué es la Secuencia de Fibonacci?

La Secuencia de Fibonacci es una serie infinita de números que comienza en cero y uno, en la cual cada número sucesivo representa la suma de sus dos predecesores. Matemáticamente hablando, su definición se puede expresar de la siguiente manera:

\(F_n = F_{n-1} + F_{n-2}, \quad n \geq 2\)

Con valores iniciales:  

\(F_0 = 0, \quad F_1 = 1\)

Esta secuencia recursiva produce un conjunto infinito de números:  

\(0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, \dots\)  

Aunque su fundamento radica en la simple adición, esta secuencia muestra complejas relaciones con la naturaleza, las matemáticas y principios de diseño - particularmente por su vinculación con la proporción áurea. Esta secuencia se ha hecho muy conocida debido a su prevalencia en numerosos campos, así como por estar vinculada a ella.

Reglas Básicas y los Primeros 10 Términos  

La formación de la Secuencia de Fibonacci sigue reglas simples. A continuación se presentan sus 10 términos iniciales generados usando su fórmula recursiva:

\(\begin{aligned} &F_0 = 0, \\ &F_1 = 1, \\ &F_2 = F_1 + F_0 = 1, \\ &F_3 = F_2 + F_1 = 2, \\ &F_4 = F_3 + F_2 = 3, \\ &F_5 = F_4 + F_3 = 5, \\ &F_6 = F_5 + F_4 = 8, \\ &F_7 = F_6 + F_5 = 13, \\ &F_8 = F_7 + F_6 = 21, \\ &F_9 = F_8 + F_7 = 34. \end{aligned}\)

A medida que los números aumentan, comienzan a emerger sus propiedades matemáticas: como su relación con la Proporción Áurea o incluso su presencia en fenómenos de la vida real.

Características de la Secuencia

La Secuencia de Fibonacci muestra patrones notables que han demostrado ser esenciales en matemáticas, ciencia y arte. Algunas características destacadas son:

1. Propiedades de Divisibilidad: Cada tercer número de Fibonacci es divisible por 2 y cada cuarto por tres; además, todas las subsecuentes números de Fibonacci tienen esta propiedad también.

2. Relaciones que Se Acercan a la Proporción Áurea: Comenzando con el tercer término, la razón de números consecutivos de Fibonacci (por ejemplo, \(\frac{F_8}{F_7} = \frac{21}{13} \approx 1.615\)) converge gradualmente hacia la Proporción Áurea (\(\phi \approx 1.618\)).  

3. Propiedades de Crecimiento Únicas: La secuencia se desarrolla exponencialmente, su tasa está intrínsecamente ligada a la Proporción Áurea.

Estas propiedades de las razones de Fibonacci han llevado a su amplia aplicación tanto en la naturaleza como en diseños hechos por el hombre, desde la naturaleza hasta la arquitectura, desde procesos de optimización y arreglos estéticos hasta patrones de programación recursiva - mostrando su elegancia matemática en su uso. ¡Fibonacci se erige como un emblema de simplicidad y brillantez a la vez!

Fibonacci en Principios Matemáticos  

Fórmula Recursiva

Valores Iniciales y Fórmula Recursiva

La Secuencia de Fibonacci puede generarse usando una sencilla fórmula recursiva:

\(F_n = F_{n-1} + F_{n-2}, \quad n \geq 2\)  

Donde los valores iniciales se definen como:  

\(F_0 = 0, \quad F_1 = 1\)  

Esta fórmula muestra cómo cada término de la secuencia representa la suma de los dos términos anteriores, como en este caso:

\(F_2 = F_1 + F_0 = 1, \quad F_3 = F_2 + F_1 = 2, \quad F_4 = F_3 + F_2 = 3, \quad F_5 = F_4 + F_3 = 5\)  

Esta estructura recursiva muestra la belleza del crecimiento matemático y sirve como un concepto indispensable para entender algoritmos recursivos.

Desafíos en el Cálculo Recursivo

Aunque usar fórmulas recursivas puede parecer simple e intuitivo, se hace evidente su uso ineficiente cuando se calculan números de Fibonacci grandes. Cada término depende de que todos los términos anteriores hayan sido calculados antes, lo que lleva a una complejidad de tiempo exponencial\(O(2^n)\). Calcular \(F_{50}\) requeriría millones de cálculos repetidos de términos intermedios como \(F_{48}\) y \(F_{49}\). para llegar a su finalización.

La programación dinámica ofrece una alternativa eficiente mediante la memorización de términos previamente calculados (memoización), disminuyendo la complejidad del tiempo a lineal \(O(n)\). Otro enfoque efectivo es el cálculo iterativo, que evita la recursión por completo y permite un cálculo más rápido de términos más altos. Ambas técnicas tienen aplicaciones más allá de la informática.

Cálculos de la Razón Áurea

Relación entre Fibonacci y la Razón Áurea

La Secuencia de Fibonacci exhibe una relación extraordinaria con la Razón Áurea, conocida como \(\phi\) (aproximadamente 1.618). Matemáticamente, esta razón puede expresarse como:

\(\phi = \frac{1 + \sqrt{5}}{2}\)  

A medida que la Secuencia de Fibonacci progresa, la razón de términos consecutivos (\(\frac{F_{n}}{F_{n-1}}\)) se aproxima a \(\phi\). Por ejemplo:  

\(\frac{F_8}{F_7} = \frac{21}{13} \approx 1.615, \quad \frac{F_9}{F_8} = \frac{34}{21} \approx 1.619\)  

Esta convergencia demuestra cómo una secuencia refleja la armonía encontrada en toda la naturaleza y el diseño. Este fenómeno ha llevado al uso extendido de la Razón Áurea como un enfoque estético en disciplinas como la arquitectura y el arte debido a sus propiedades agradables.

Fórmula de Binet para Cálculo Rápido

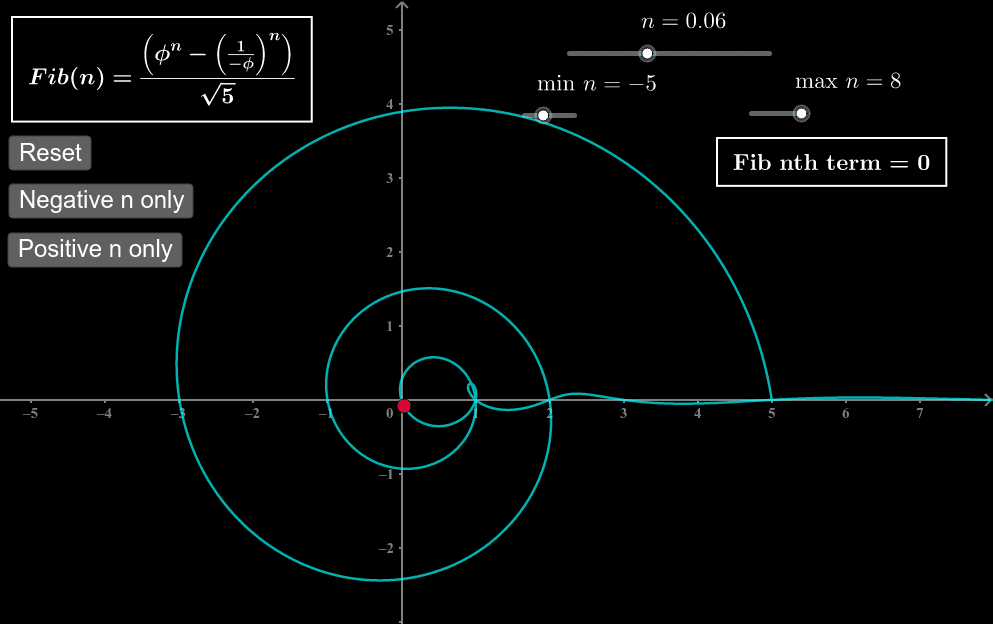
La Fórmula de Binet proporciona una expresión elegante de forma cerrada para calcular directamente cualquier número de Fibonacci sin necesidad de algoritmos recursivos:

\(F_n = \frac{\phi^n - (1-\phi)^n}{\sqrt{5}}\)  

Aquí:  

- \(\phi\) es la Razón Áurea (\(\phi \approx 1.618\))  

- \(1-\phi \approx -0.618\)  

Para valores grandes de \(n\), el término \((1-\phi)^n\) se aproxima rápidamente a cero permitiendo un cálculo aproximado simplificado:

\(F_n \approx \frac{\phi^n}{\sqrt{5}}\)  

Por ejemplo, utilizando la fórmula de Binet para calcular \(F_{10}\):  

\(F_{10} = \frac{\phi^{10} - (1-\phi)^{10}}{\sqrt{5}} \approx 55\)  

Esta fórmula es especialmente efectiva para calcular de forma rápida y precisa grandes números de Fibonacci sin pasos iterativos o recursivos.

Derivación y Aproximación de la Fórmula

La fórmula de Binet se puede obtener resolviendo y sustituyendo en relaciones de recurrencia lineal la ecuación característica para la definición recursiva\(x^2 - x - 1 = 0\), con raíces de \(\phi\) y \(1-\phi\). Al resolver y sustituir en la solución general para relaciones de recurrencia lineal, surge la fórmula de Binet; para aplicaciones prácticas, su aproximación para grandes números como "n" también ofrece estimaciones rápidas de números de Fibonacci.

Si tienes más preguntas relacionadas con secuencias, puedes hacerlas en nuestra aplicación o banco de preguntas.

Fibonacci en el Arte y el Diseño

Proporción Áurea en el Diseño

Arquitectura y Armonía Visual

La Secuencia de Fibonacci y la Proporción Áurea han influido profundamente en el diseño arquitectónico, proporcionando una base matemática para la simetría y la proporción en la arquitectura. Una de las estructuras que exhibe esta relación es el Partenón en Grecia; su relación altura-ancho se aproxima a la Proporción Áurea; esta relación sutil crea una experiencia visual atractiva al tiempo que aumenta el valor estético de este edificio.

Los arquitectos modernos utilizan frecuentemente los números de Fibonacci al diseñar espacios que se sienten equilibrados y armoniosos, utilizando dimensiones como 8 metros por 13 metros o 13 metros por 21 metros que armonizan con estas secuencias.

Espirales Naturales en el Diseño

La Espiral Áurea, inspirada en los números de Fibonacci, sirve como un elemento esencial en el diseño visual. Construida al trazar círculos de cuarto a través de cuadrados con longitudes de lado que coinciden con los encontrados en los números de Fibonacci, esta espiral aparece tanto de forma natural (por ejemplo, en caparazones de nautilus) como en diseño gráfico y fotografía, donde ayuda a organizar los elementos de manera dinámica.

Los artistas y diseñadores emplean la Espiral Áurea en sus composiciones para guiar naturalmente la atención del espectador, creando equilibrio y fluidez. Desde pinturas, logotipos, hasta diseños de sitios web - las espirales de Fibonacci aportan una elegancia orgánica que solo la naturaleza podría proporcionar.

Fibonacci en Aplicaciones Modernas

Finanzas y Modelado

Retrocesos de Fibonacci en el Análisis Técnico

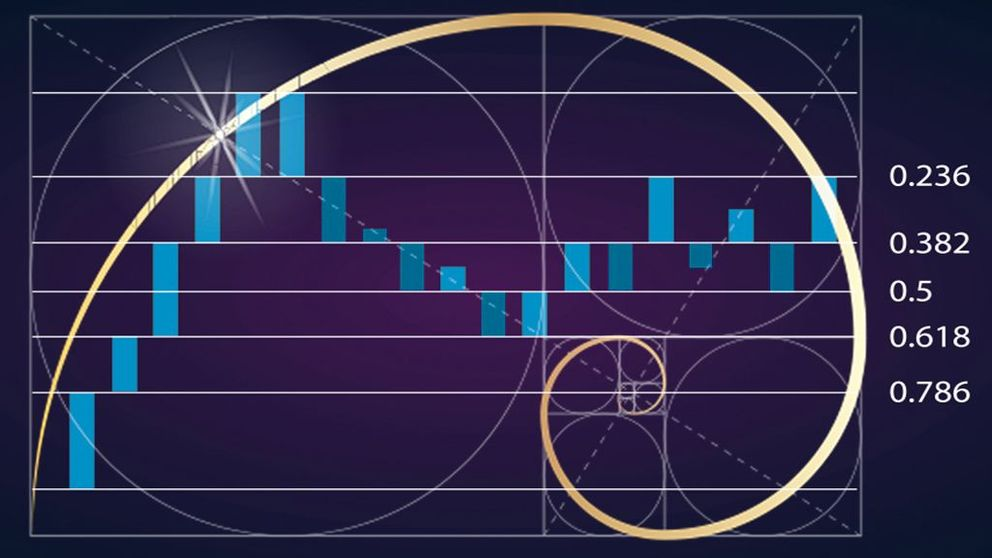
El Retroceso de Fibonacci es una herramienta invaluable del mercado financiero que identifica niveles potenciales de soporte y resistencia durante las tendencias de precios. Al emplear razones de Fibonacci como 23,6%, 38,2%, 50% y 61,8% para determinar qué tan probable es que ocurra un reverso de precios dentro de una tendencia, estos niveles corresponden con razones derivadas de la secuencia.

Los niveles de Fibonacci combinan precisión matemática con dinámicas de mercado para aumentar la exactitud predictiva en estrategias de trading y mejorar la exactitud predictiva en estrategias de trading. Los traders podrían esperar que, si una acción aumenta rápidamente de 100 a 200, podría retroceder y estabilizarse cerca de 161,8 o 142,2 mientras se acerca a $200 nuevamente usando niveles de Fibonacci para una mayor precisión predictiva y dinámicas de mercado. Este método proporciona exactitud predictiva a través de la precisión matemática combinada con dinámicas de mercado.

Extensiones en Pronósticos y Patrones

Las extensiones de Fibonacci proporcionan objetivos de precio útiles más allá de los niveles de retroceso en tendencias fuertes, por ejemplo, extendiéndose hasta el 161,8% de un movimiento inicial usando razones de Fibonacci. La Teoría de la Onda de Elliott se basa en gran medida en los números de Fibonacci para ayudar en el pronóstico de ciclos de mercado - a menudo las ondas ascendentes y correctivas tienen duraciones definidas por números de Fibonacci como 3, 5, o 8 ciclos.

Aplicaciones en Ciencias de la Computación

Usando Fibonacci para Optimización de Caché y Almacenamiento

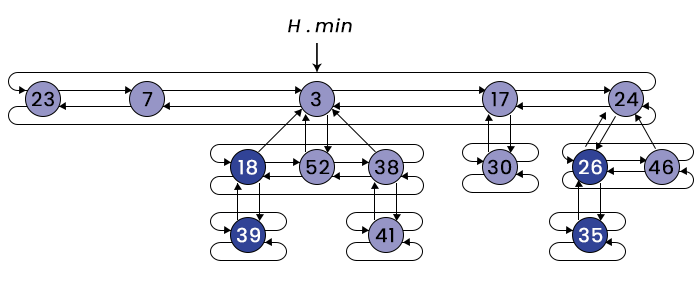
Los principios de Fibonacci se pueden ver a lo largo de la ciencia de la computación tanto en el diseño de algoritmos como de estructuras de datos, con estructuras de colas de prioridad tales como el "Fibonacci Heap" usándolas como estructuras de cola de prioridad que optimizan operaciones como inserción y fusión; su complejidad de tiempo es \(O(\log n)\)permitiendo que esta estructura mejore la eficiencia para algoritmos como los de Caminos Más Cortos de Dijkstra o Árbol de Cobertura Mínima de Prim.

Los números de Fibonacci también pueden ayudar a resolver problemas de asignación de memoria rompiendo la memoria en tamaños de bloques que siguen los números fibonacci, ayudando a los sistemas a reducir la fragmentación y asignar recursos de manera más efectiva. Además, la Búsqueda de Fibonacci mejora los algoritmos de búsqueda binaria al segmentar arrays en segmentos del tamaño de Fibonacci para minimizar comparaciones mientras mejora el rendimiento simultáneamente.

Si es necesario, puedes observar otras secuencias para enriquecer tu conocimiento, tales como los conceptos detallados y aplicaciones de la secuencia aritmética y la secuencia geométrica.

La Secuencia de Fibonacci se puede encontrar desde la arquitectura del Partenón hasta semillas de girasol; desde galerías de arte hasta predicciones de mercados financieros. Comenzando desde cero y uno, este patrón matemático ilumina tanto la naturaleza como la creación humana con su extraordinaria belleza. Desde la historia, arte, biología y proyectos de diseño por igual; su legado perdura como un enlace entre creatividad y lógica que nos recuerda que las matemáticas no son simplemente números, sino parte de la naturaleza misma; dándole forma de maneras asombrosas que tocan todos los aspectos de nuestro mundo de maneras fascinantes.

referencia：

https://en.wikipedia.org/wiki/Fibonacci_sequence

https://en.wikipedia.org/wiki/Golden_ratio

https://en.wikipedia.org/wiki/Fibonacci_retracement