How to Find the Area of a Circle?

Circles can be seen everywhere: clock faces, pizza edges, or the cross-section of Earth can all be considered circles from a mathematical viewpoint. Their areas provide us with key data about their size and scope. At times, it may be necessary to calculate the area of a circle to address real-life or engineering challenges, like designing the dimensions for a manhole cover or determining how much paint will cover an entire circular wall. Discovering this topic allows us not only to master mathematical concepts but also to appreciate their scientific and artistic worth. In the following article, we'll focus on exploring the area of a circle, including fundamental concepts, area formulae, derivation processes, and practical uses for circles.

The Basic Concepts of a Circle  

What Is a Circle  

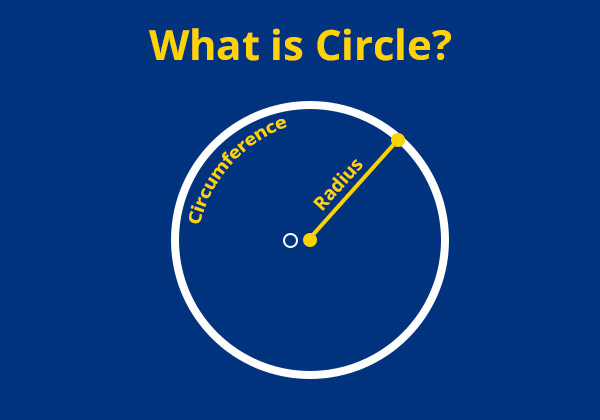
The circle is one of the simplest and classic figures in geometry. At its core, a circle is a plane figure in which all points are equally dispersed from an immoveable center point; these points constitute the "boundary" and this distance to its center point is known as its radius (r ). Circles can be found everywhere from daily contours to complex mathematical theories - making them essential tools in human understanding.

Though at first glance they appear simple, circles possess many properties. Their outside boundary is known as their "circumference"(C), while their full extension reveals another key parameter--its area (A ). Understanding these basic concepts will lead to further calculations and applications of circles.

Fun Mathematical Exploration of Circle Areas  

The History and Measurement Development of \(\pi\)  

\(\pi\)(pronounced “pi”) is an essential mathematical constant, denoting the ratio between circle circumference and diameter. It approximates 3.14159 but remains an irrational number with no definitive decimal expansion that repeats, giving \(\pi\) unique properties essential in formulae for the circumference/area of circles as well as in physical/engineering applications.

Discovering \(\pi\) has been an age-old pursuit; ancient Egyptians and Babylonians approximated its value around 2000 BCE through observation; Archimedes later used inscribed and circumscribed polygons to refine it further between 3.1408  and 3.1429 , with centuries later, Chinese mathematician Zu Chongzhi reaching unmatched precision over millennia when calculating it to seven decimal places achieving unrivalled precision over millennia!

Modern mathematicians such as Leibniz and Newton used infinite series to calculate\(\pi\), while advances in computing technology have extended its digits further still, supporting high-precision scientific research. \(\pi\) remains not only a mathematical icon but is a cornerstone of modern sciences and engineering research.

Circle Areas in Culture and Art  

Circles aren't simply mathematical concepts - they have deep cultural and aesthetic roots as well. Their form can be found everywhere, from planet shapes and their orbits around stars to ripples on water surfaces and sunbeam haloes, all of which contain circles! In art, circles symbolize harmony, completeness, and eternity, creating visual art with numbers as its base element.

Architecture often incorporates circular designs. Ancient Rome's Pantheon featured an eye-catching circular dome which highlighted both structural strength and geometric beauty, while Chinese culture emphasizes "round sky, square earth." Beijing Temple of Heaven's circular Hall of Prayer for Good Harvests symbolizes harmony and completeness as part of their mission statement.

Art is full of inspiration derived from circles. Leonardo da Vinci famously used circles during the Renaissance period in his Vittruvian Man_to demonstrate this relationship between circles, squares, and human proportions to emphasize geometry's role in art. While contemporary abstract artwork often uses circles as an artistic means to convey messages of peace and unity.

Symbolically, circles appear throughout Western philosophy and religion. Buddhist mandalas with intricate circular designs symbolically symbolize the center of our universe, while Western thought views circles as emblematic of perfection and infinity - reflecting a deep correlation between circular geometry and humanity's perceptions of reality.

The Formula for the Area of a Circle  

Definition of Area  

Geometry defines "area" as the area occupied by closed shapes on a plane; specifically, area measures how much of that plane region each point occupies within it. A circle covers an "area," representing its numerical value covering this particular plane region - this term not only forms the cornerstone of mathematics but is also central in practical and engineering applications.

Definition and calculation of area are instrumental to solving real-life issues related to circle areas. A gardener might need to estimate how much land area they require for planting in their circular flower bed; or designers can calculate table surface areas so as to design appropriate patterns on them. All these questions rely on accurate calculation of areas.

The area is usually measured in square units such as centimeters squared (\(\text{cm}^2\)) or square meters (\(\text{m}^2\)). Such measurements provide intuitive quantitative meaning that facilitates broader application; by studying area, we gain greater insight into spatial attributes and the mathematical essence of geometric forms, laying the groundwork for formulae derivation.

Formula for Calculating Area  

Formula Based on Radius  

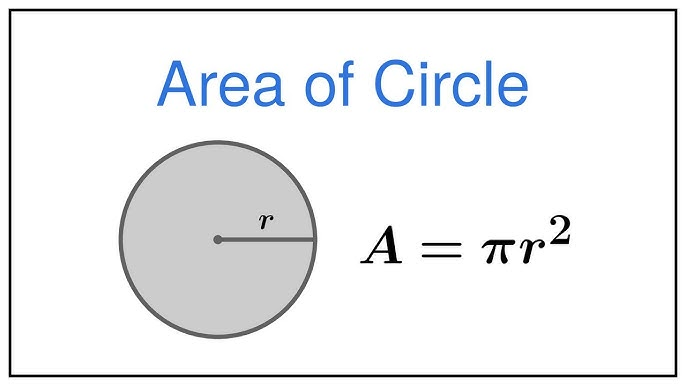
A classic formula to calculate the area of a circle can be expressed using its radius as follows:

\[A = πr^2\]  Where\(A\) denotes its area.

- \(π\) represents the mathematical constant pi (\(\approx 3.14159\)),  

- \(r\) is the radius of the circle.  

This formula indicates that the area of any circle is directly proportional to its square radius, making this foundational formula one of the easiest formulas to memorize and apply in everyday situations.

Formula Based on Diameter  

Since diameter (\(D\)) is twice that of radius (\(D = 2r\)), in the area formula, it can easily be substituted with the diameter and become:

\[A = \frac{πD^2}{4}\]

This equation can be especially useful for directly calculating an area when given its diameter, such as when estimating cross-sectional area in pipes based on inner diameter alone.

Formula Based on Circumference  

When one knows the circumference (\(C\)) of a circle, one can also calculate its area:

\[A = \frac{C^2}{4π}\]This formula can help solve issues involving circumference calculations, like determining how much land area a circular fence encloses after measuring its perimeter.

Overall, formulas provide flexible solutions for various scenarios and enable efficient applications depending on the data provided.

Relationships Between Different Formulas  

Formulas for the area of a circle may appear distinct; however, they are actually created through mathematical substitutions and transformations, adapting it to specific parameters. Starting from the formula based on radius \(A = πr^2\), we can derive other variants by substituting relationships among radius, diameter, and circumference parameters; substituting relationships such as double radius to make this adjustment yields:

\[A = \frac{πD^2}{4}\]This proves the consistency between formulae based on diameter and radius, using diameter-derived numbers or radius-derived numbers, respectively.

Similarly, using the circumference formula \(C = 2πr\), we can express the radius as \(r = \frac{C}{2π}\). Substituting into the area formula, we have:  

\[A = \frac{C^2}{4π}\]Derivations allow us to appreciate mathematics' abstract elegance while providing practical insight. When given information is not sufficient for an exact radius calculation, clever conversion may provide accurate solutions based on what information exists—all while adding beauty and functionality to mathematics!

The Derivation Process of the Area Formula  

Derivation Using the Area of a Rectangle  

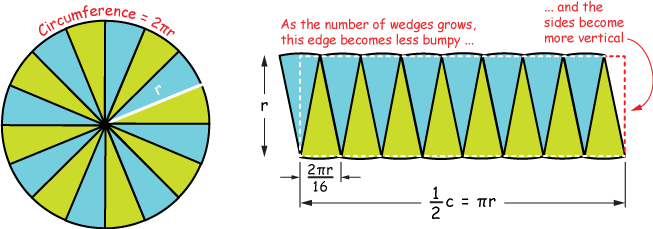
Formula for Area of Circle can be determined by transforming it into different geometric forms; one intuitive method being to use a rectangle as our starting point. We can do this by splitting up a circle into several equal parts and rearrange these parts until we achieve an effect which resembles that of a rectangle shape.

Assume a circle has an initial radius of ( r ), is divided into equal segments using wedge-cutters to cut it up evenly into divisions, then alternates from upright to inverted position (one upright, the next inverted)in an attempt to form something approximating a rectangle shape. As more divisions occur, it gets closer and closer.

The width of this rectangle equals the radius \(r\), and its length is approximately half the circumference of the circle, i.e., \(πr\). Hence, the area of the rectangle can be calculated as:  

\[\text{Area} = \text{width} × \text{length} = r × πr = πr^2\]With this reasoning in hand, we arrive at the formula \(A = πr^2\) for circle areas: their area equals the square of their radius multiplied by π. This method conforms with intuition while simultaneously emphasizing its geometric foundations.

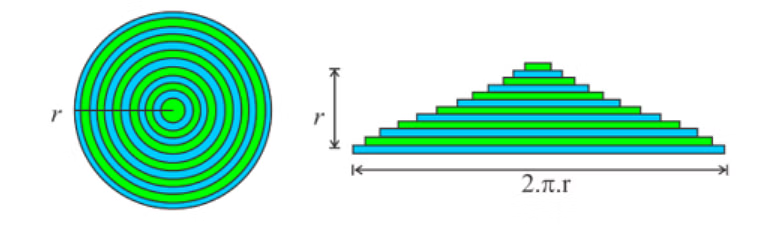
Derivation Using the Area of a Triangle  

One approach for deriving the formula involves the area of a triangle. Similar to rectangle derivation, this method also divides a circle into multiple wedges or sectors and rearranges them so as to approximate a triangle shape, thus turning your problem into the calculation of triangle's area.

Assume a circle with radius \(r\)and circumference \(C = 2πr\) has equal sectors \(n\) in which their height corresponds with \(r\), when these sectors are alternated arranged they approximate an isosceles triangle shape.

For this triangle, the height equals the circle’s radius \(r\), and the base is the circle’s circumference \(C\). Using the formula for the area of a triangle, we have:  

\[\text{Area} = \frac{\text{base} × \text{height}}{2} = \frac{C × r}{2} = \frac{2πr × r}{2} = πr^2\]This derivation subtly connects the area formula back to fundamental relationships among circle's geometric properties, reinforcing both accuracy and intuitiveness of formula\(A = πr^2\).

Comparison Between Circle Areas and Other Geometric Shapes  

Comparison Between Circle Areas and Square Areas  

Circles and squares are among the most familiar geometric forms we encounter daily, prompting many comparisons of their areas in daily life. For example, if a square with side length \(s\) has a diagonal equal to the diameter of a circle, the areas of the two shapes exhibit distinct differences.  

Assume the circle’s diameter is \(D\), and thus its area is:  

\[A = πr^2 = π(\frac{D}{2})^2 = \frac{πD^2}{4}\]The area of the square, meanwhile, is given by \(s^2\). Since the diagonal of the square is \(\sqrt{2}s\), and this equals the circle’s diameter \(D\), we have \(\sqrt{2}s = D\), or \(s = \frac{D}{\sqrt{2}}\). Thus, the area of the square becomes:  

\[\text{Area} = (\frac{D}{\sqrt{2}})^2 = \frac{D^2}{2}\]Comparing them side-by-side reveals that the circle's area is approximately 1.57 times that of its square counterpart - meaning, with equal diagonal length usage, circles more efficiently utilize space than squares do. This has practical applications in design and engineering applications such as using circular objects for materials conservation while simultaneously guaranteeing uniform stress distribution.

Relationship Between Circle Areas and Triangle Areas  

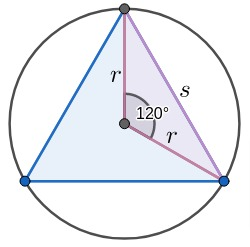
Compare circle areas and triangle areas using inscribed or circumscribed triangles. Consider an equilateral triangle inscribed into a circle with radius (r ). The side length of the triangle is \(a\), and its area can be calculated using the standard formula:  

\[\text{Area} = \frac{\sqrt{3}}{4}a^2\]

Since the side length \(a\) of the equilateral triangle satisfies \(a = \sqrt{3}r\), substituting this into the formula gives:  

\[\text{Area} = \frac{\sqrt{3}}{4} (\sqrt{3}r)^2 = \frac{3\sqrt{3}r^2}{4}\]By comparison, the area of a circle is approximately \(πr^2\); by taking into account dimensions \(π ≈ 3.14159\) and \(\sqrt{3} ≈ 1.732\)into consideration, an inscribed equilateral triangle's area is estimated at 0.83 times that of its circle-an indication that circular shapes provide superior coverage when it comes to geometric figures. Such comparisons provide further insights into their effectiveness as geometric forms.

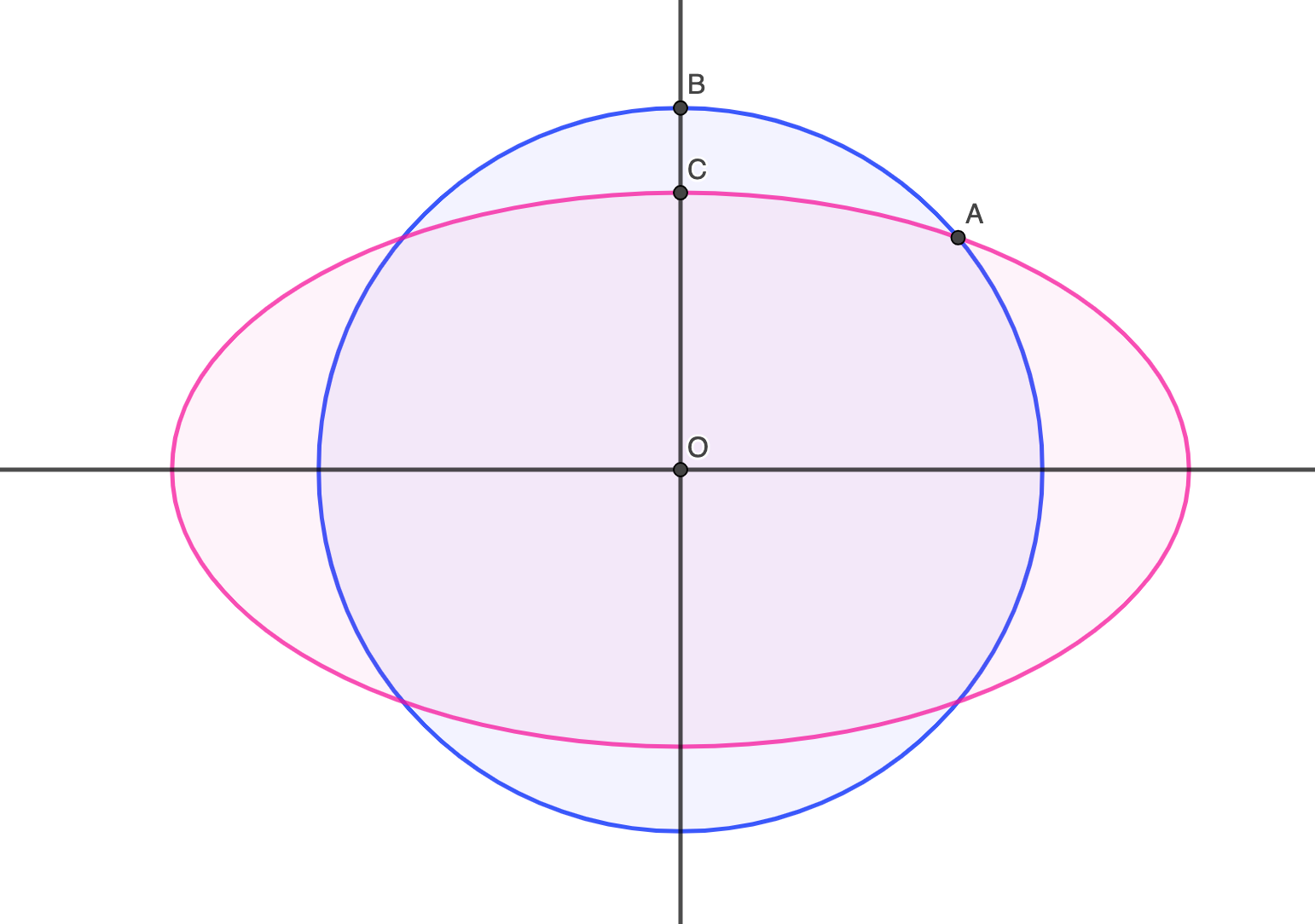
Comparison Between Circle Areas and Ellipse Areas  

An ellipse can be thought of as being a stretched-out version of a circle; its area formula reads as:

\[A = πab\]where \(a\) and \(b\) are the lengths of the ellipse’s semi-major and semi-minor axes, respectively. When these equal each other out \(a = b = r\), an ellipse becomes a circle, and its area formula becomes simplified as follows: \(A = πr^2\). Hence, a circle can be regarded as a special case of an ellipse.  

When the semi-major and semi-minor axes do not match up perfectly, ellipses display distinct differences from circular areas with similar radiuses in terms of area coverage; specific differences depend on values for \(a\) and \(b\). An ellipse's variation reflects these geometric transformations directly through its area variation.

Ellipses also play an essential part in practical applications. Planetary orbits tend to follow an elliptical shape, making the ellipse area formula an invaluable asset when solving astronomy issues. Comparing circles to ellipses highlights both geometric relationships as well as their importance within theoretical and applied sciences.

Common Questions and Solutions in Circle Area Calculations  

Balancing Precision and Approximation in Calculations  

Mathematically speaking, while we can express the area of a circle as\(A = πr^2\), in practical applications, this cannot always be accomplished with precision due to \(\pi\)'s infinite decimal places; therefore, we often need to use an approximate value instead. Two commonly used approximations for \(\pi\) are \(π \approx 3.14\) and the fractional value \(\frac{22}{7}\).  

As soon as calculating an area of a circular flower bed requires low accuracy requirements, an approximate value such as 3.14 may suffice in producing an approximation result. On the other hand, for high-precision engineering projects - like spacecraft orbit planning or instrument manufacturing - more decimal places of p or computational software may be needed to produce accurate results. Standard situations, like exams or instructional settings, typically specify approximations for \(\pi\) that calculations should follow accordingly.   

Precision and efficiency reflect each other in an inherent trade off: computational speed vs result accuracy. Simplifying p can speed manual calculations for basic problems while modern tools like programming or scientific calculators offer optimal accuracy without slowing efficiency. When dealing with approximations practices, understanding context and required precision is vital in finding an acceptable equilibrium point.

Division Methods for Complex Circular Structures  

Real-world applications frequently involve irregular or complex circular structures that cannot be solved with one formula alone, such as partial circular sectors, overlapped circles, or multiple combined circular shapes. Solving such situations often means breaking them up into more manageable sections to divide up into simpler circular regions or other shapes that make sense to solve.

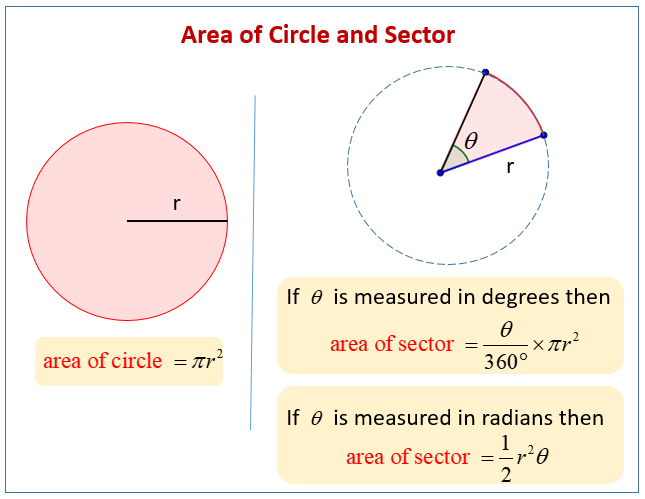
An effective approach for simplifying complex shapes is to divide them up into simple geometrical forms or sectors and calculate their areas before adding everything up. An example from our question bank, when breaking apart a circle into equal sectors or sections, calculate their areas using this formula:

\[A_{\text{sector}} = \frac{\theta}{360} × πr^2\]  where \(\theta\) represents the central angle of the sector.  

Complex situations, like calculating the intersection area between two overlapping circles, often necessitate more sophisticated methods involving geometry or integration—methods that demand higher mathematical knowledge levels from their users.

Dividing methods are widely employed for engineering solutions, including finding the area of a plate with holes by first calculating its total area and subtracting those for circular holes. Step-by-step division strategies simplify complex calculations while decreasing the chances of error and making calculations simpler overall.

Comparison Between Calculation Tools and Manual Calculation  

Circular area determination has become much easier in recent times thanks to various computational tools that make circle area calculations faster and more precise, including scientific calculators, mathematical software packages, and smartphone apps that conduct complex area calculations with high precision. Still, manual calculations still hold great value within educational learning or scenarios that call for theoretical validation.

Computational tools offer many distinct advantages. On one hand, they can significantly increase calculation efficiency—be it dealing with complex numbers or derivations of lengthy formulae—while simultaneously eliminating human errors from manual computation processes. Software such as MATLAB or Python provides multilayered formula solutions more quickly, making these devices essential in engineering fields.

However, complete reliance on tools also has drawbacks; without the necessary understanding, users might struggle to spot errors from incorrect input. Manual calculations offer users opportunities for deeper comprehension of mathematical principles, while step-by-step computation helps strengthen formula derivation, allowing flexible application across scenarios.

Computational tools and manual calculations work together to provide speed and precision when dealing with most real-world issues, while hand calculations remain essential in developing logic thinking and theoretical comprehension.

Studies of circle areas range from studying mathematical formulae to investigating their cultural, artistic, and practical uses - showing an intricate connection between theory and practice. By investigating foundational structures of circles as well as area formulae and various derivation methods we not only gain a firm grasp on geometric mathematical theory, but can observe its use across engineering design cultures such as design vs culture.

As an ideal geometric shape, circles not only offer visual beauty, but can also offer elegant solutions to numerous problems in everyday life. Learning the calculation of circle areas not only solves specific issues but also strengthens our logical thinking and abstraction skills - we hope that this article inspires readers to delve into more mathematical mysteries surrounding circles; let's embrace all their endless mathematical applications!

reference:

https://en.wikipedia.org/wiki/Circle

https://en.wikipedia.org/wiki/Area

https://en.wikipedia.org/wiki/Ellipse