What Is a Cone?

Daily life presents people with many unexpected geometric forms. One hot summer afternoon outside an ice cream shop on a street corner, an ice cream cone caught the eyes of many passersby because it has such a distinct appearance - not only has this simple but mysterious solid attracted people's interest but it plays an essential part in mathematics, engineering and artistic design as well. This article offers an in-depth introduction to this common yet intricate geometric body by discussing its structure, calculation formula, types, historical anecdotes, and modern technological applications.

Definition and Basic Structure of the Cone

Definition of a Cone  

Cones are solid figures composed of a circular base with a fixed point (the vertex) outside its plane of origin. They are connected by line segments extending out from this vertex and to all points along its circumferential boundary to form its curved surface.

Components

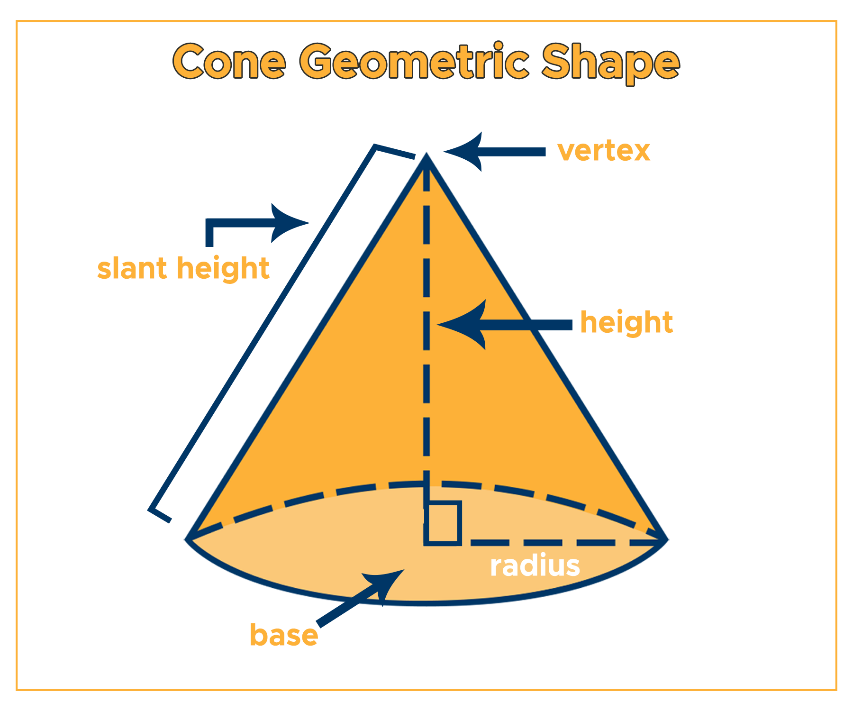
Base, Vertex, and Axis  

A cone's foundation consists of a flat, perfectly circular plane called its base; its vertex stands as an outside point in this plane; from this vertex to its center lies what's known as its "axis", an important reference that defines overall orientation as well as showing characteristic symmetry and providing geometric balance in this particular form of geometry.

Radius, Vertical Height, and Slant Height 

The radius \(r\) of a cone's base determines its overall width and size, setting its lateral extent. Meanwhile, the vertical height \(h\) measures the perpendicular distance from the vertex to the plane that contains the base, providing a precise measure of the cone's elevation. The slant height \(l\) measures the direct distance from the vertex to any point on the edge of the circular base, capturing its inclined dimension.

Types of Cones

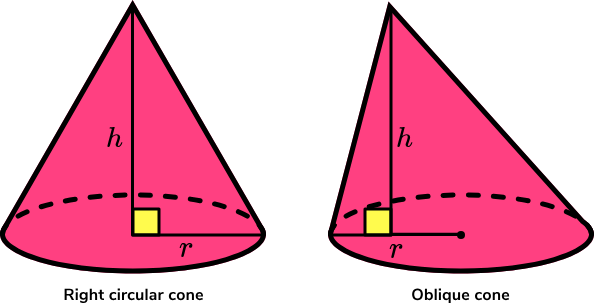
Right Circular Cone  

The right circular cone is one of the most frequently encountered types, characterized by having its vertex precisely aligned above the center of its base circle to achieve perfect rotational symmetry throughout. This feature gives this cone its elegant, upright form while simplifying many mathematical computations; many engineering designs and manufacturing processes prefer using it due to its proven formulae and applications that produce highly stable results.

Oblique Cone  

In contrast with the right circular cone, an oblique cone presents notable geometric variations wherein its vertex does not rest directly above the base, leading to loss of complete rotational symmetry, creating irregular shapes within it and rendering its overall form less regular. Although its dynamic aesthetic benefits from asymmetry, this mathematical complexity adds significant complication to calculations. As non-symmetric cones lack symmetry, properties like surface area, volume, and stress distribution cannot be calculated using formulae specific to right circular cones. Therefore, while oblique cones may be chosen for artistic installations and architectural designs that seek to highlight an unusual or unconventional form, their usage in precision mechanical designs where stability and predictable numerical outcomes are more critical is more limited to projects where creative expression outweighs computational simplicity.

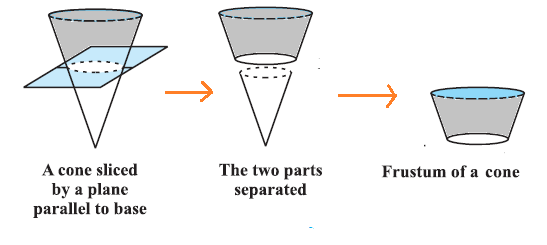
Special Cases: Frustum of a Cone and Bicone  

Frustums of cones can be created by cutting away the top portion of a right circular cone while leaving similar-shaped lower parts intact while taking off portions similar to its top section to form funnel-like structures. This design can be found across industries such as architecture and industry; for instance, water tanks or funnels. A bicone structure appears in certain processing and theoretical models, characterized by two simultaneous vertex presence. Its construction often allows researchers to explore properties like bilateral symmetry or dual folding; though these cases may seem niche-like in comparison with others, their geometric properties and calculation methods hold great meaning for theoretical research.

Formulas and Calculations of the Cone

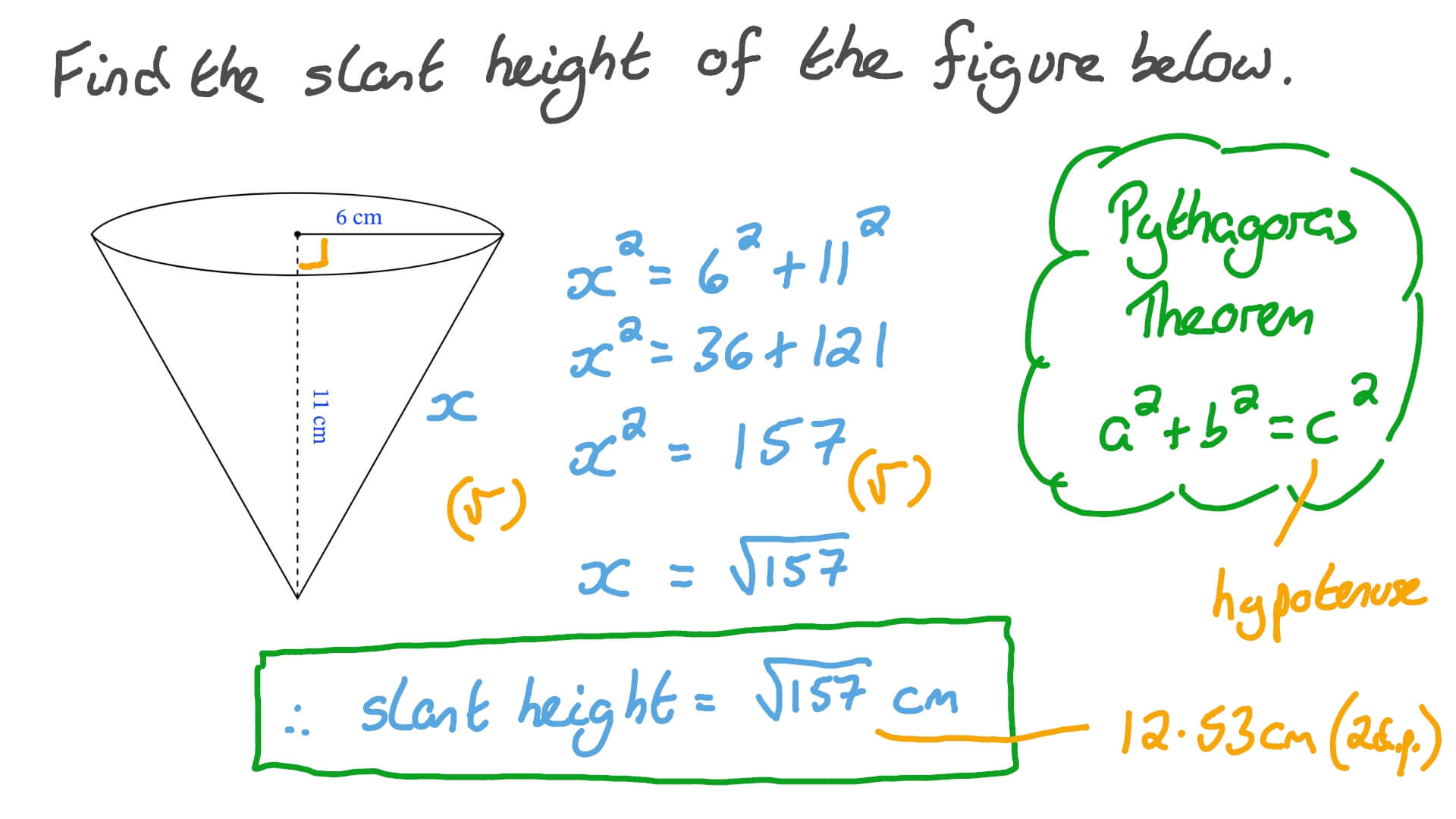
Slant Height Formula  

The slant height (\(l\)) of a cone refers to the straight-line distance from its vertex to any point on its base. Given that its construction comprises vertical height \(h\) and base radius \(r\) as two perpendicular sides of a right triangle, the Pythagorean theorem allows us to calculate this value with specific formulae:

\[l=\sqrt{r^2+h^2}\]

This formula is often utilized in engineering calculations and geometric modeling for cone dimensions determination, providing the primary source for measuring their lateral surfaces.

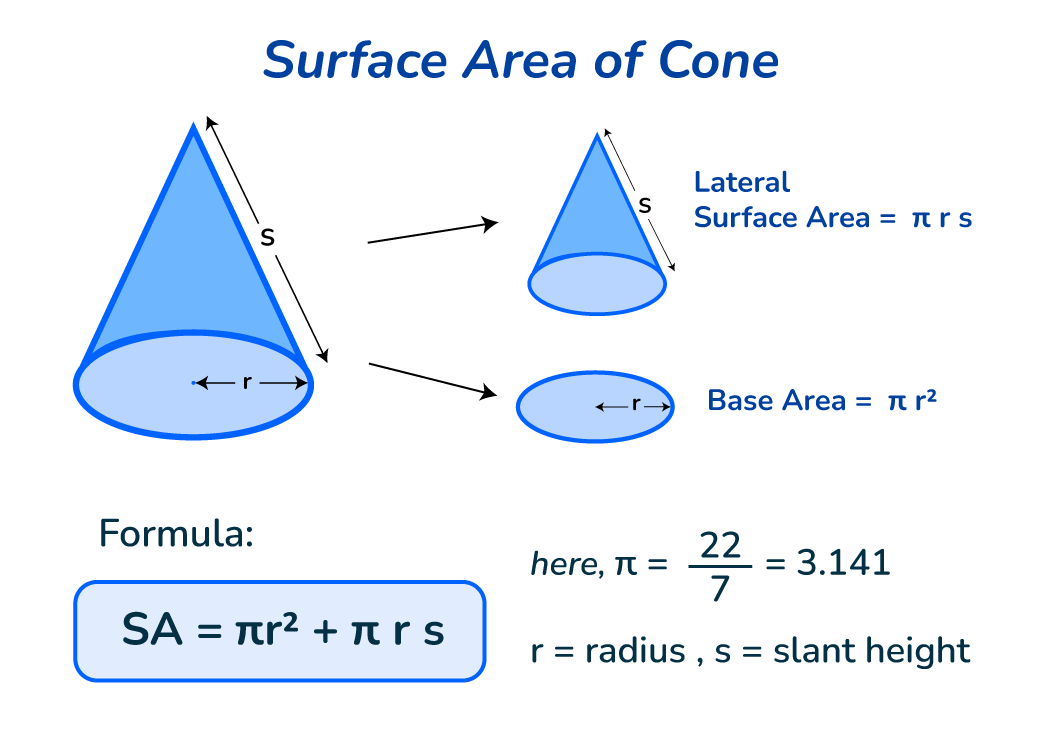
Surface Area Formulas  

Lateral (Curved) Surface Area Formula 

The lateral surface area of a cone refers to the region covered by segments from its vertex to base circumference, calculated with this formula:

\[A_{\text{lateral}}=\pi r l\]

where \(r\) denotes the base radius and \(l\) is the slant height. This formula represents an inherent relationship among lateral surface area, base radius, and height and the relationship of these three variables; hence it may be applied both theoretically and practically when carrying out calculations or measurements.

Total Surface Area (Including Base) Formula  

In typical geometric applications, the total surface area of a cone comprises both its lateral surface area and base area - typically calculated via \(\pi r^2\) calculation; hence its total surface area formula reads as:

\[A_{\text{total}}=\pi r l+\pi r^2\]This formula, which adds the areas of both surfaces and bases, can help estimate material consumption and cost budgeting in engineering design projects.

Volume Formula  

Volume \(V\) calculations for cones depend on their geometric structures. They can be seen as composed of many infinitesimally thin layers that add up over time, leading us to this formula:\[V=\frac{1}{3}\pi r^2 h\]Here, \(r\) is the radius of the circular base while \(h\) is perpendicular height, with coefficient\(\frac{1}{3}\)， signifying that the cone's volume equals one-third that of an equivalent cylindrical volume; This formula has proven invaluable in fluid mechanics, architecture and engineering for precise volume determination and is an indispensable foundation in calculation scenarios.

Differences Between Cones and Other Shapes

Although all three structures - cones, cylinders, and spheres - possess circular elements, their structures and geometric properties exhibit distinct variations. A cone features a circular base and an apex not lying within its plane of the base; its lateral surface can be created by connecting each point along its circumference through connecting to its apex; its volume can then be calculated.

\[V=\frac{1}{3}\pi r^2 h\]

This formula illustrates that the volume of a cone is only one-third that of its equivalent cylinder. By comparison, cylinders feature two congruent circular bases connected by an uninterrupted surface; their volume can then be calculated as follows.

\[V=\pi r^2 h\]

Concerning surface area, measuring the area of a cone requires both its lateral curved surface and base areas; when measuring a cylinder's base areas in addition to side area. When considering volume calculation for spheres however, no measurements need to be made since all their surfaces are curved with no flat base areas present; its volume is simply given by its volume calculation.

\[V=\frac{4}{3}\pi r^3\]

Cones have distinct physical properties when compared to cylinders or spheres in terms of load distribution, light reflection, fluid dynamics, and fluid dynamics that provide different physical benefits for load distribution, light reflection, and fluid dynamics compared to their counterparts; these distinctions not only influence engineering design, manufacturing processes, and structural stability analyses but also inspire diverse artistic forms and visual expressions that demonstrate both their aesthetic value and functional characteristics.

Anecdotes and Historical Origins Related to Cones

Ancient Architectural Innovations and Mathematical Theories  

Mathematicians and artists alike have long found inspiration in exploring the shape of a cone since ancient times. From various cultures all across history to the present day, its fascinating history uncovers secret knowledge, both natural and artistic alike. Ancient Egyptian pyramids, for instance, often take inspiration from conical shapes as their base design element. Ancient Egyptian pyramids stand as a testament to both the architecture and astronomy of their time; moreover, they display their masterful understanding of conical structures' mechanical stability. Designs similar to the frustum of cone designs played an instrumental part in weight reduction while simultaneously increasing aesthetic value; today, these designs remain inspirations in architectural design.

Archimedes of Ancient Greece made waves when his studies revealed subtle relationships in volume calculations between cones and spheres, becoming one of the classic achievements in early geometry. He proposed ingenious formulae for solid volumes like proportional relationships between cone and sphere volumes - setting off subsequent mathematical research efforts. Arab mathematicians later European scholars adopted and refined Archimedes' theories while actively advocating precise methods of computing cone volumes that have since proven invaluable applications across fields including surveying engineering astronomy.

Renaissance Artistic Influence and Modern Architectural Legacy  

Renaissance artists employed conical lines to represent spatial gradients and layers in perspective drawings, which not only enhanced three-dimensional perception but also seamlessly combined geometry with artistic design - becoming an influential source of cross-disciplinary inspiration. Many architectural designs also adopted this geometric form, from church spires to skyscrapers - bearing witness to its rich historical legacy.

A New Perspective on Cones in Modern Technology

Applications in Engineering and Architecture  

Conical structures are widely employed in engineering design and construction due to their excellent load-bearing performance and aesthetic qualities. Modern architecture utilizes conical structures extensively; for instance, towers, bridges, and domes often employ intermediate conical structures, which not only increase overall stability but also create an eye-catching visual impact. By employing the formula shown below, we can effectively achieve both performance and aesthetic qualities simultaneously.

\[V=\frac{1}{3}\pi r^2 h\]By employing scientific material utilization estimation techniques, construction designs become more accurate and reliable.

Inspirations from Nature and Artistic Design  

Natural phenomena, including pine cones, hailstones, and mountain contours that closely resemble conical shapes, have long inspired artists and designers, serving as an endless source of creativity in various fields such as sculpture, installation art, and industrial product design. Artists use its inherent geometric beauty as a catalyst to ignite artistic passion within various fields: from sculpture and installation art installations to industrial product design - artists utilize its subtle proportions not only as aesthetic features of works created but also cleverly integrated within works for an aesthetic effect that showcases both rational geometry and artistic sensibility within works demonstrating perfect union between rational geometry and artistic sensibility within works!

Digital Modeling and Simulation Experiments  

With the advancement of computer-aided design technology, digital modeling and simulation experiments have become effective tools for studying conical structures. Utilizing fundamental mathematical relationships, such as those found in formulae, will enhance these studies further.

\[l=\sqrt{r^2+h^2}\]Engineers can utilize digital tools such as these for accurate stress analysis of cone structures in virtual reality environments, optimizing structural designs while increasing experimental precision. Utilizing such digital tools not only reduces testing cycles but also leads to continuous advancements in both engineering and scientific research.

This article presents an in-depth examination of cone structure, formulae, and types, with extensive explanations covering its historical roots to modern applications in engineering, architecture, and natural art, as well as digital modeling applications. Cones have become popular architectural elements; in natural art, their form provides inspiration while digital modeling enables precise replication; all this makes this content vivid and lively, showing mathematics' perfect harmony with practice!

reference:

https://en.wikipedia.org/wiki/Cone

https://en.wikipedia.org/wiki/Pythagorean_theorem

https://en.wikipedia.org/wiki/Sphere