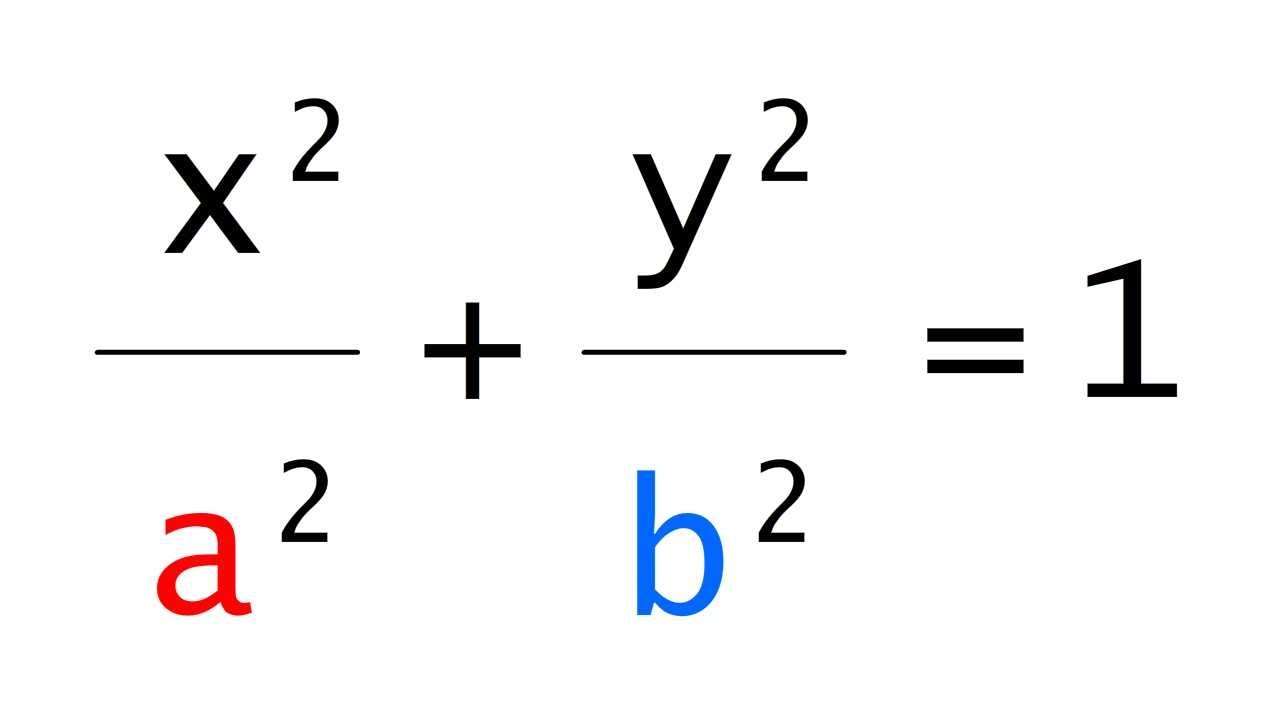What Is an Ellipse?

Mathematics plays an integral part in everyday life; it plays an integral part in explaining natural phenomena. One such natural event that requires mathematics to explain is the shadow of circular objects, whereby when a light source tilts slightly away, its shadow transforms from circularity into something entirely unique—an ellipse. Not only are ellipses ubiquitously found throughout art and architecture, but they play an essential part in both astronomy and physics, too! Let us delve further into understanding these mysterious yet ubiquitous geometric figures through this article.

Definition and Basic Characteristics of an Ellipse

Definition of Ellipse

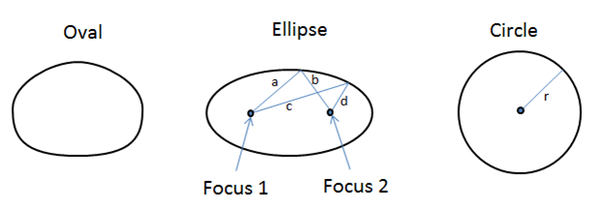
An ellipse is a geometric figure defined by its constant distances from any point on its curve to two fixed points known as its foci (Foci). Simply put, it consists of all points in the plane that satisfy this unique condition.

Mathematically, an ellipse can be defined as follows: Given two fixed points \(F_1\) and \(F_2\) on a plane, any point \(P\) satisfies the condition:

\(|PF_1| + |PF_2| = 2a \quad (a > |F_1 F_2|/2),\)

where the path traced by \(P\) is an ellipse.

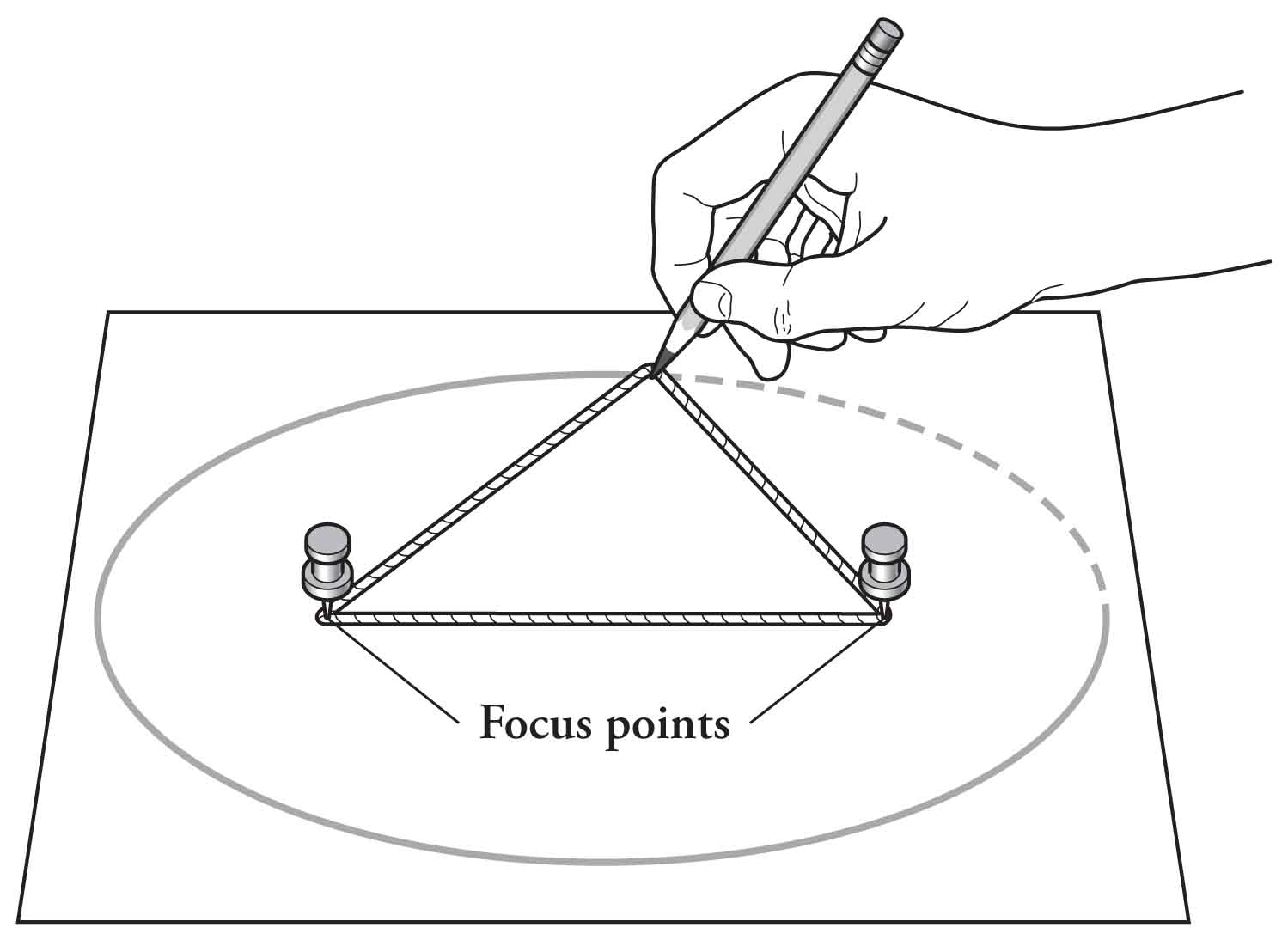
Formation of an Ellipse

An ellipse can be formed using various means. One popular technique involves fixing both ends of a fixed-length string to the foci of an ellipse's focal points, and pulling taut with a pencil leads to creating the constant-distance property: An ellipse is revealed.

\(|PF_1| + |PF_2| = 2a\)

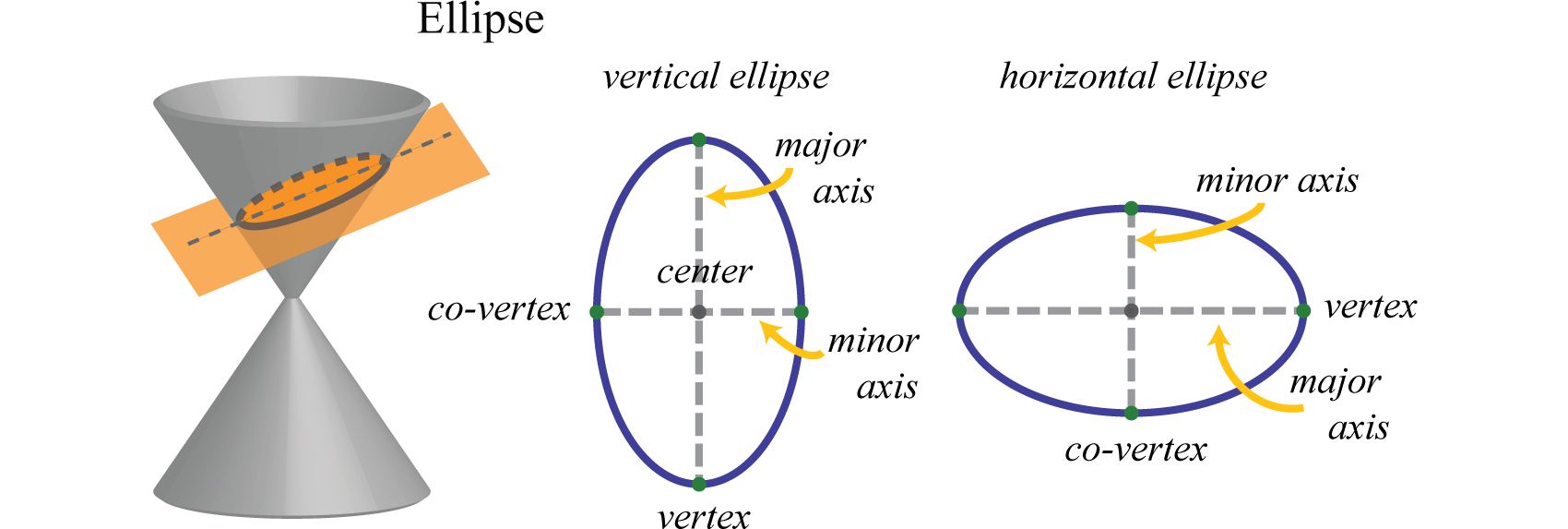
An ellipse in analytic geometry is determined by its intersection between a cone and inclined plane at an angle less steep than their respective cone slant heights, leading to its classification as a type of "conic section."

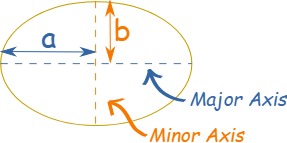
Shape and Symmetry of an Ellipse

An ellipse's shape can be described by its major and minor axes:

- The major axis defines the longest line segment through an ellipse with an approximate length of two times a radius (2a).

-- The minor axis lies perpendicular to the major axis and represents the shortest line segment through an ellipse with an edge length of ( 2b ).

An ellipse exhibits bilateral symmetry; its center serves as its symmetry point.

- Ellipses are geometric figures characterized by being symmetric about both major and minor axes, creating a balance in its geometric form that emphasizes perfect equilibrium.

Horizontal and Vertical Ellipses

Ellipses can be divided into two classes according to their major axis direction:

1. Horizontal Ellipse (Major Axis along \(x\)-axis):  

\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \quad (a > b > 0)\)

2. Vertical Ellipse (Major Axis along \(y\)-axis):  

\(\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1, \quad (a > b > 0)\)

Even when its direction varies, its fundamental geometric properties remain identical.

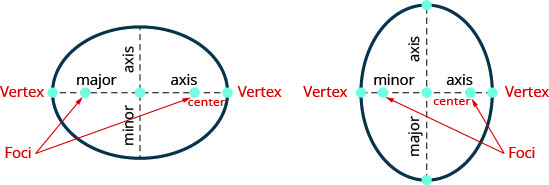
Components of an Ellipse

Foci

Foci are among the most critical elements of an ellipse. Given that an ellipse with major and minor axis lengths of 2a and 2b, respectively, is shaped as follows, its distance between foci can be expressed as follows.

\(c = \sqrt{a^2 - b^2}, \quad (a > b).\)

The coordinates of the two foci \(F_1\) and \(F_2\)are:  

- For a horizontal ellipse: \(F_1(-c, 0)\) and \(F_2(c, 0)\).  

- For a vertical ellipse: \(F_1(0, -c)\) and\(F_2(0, c)\).  

The foci determine the overall shape and geometry of an ellipse by adhering to its key property:

\(|PF_1| + |PF_2| = 2a,\)

Where \(P\) is any point on the ellipse.

Center

The center marks the intersection point between major and minor axes and serves as the symmetry center of an ellipse. When working with simplified standard form equations in analytic geometry, however, the center acts as a reference point - such as when solving standard form equations using simplified standard form forms of standard equations.

- For horizontal ellipses, the center coordinates are either \((0, 0)\) or \((h,k)\) if offset from their original locations (the origin).

This tool assists with deriving and calculating parameters of horizontal ellipses.

Vertices and Directrix

- Vertices: These are the endpoints of the major axis.  

- For a horizontal ellipse: \((a, 0)\) and \((-a, 0)\).  

- For a vertical ellipse: \((0, a)\) and \((0, -a)\).  

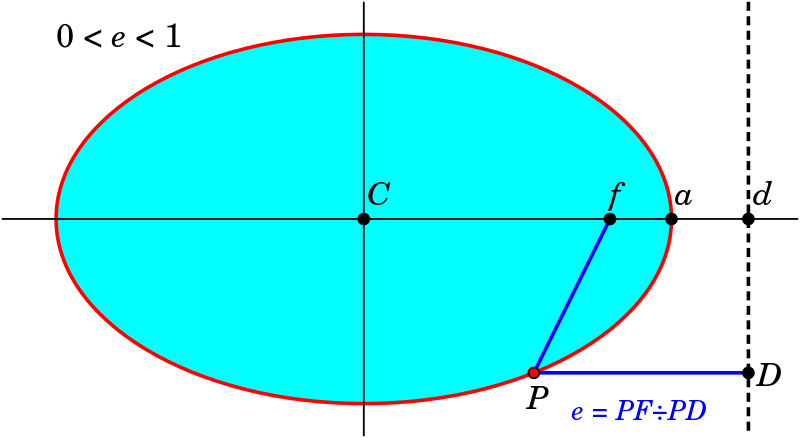
- Directrix: A directrix is an auxiliary line related to the focus that defines its relationship to an ellipse:

- For a horizontal ellipse:  

\(x = \pm \frac{a}{e}, \quad e = \frac{c}{a}.\)

- For a vertical ellipse:  

\(y = \pm \frac{a}{e}, \quad e = \frac{c}{a}.\)

Here, \(e\) represents the eccentricity of the ellipse.

Major and Minor Axes

The major axis of an ellipse is defined as its longest diameter between both foci.

\(\text{Length of Major Axis} = 2a.\)

Conversely, the minor axis is the shortest diameter, perpendicular to the major axis:  

\(\text{Length of Minor Axis} = 2b.\)

Transverse and Conjugate Axis

- The transverse axis refers to the major axis, emphasizing the symmetry and structure of an ellipse.

The conjugate axis refers to its shorter minor axis for better geometric understanding of an ellipse.

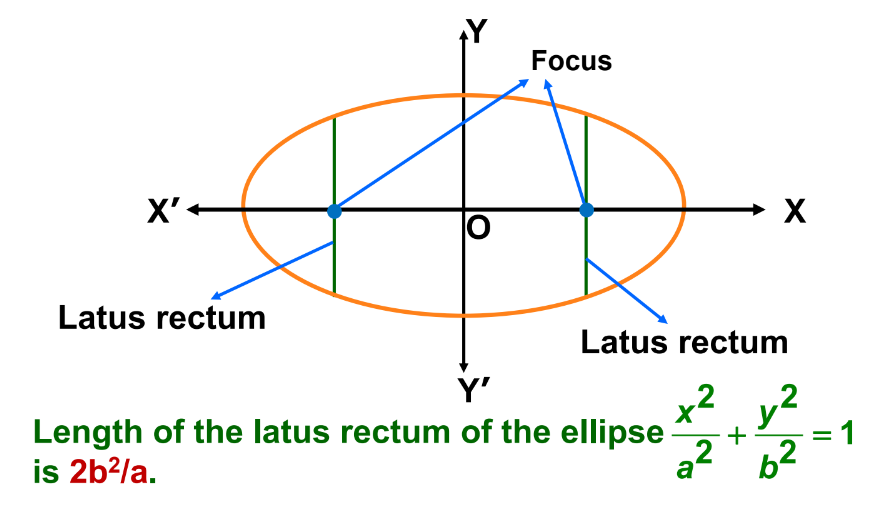
Latus Rectum

A "latus rectum" (line segment perpendicular to the major axis and passing through a focus) is defined by:

\(\text{Length of Latus Rectum} = \frac{2b^2}{a}.\)

This property is especially essential in optical and geometric analyses.

Equations of Ellipse and Derivation

Standard Form of Ellipse Equation

The standard form of an ellipse equation provides the means of describing its geometric properties. Depending on which direction its major axis points in, two forms exist for this equation:

1. Horizontal Ellipse (Major Axis along \(x\)-axis)  

\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \quad (a > b > 0)\)

Here:  

- \(a\): Semi-major axis (parallel to the \(x\)-axis);  

- \(b\): Semi-minor axis (parallel to the \(y\)-axis);  

- \(c = \sqrt{a^2 - b^2}\): Distance from the center to each focus;  

- Foci: \((-c, 0)\) and \((c, 0)\).  

2. Vertical Ellipse (Major Axis along \(y\)-axis)  

\(\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1, \quad (a > b > 0)\)

Here:  

- \(a\): Semi-major axis (parallel to the \(y\)-axis);  

- \(b\): Semi-minor axis (parallel to the \(x\)-axis);  

- \(c = \sqrt{a^2 - b^2}\): Distance from the center to each focus;  

- Foci: \((0, -c)\) and \((0, c)\).

General Form Equation

A standard form for an ellipse equation can be generalized into this form:

\(Ax^2 + By^2 + Cx + Dy + E = 0, \quad (A > 0, B > 0),\)

Where the constants A, B, C, D, and E are constants, this general form can be reduced to standard form through transformations such as completing the square.

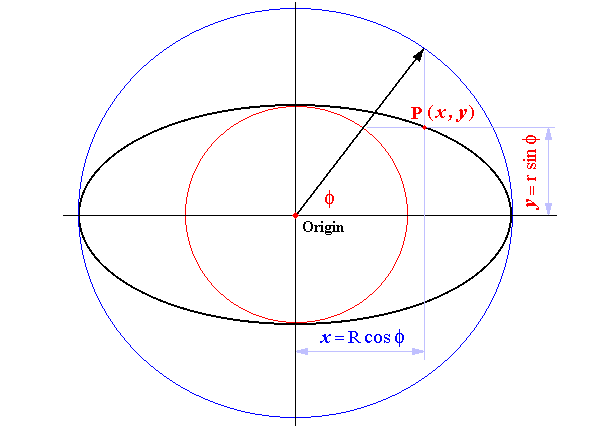
Parametric Equation

Parametric equations offer another method for representing an ellipse: they offer dynamic representations. An example would be an ellipse with its center at (0, 0); this would yield:

1. Horizontal Ellipse:

\(x = a \cos\theta, \quad y = b \sin\theta, \quad \theta \in [0, 2\pi]\)

2. Vertical Ellipse:

\(x = b \cos\theta, \quad y = a \sin\theta, \quad \theta \in [0, 2\pi]\)

Here, \(\theta\) represents the angle between the line connecting \(P(x, y)\) to the center of the ellipse and the positive \(x\)-axis of the ellipse. This parametrization can be especially helpful in plotting or dynamically computing points on the surface of an ellipse.

The Derivation of Ellipse Equation

The derivation of an ellipse equation follows from its geometric definition: the sum of distances from any point on the curve to both foci is constant. Here is how:

1. Given that the foci of an ellipse are at \((-c, 0)\) and \((c, 0)\), any point \(P(x, y)\) on it must satisfy:

\(|PF_1| + |PF_2| = 2a.\)

2. Expand the distance terms:

\(\sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a.\)

3. Square both sides and simplify using algebra, yielding:

\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \quad \text{where } b^2 = a^2 - c^2.\)

This confirms the standard form of an ellipse equation applicable to both horizontal and vertical ellipses.

Properties of an Ellipse

Eccentricity of Ellipse

Eccentricity (abbreviated "\(e\)") is a numerical measure of an ellipse's shape that quantifies it by taking the ratio between the distance between foci to the length of the major axis. This value determines eccentricity \(e\).

\(e = \frac{c}{a}, \quad (0 < e < 1),\)

where \(c = \sqrt{a^2 - b^2}\).  

At \(e \to 0\), an ellipse approximates a perfect circle; at \(e \to 1\), its dimensions become more stretched out.

Constant Sum of Distances to Foci

An important characteristic of an ellipse is that its sum of distances from any point\(P\) on it to both foci \(F_1\) and \(F_2\)remain constant and equal \(2a\):

\(|PF_1| + |PF_2| = 2a.\)

Optics relies heavily on this property, as its explanation lies within elliptical mirrors and lenses' ability to focus.

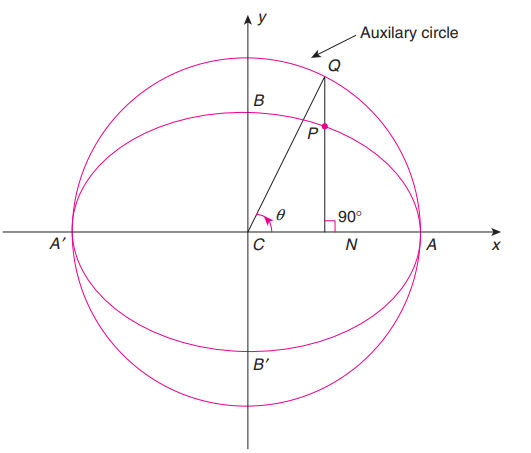
Auxiliary Circle

An auxiliary circle for an ellipse is defined as any circle centered at its center with radius equal to semimajor axis \(a\):

\(x^2 + y^2 = a^2.\)

An auxiliary circle helps in parameterizing an ellipse and studying its geometric properties.

Director Circle

The director circle is a theoretical concept used in advanced geometry. It refers to the locus of points from which tangents drawn to an ellipse are perpendicular to its focal axis and has an equation:

\(x^2 + y^2 = a^2 + b^2.\)

This circle draws attention to the relationship between ellipse and circular symmetry and has applications in optical system designs.

Applications of an Ellipse

Applications in Physics and Engineering

Ellipses play an integral role in several disciplines of physics and engineering. Some key applications of this shape include:

1. Optics Design: Ellipses exhibit a unique reflective property, whereby any light ray emanating from one focus reflects off the inner surface of the ellipse and converges at the second focus. This property is crucial in the design of elliptical reflectors, optical concentrators, and acoustic devices.  

For instance, in an elliptical mirror, a light source placed at one focus directs all reflected rays to converge perfectly at the other focus, enabling precise light or energy concentration.

2.Bridge and Dome Structures: Both ancient and modern bridges and domes employ elliptical designs in order to distribute load efficiently, which leads to enhanced stability when under pressure.

Examples include St Paul's Cathedral in London and Roman amphitheaters that utilize elliptical arches.

3. Orbital and Particle Motion: Elliptic trajectories often result from studying particle motions and orbits in physics.

Charged particles moving through a uniform magnetic field may take an elliptical trajectory in certain circumstances.

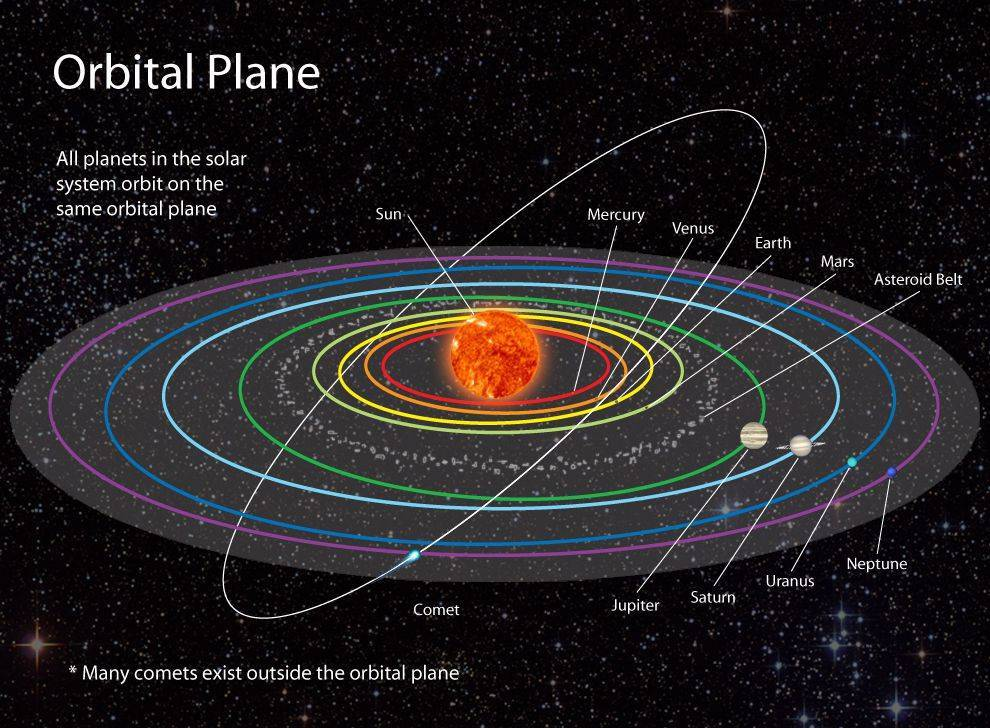
Significance in Astronomy

Ellipses play an integral part in astronomy, perhaps best expressed by Kepler's First Law of Planetary Motion, which states:

A planet's orbit around the Sun can be represented as an ellipse with one focus as its centre point;

Specific applications for Planetary Orbits include:

1. Planetary Orbits: The orbits of Earth, Mars, and other planets around the Sun can be approximated using an ellipse model; however, their eccentricities \(e\) tend to be quite low, which means their paths are often nearly circular in form.

For example, Earth's orbit features an eccentricity of approximately 0.0167, making its path nearly circular.

2. Comet Trajectories: Comet trajectories are very different from planet trajectories in that their eccentricities tend to be significantly greater—often approaching 1. Their orbits follow highly elongated ellipses with eccentricities approaching one.

Halley's Comet, for instance, follows an elliptical orbit.

3. Binary Star Systems: These binary star systems feature two stars orbiting around their common center of mass in an elliptical manner - understanding this feature is key when studying astrophysical dynamics.

Real-World Examples

Ellipses can be found everywhere in everyday life and serve a number of practical uses:

1. Athletic Tracks: Standard running tracks resemble an elliptical shape by having two straight sections connected by semicircles to approximate its shape aesthetically while meeting functional efficiency needs. This structure ensures aesthetic balance while optimizing functional efficiency.

2. Elliptical Trainers: These exercise machines employ motions similar to an elliptical trajectory to minimize impact on joints while offering natural stride options that create effective cardiovascular workouts.

3. Art and Architecture: Ellipses are common in garden layouts, sculptures, and decorative designs due to their symmetrical forms and visual appeal. Lakes or fountains in landscape architecture sometimes adopt an elliptical shape for aesthetic harmony.

Ellipse Formulas

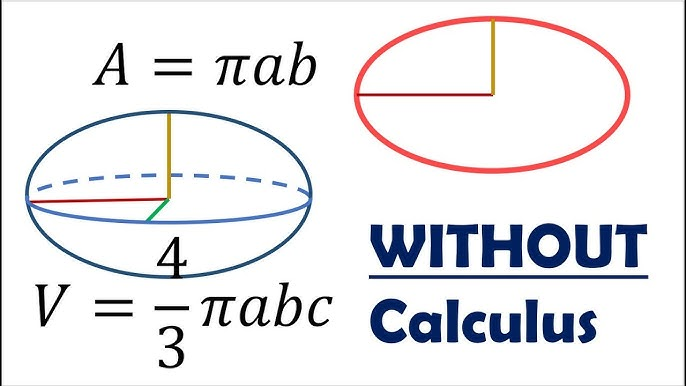
Area Formula

An ellipse's area can be calculated using its semi-major and semi-minor axes; its formula follows.

\(\text{Area} = \pi \cdot a \cdot b,\)

Where:

- \(a\): Semi-major axis length,  

- \(b\): Semi-minor axis length,  

- \(\pi\): The mathematical constant is approximately 3.14159.

This formula may be obtained either via integration or by comparing an ellipse's proportions with those of a circle.

Perimeter Formula

An approximate formula known as Ramanujan's first approximation can often provide the solution:

\(\text{Perimeter} \approx \pi \cdot \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right].\)

For exact calculations, one can use an elliptic integral:

\(\text{Perimeter} = 4a \cdot \int_{0}^{\frac{\pi}{2}} \sqrt{1 - e^2 \sin^2\theta} \, d\theta,\)

where \(e = \frac{c}{a}\) is the eccentricity of the ellipse.

Latus Rectum Formula

The length of the latus rectum is an essential property of an ellipse, especially in its reflective and optical applications. The formula is:

\(\text{Length of Latus Rectum} = \frac{2b^2}{a}.\)

This measurement is crucial in studying elliptical orbits and optical paths.

Tangent and Normal Equations

The length of the latus rectum is an integral property of an ellipse, and its reflective and optical applications include reflection. To find its formula:

1. Tangent Equation:

- For a horizontal ellipse:

\(\frac{xx_1}{a^2} + \frac{yy_1}{b^2} = 1.\)

- For a vertical ellipse:

\(\frac{xx_1}{b^2} + \frac{yy_1}{a^2} = 1.\)

2.Normal Equation (Perpendicular to Tangent): For normal lines, slope equals the reciprocal negative of their tangent slope; this expression can also be written using a derivative of an ellipse's equation as input.

These equations establish a geometric relationship between points on an ellipse and its adjacent lines.

Comparative Analysis of Ellipse and Other Geometric Shapes

Differences Between an Ellipse and a Circle

An ellipse and circle differ primarily in their focal properties:

1. A circle can be thought of as being an extreme case of an ellipse in which both foci converge at one single point (called its center).

2. In an ellipse, \(a > b\), whereas for a circle \(a = b = r\) (radius).  

- Ellipse equation:  

\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.\)

- Circle equation:  

\(x^2 + y^2 = r^2.\)

Overall, circles demonstrate higher symmetry and the eccentricity \(e = 0\).

Relation Between an Ellipse and an Oval

An ellipse is a mathematically rigorous shape; an oval refers more broadly to any round and elongated figure with round contours that approximate an ellipse's perimeter; some ovals approximate this property but fail to satisfy constant-sum distances to foci properties.

Comparison Between Ellipse and Hyperbola

Ellipses and hyperbolas both share similarities as conic sections with two foci; however, their properties vary considerably:

1. Definitions:

- Ellipse: The sum of distances to two foci is constant.

\(|PF_1| + |PF_2| = 2a.\)

- Hyperbola: The difference of distances to two foci is constant.

\(|PF_1| - |PF_2| = 2a.\)

2. Shape: An ellipse is defined as a closed curve while hyperbolas are open curves with two branches, providing distinct applications within both physics and geometry.

As an essential geometric figure, an ellipse symbolizes both mathematical elegance and practical utility. From planetary motion in astronomy to engineering precision in optics and structures, its applications span diverse fields. We investigated definition, components, equations properties properties as well as real life relevance of ellipses for this article. With its mix of theoretical significance and tangible reality implications, it stands as a cornerstone of geometry as a connection between abstract mathematics and tangible reality.

reference:

https://en.wikipedia.org/wiki/Ellipse

https://en.wikipedia.org/wiki/Hyperbola

https://en.wikipedia.org/wiki/Director_circle