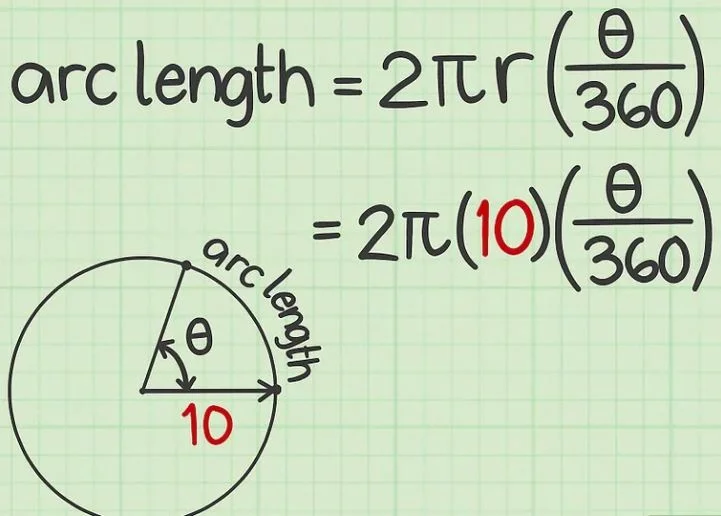What Is a Circle?

Everyday we come into contact with circles - an inconspicuous yet profound geometric shape. From learning how to draw one as children through exploring its properties in math classes, the circle has long been part of our understanding of our universe. From wheels and clocks to dinner plates - circles exist everywhere we look! However, behind this seemingly simple shape are centuries of history, profound mathematical principles, and numerous practical applications; we will use this article as an opportunity to unravel this essential geometric concept further!

Basic Concept and Definition of a Circle

At its core, circles can be understood as sets of points on a plane that are evenly spaced from a fixed point called its center - although seemingly straightforward at first glance, this definition has far-reaching ramifications in both mathematical theory and real life applications.

What Is a Circle?

A circle is a special type of curve found in geometry with no beginning and no endpoint. Its intuitive meaning lies in being composed of all points equidistant from one central point; distance from center to any point on circle known as radius, another key characteristic being equal length radii on all circles in which they exist.

Mathematically speaking, circles play an integral part of mathematics: as foundation for fields like analytic geometry and pure mathematics as well as myriad real-life issues and solutions. Understanding their definition is therefore vital in order to explore further into their properties and applications.

Historical Development of Circles

The circle is not only one of the fundamental concepts in geometry but it is also at the core of humanity's quest to understand nature and science.

The Origin and Early Applications of Circles

Circles in Ancient Cultures

Early humans held the circle as an essential tool in both cultural and scientific explorations, such as those conducted by ancient Egyptians and Babylonians. For example, ancient Egyptians and Babylonians utilized circles extensively when designing religious artifacts or describing celestial movements, with Babylonian cuneiform records detailing division of circles while Egypt utilized circles extensively during solar worship rituals or architectural designs meant to honor Ra or other deities.

The Role of Circles in Astronomy and Agriculture

Astronomy was among the earliest practical uses for circles, with ancient civilizations like the Mayans and Chinese using circular observations to study celestial bodies and calculate time. Furthermore, they played a critical role in designing irrigation systems and recording agricultural calendars, which helped ancient societies optimize planting and harvesting practices.

Mathematical Representation of Circles

The Circle in Ancient Greek Geometry

Euclid gave an exhaustive description of the fundamental properties of circles in his Elements in ancient Greece, providing precise definitions and exploring various geometric relationships like tangents, inscribed shapes, and circumferences. His work laid the groundwork for further geometric studies.

Archimedes’ Contributions to Circle Area and Perimeter Calculations

Archimedes revolutionized our understanding of circles by probing their area and perimeter. His discoveries provided methods of approximating circle areas by approximating pi (\(\pi\)). His breakthrough discoveries are unparalleled by any other mathematical thinkers during that era; today, they form the basis of the mathematical understanding of circles.

Ancient Chinese Research on Circles

Ancient Chinese mathematicians such as Liu Hui developed their own techniques for investigating circles. Utilizing "cutting the circle", Liu Hui accurately calculated pi's value and advanced geometry's development significantly in East.

Modern Development and Applications of Circles

The Formalization of Circles in Analytic Geometry

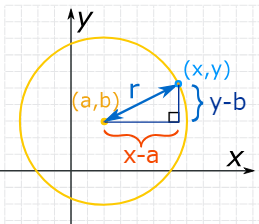
Rene Descartes' development of the coordinate system enabled circles to be represented precisely and analyticly; his standard equation for circles provided this possibility.

\((x-h)^2 + (y-k)^2 = r^2\)

Analyzing and depicting circles' geometric properties becomes easier.

Applications of Circle Theory in Physics, Engineering, and Intelligent Technologies

Today's theories of circles go well beyond pure mathematics; they can also be found in fields as disparate as physics engineering and intelligent technology. Circular designs predominate mechanical systems like gears; circular motion is fundamental in physics; while artificial intelligence algorithms employing circle theory have applications like pattern recognition and image analysis.

Components of a Circle

Understanding a circle's construction entails unwrapping its various geometric parts, essential to understanding its properties and uses.

Circumference  

Circumference refers to the total length around any circle and is one of its core dimensions. To calculate its circumference, one formula could be:

\(C = 2 \pi r\)

where \(r\) is radius and \(C\) is circumference.

Radius  

A radius measures the distance from any point on a circle's circumference back to its center point and thus defines its size; all radius values within any single circle will always remain equal.

Diameter  

The diameter is the longest chord within any circle. It runs through its center and links two points on either side; its length equaling twice that of its radius:

\(d = 2r\)

This makes it the ideal measure to determine where its edges begin and end on any given circle.

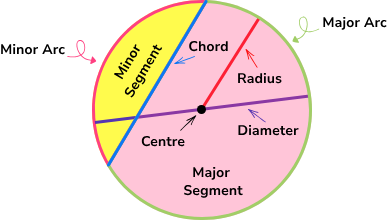
Chord  

Chord is any line segment connecting two points on a circle without necessarily passing through its center.

Arc  

An arc is defined as any portion of a circular path between two points that connect them, classified either as minor arc or major arc depending on its length.

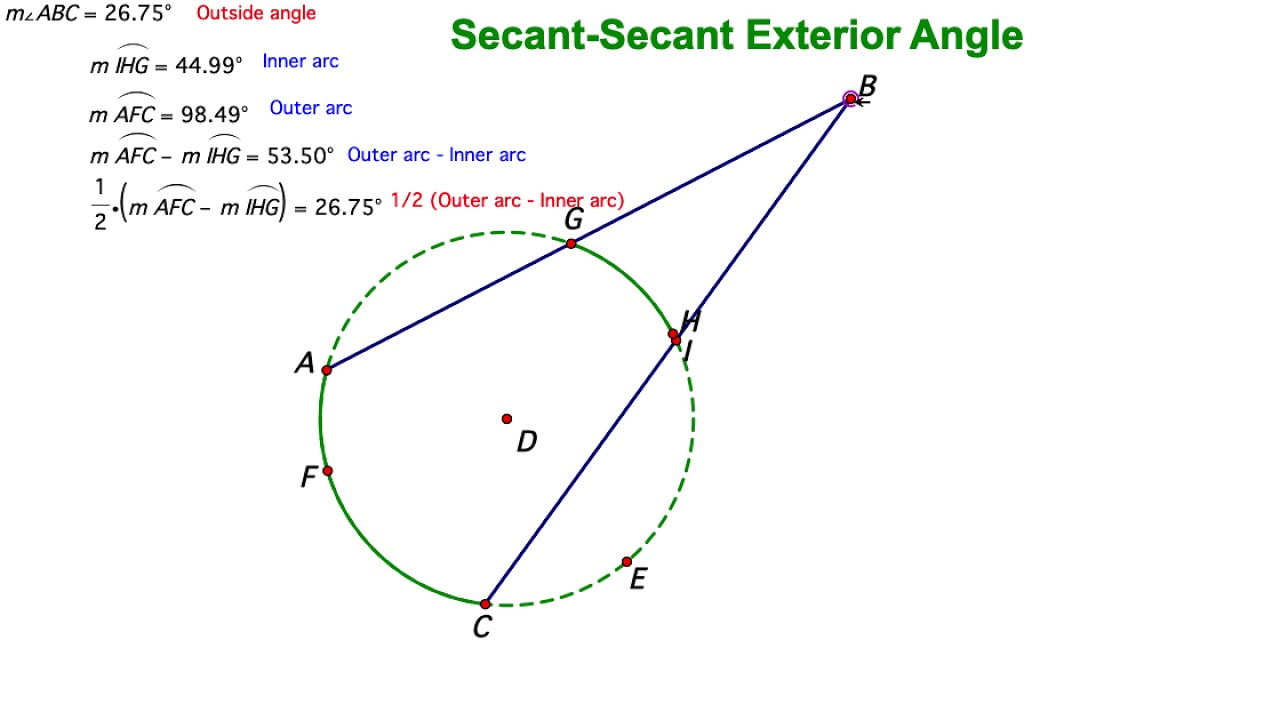
Secant  

A secant is defined as a line which intersects two points on the circumference of a circle, subdividing its interior into two distinct portions.

Tangent  

Tangents are lines that touch a circle at precisely one point and run perpendicular to its radius at that contact point.

Sector  

Sector is defined as an area enclosed by two radii and their intersected arc, creating what resembles "a slice of pizza." Its area corresponds directly with its central angle formation.

Segment  

Segments are areas within a circle bounded by chords and their associated arches; unlike sectors, however, segments do not include the center. Instead they divide its area into two parts: major (larger area) and minor segments (smaller area), depending on the length of chord and arche. They are commonly employed when solving geometry problems involving areas, chords and arches.

These fundamental components provide a detailed framework for studying the structure of a circle. Not only do they describe its geometric form, but they're also key parameters when calculating more complicated attributes like area or circumference.

Basic Properties of a Circle  

As one of the essential geometric figures, circles possess numerous unique properties which contribute both to theoretical research and real world applications.

Geometric Properties of a Circle  

1. Features of Plane Geometry: A circle is an open curve on a plane without beginning or endpoint.

2. Equidistance Property: The circle can also be defined as all points that are equally far away from a fixed point (the center).

3. Maximum Symmetry: When compared with polygons, circles offer maximum symmetry from all directions.

Symmetry of a Circle  

The circle exhibits high degrees of symmetry, making it one of the ideal figures in geometry.

1. Rotational Symmetry: Any rotation of its center around any axis would maintain the original form and maintain shape symmetry without changing in form at all.

2. Axial Symmetry: Any line tracing its way around a circle serves as the axis of symmetry.

Properties Related to Angles  

Angle properties play an essential part in circle geometry, particularly when dealing with arcs and circular segments.

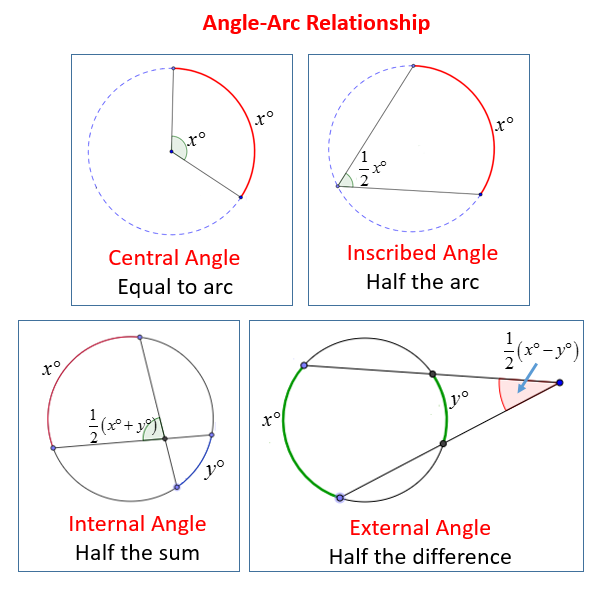
Central Angle  

Central angles are formed when two radii extend from the center outward and meet at two points along the circumference, meeting at points on opposite radii. Their size depends on how much of an arc's fraction of a circle multiplied by 360 degrees it covers.

Inscribed Angle  

An inscribed angle occurs when its vertex lies on the circle's circumference, it is subtended by a chord or arc, and its measure is equal to half of the corresponding central angle - a fundamental property of circles.

Circumference Angle  

Circumference angles are created when two intersecting chords intersect on the circle's circumference and their vertex falls on its circumference. They are closely related to inscribed angles, with equal values for the same arc or equal arcs corresponding to equal circumference angles.

Perpendicular Property of Radius and Chord  

In a circle, if a radius is perpendicular to a chord, it bisects the chord. This property is particularly useful in proving numerous geometric theorems related to special triangles in a circle.

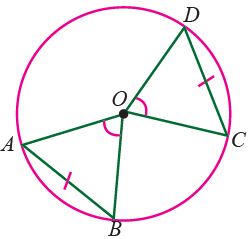
Property of Equal Chords in the Same Circle  

On a circle, chords of equal length subtend equal central angles and circumference angles; similarly, when two central or circumference angles are equivalent, their chords will also be equivalent. This property is critical when studying its symmetry.

These core properties provide an in-depth knowledge of a circle's geometric properties and relationships, making it one of the most versatile concepts in mathematics.

Formulas and Calculation Methods for a Circle

Utilizing various formulas when studying circles provides both theoretical support and practical tools for solving problems more easily, including areas, circumferences and related geometric parameters such as areas or diameters. These formulas enable us to quickly calculate them.

Area Formula  

The area of a circle, as a key indicator of its size, can be determined using this formula:

\(A = \pi r^2\)

where \(A\) represents the area and \(r\) represents the radius. This equation shows that the area of a circle is the product of the square of its radius and \(\pi\).

Circumference Formula  

Circumference (the length around a circle) is defined by this formula:

\(C = 2 \pi r\)

Where C represents circumference and R stands for radius. This illustrates their proportional relationship.

Arc Length Formula  

An arc is defined as any segment of a circle's circumference that can be calculated using:

\(l = \frac{\theta}{360^\circ} \times 2 \pi r\)

where \(l\) is the arc length, \(\theta\) is the central angle subtended by the arc, and \(r\) is the radius.

Sector Area Formula  

Area of a circular sector depends upon its central angle; using that as an index number the formula becomes:

\(A_s = \frac{\theta}{360^\circ} \times \pi r^2\)

where \(A_s\) is the sector area, \(\theta\) is the central angle, and \(r\) is the radius.

Segment Area Calculation Formula  

An area for a circular segment consisting of chord and its associated arc can be calculated as:

\(A_{\text{segment}} = A_s - A_{\triangle}\)

Where \(A_s\) is the area of a sector and \(A_{\triangle}\) is its area formed from two radii and the chord. Calculation of triangle areas depends upon each problem's specific requirements; trigonometric functions can help with that calculation process.

Chord Length Formula  

A chord is defined as any line segment joining two points on a circle and its length can be determined using the following:

\(c = 2r \sin\left(\frac{\theta}{2}\right)\)

These formulas significantly streamline our ability to manage geometric problems involving circles. By representing chord length as \(c\), the central angle subtended by chord as \(\theta\), and radius as \(r\), these formulas make solving theoretical and engineering issues associated with circles much simpler for us.

The Relationship Between Circles and Other Geometric Shapes  

A circle's inherent properties of symmetry and simplicity, combined with its relationships to other geometric forms, enrich theoretical research and provide extensive applications in practical fields.

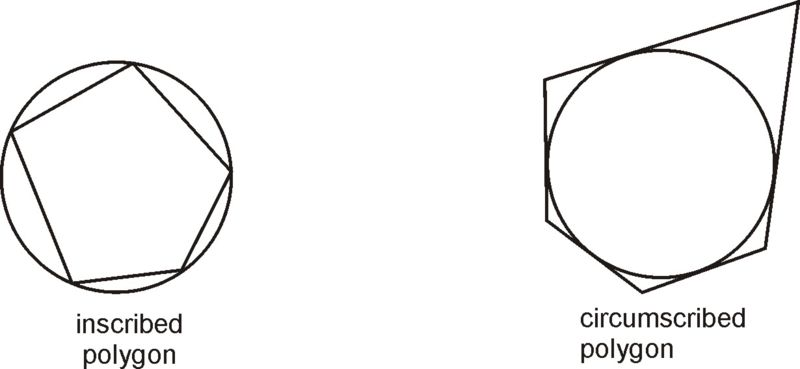
Inscribed and Circumscribed Shapes of a Circle  

Inscribed Shapes  

An inscribed circle may be drawn within a polygon so that its circumference tangent to all sides, as in regular polygons like equilateral triangles and squares where this effect can be observed. The center of an inscribed circle often lies at its geometric center. Its radius ( r ) can also be calculated based on information such as side length or internal angles to generate accurate calculations for inscribed circles within regular polygons like these.  

Circumscribed Shapes  

A circle can enclose any polygon such that its vertices lie within its circumference, creating the circumcircle of that polygon. Any triangle can have its own specific circumcircle, with its center located at the intersection point between perpendicular bisectors of its sides and perpendicular bisectors of perpendicular bisectors of those sides, its radius (R) being mathematically linked to these measurements.

The Intersection of Circles and Polygons  

Circle Division into Polygons  

By subdividing a circle into equal portions, it can be divided further to form various polygons. Dividing it into 3, 4, or 5 parts creates the vertices for an equilateral triangle, square, and regular pentagon, respectively—with more sides representing closer approximations to the circle shape.

Comparing the Area of Polygons and Circles  

As more sides are added to a polygon inscribed within or circumscribing a circle, its area gradually approaches that of the circle itself - this relationship being central to Liu Hui's "cutting the circle" method for approximating \(\pi\).  

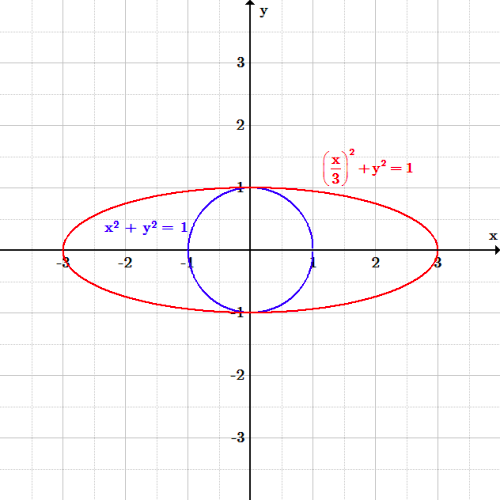
The Relationship Between Circles and Ellipses  

From an abstract point of view, circles are unique forms of ellipses; specifically, when two foci of an ellipse coincide, they become circular, highlighting how closely related circles and other kinds of curves are.

Circles in Spatial Geometry  

Circles form the base for building three-dimensional space spheres; every plane cross section containing circles serves as its cornerstone; calculations used to compute volume and surface area rely heavily upon circular geometric formulas.

Overall, the circle serves both as an iconic two-dimensional shape and as an intermediary for comprehending relationships among various geometric figures. Both its theoretical analysis and practical applications illustrate its relevance within geometry.

The circle as a geometric figure has taken many paths throughout history, from its initial observations and applications through early research applications to today. We explored its roots as well as its composition, fundamental properties, essential formulae, relationships with other shapes, and ultimate manifestations in natural laws. Through this article we looked into its origin, components, fundamental properties, essential formulae and relationships to other shapes. It serves not only as visual symbolism for perfection and balance but is an indispensable element in human thought and creativity - its lasting relevance being an embodiment of these laws manifest themselves through simple forms that come closer than ever to natural laws themselves - just what the circle represents both visually.

reference:

https://en.wikipedia.org/wiki/Circle

https://en.wikipedia.org/wiki/Equilateral_triangle

https://en.wikipedia.org/wiki/Arc_length