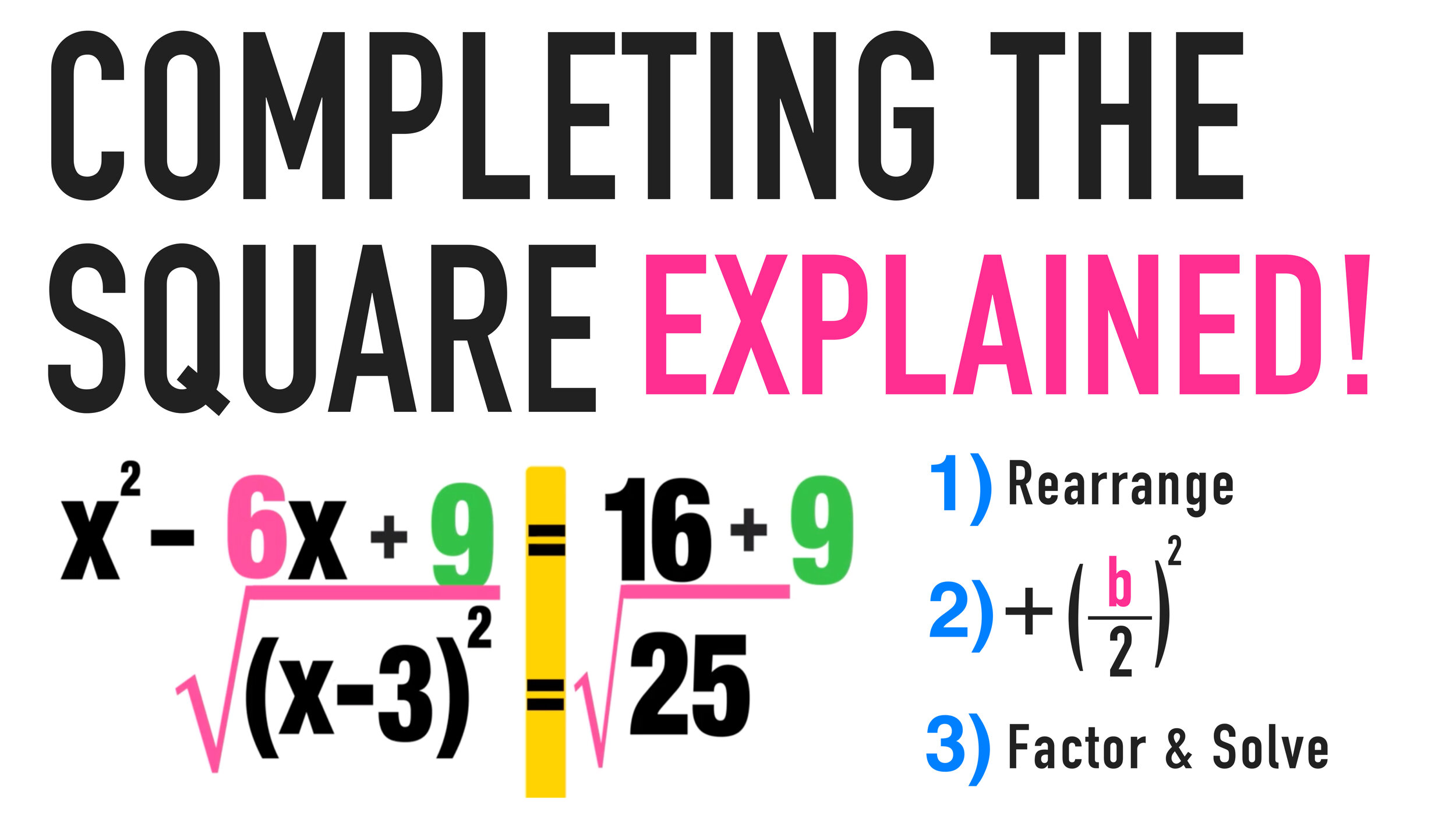How to Find the Vertex of a Parabola?

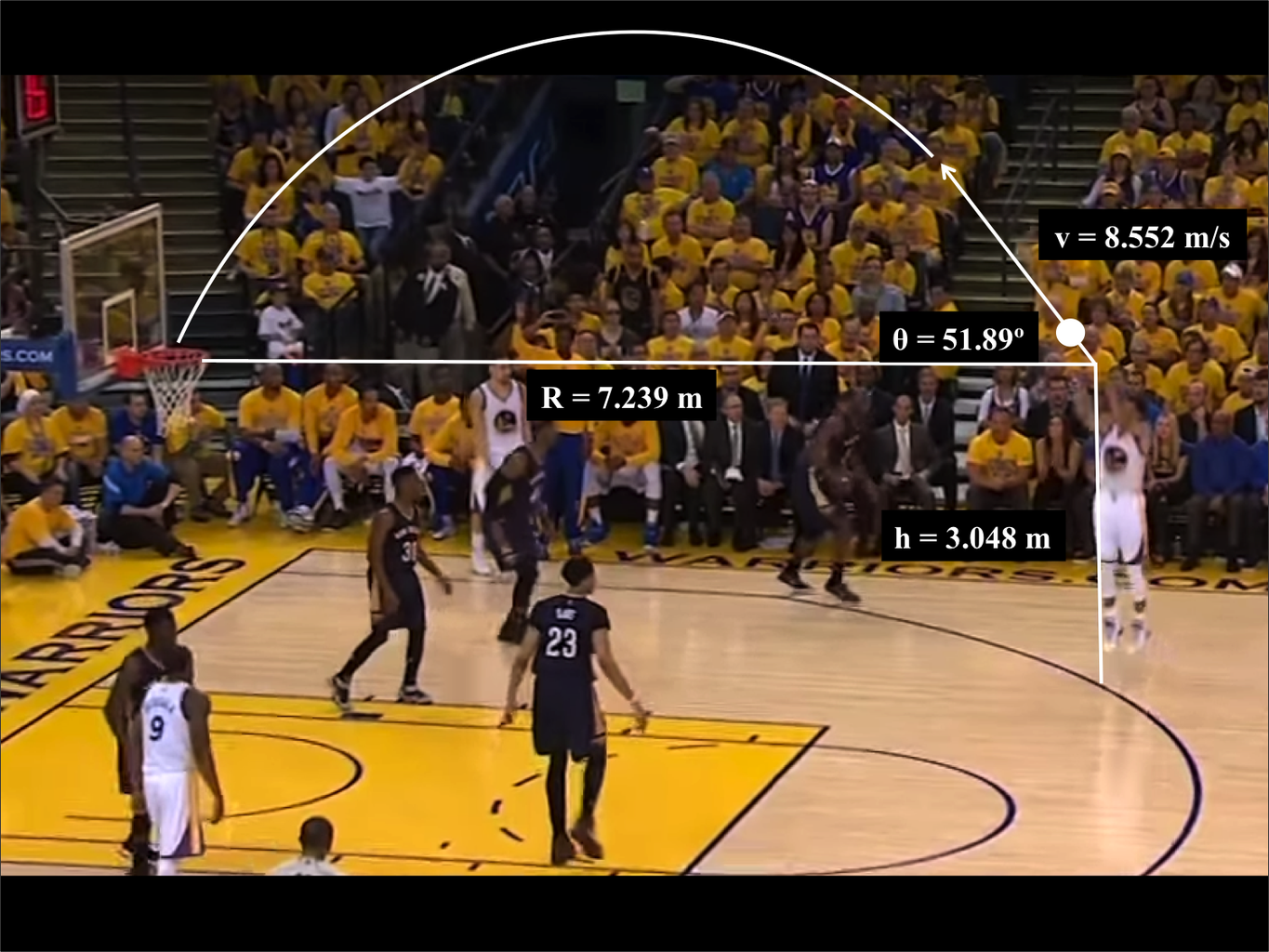
Have you noticed when throwing a basketball into the air that its trajectory forms a perfect arc? In geometry terms, this shape is known as a parabola; at its highest point along its path lies its vertex, which determines whether it passes accurately through its target hoop. Understanding its role not only unlocks basketball trajectories but can be applied widely throughout bridge design, satellite antenna optimization, and many other fields; in this article, we'll also cover various methods for finding its vertex to easily unlock this fascinating intersection between mathematics and real-world applications!

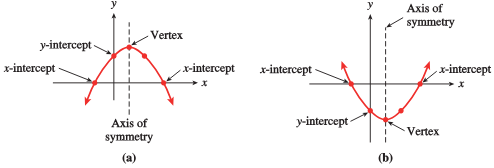
Definition and Basic Properties of the Vertex  

Mathematical Definition of a Parabola and Its Vertex  

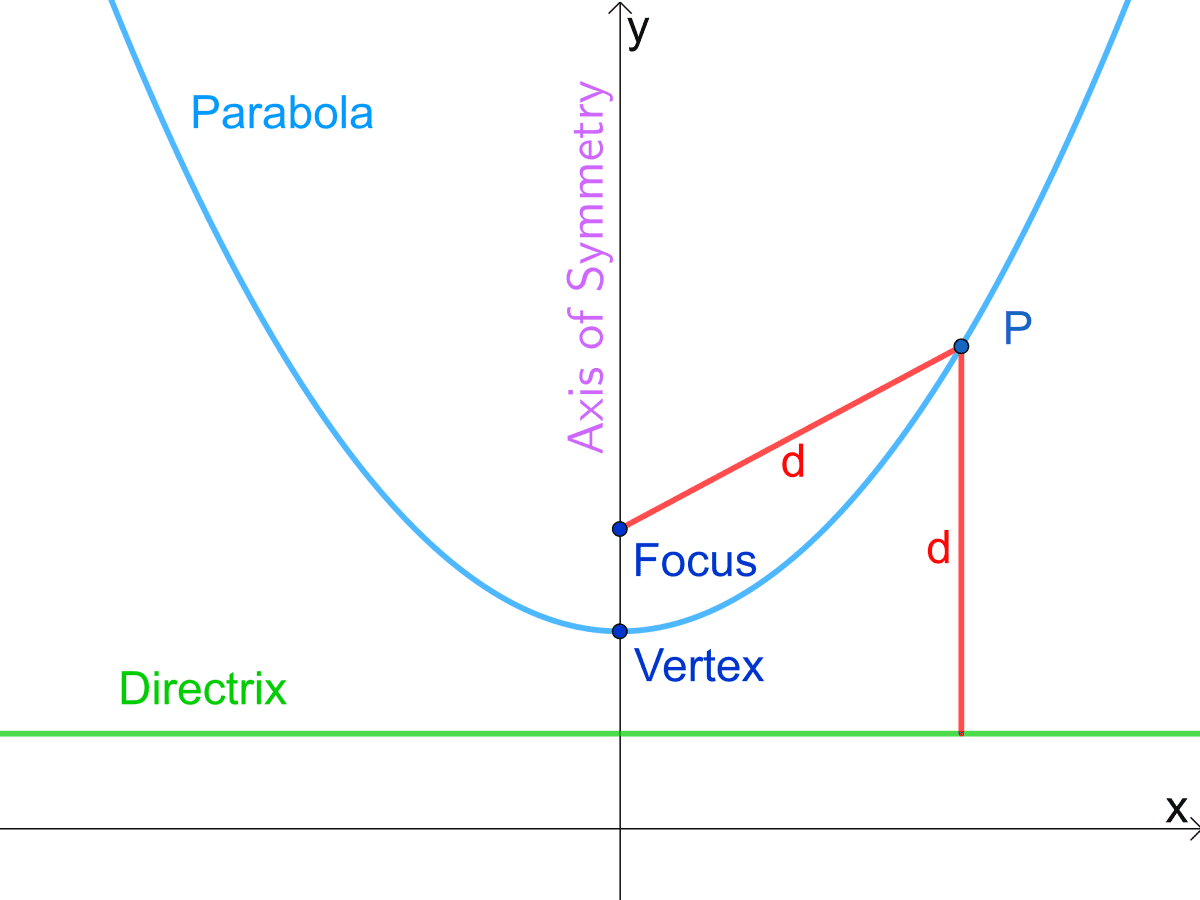
Parabolas are loci that lie equidistant from both fixed points (the focus) and lines (the directrix). Geometrically, parabolas form as perfect mirror images on either side of their axis of symmetry - their vertex being precisely this "balance point," where neither bias toward focus nor away from directrix occurs. Solar cooker reflective surfaces often take the shape of rotating parabolas with heat most concentrated near their vertex region.

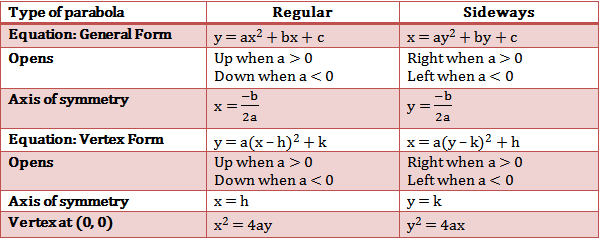
Algebraically, the general equation of a parabola can be expressed using its general equation, as shown below.

\(y = ax^2 + bx + c\) (opening upward or downward)  

or  

\(x = ay^2 + by + c\) (opening sideways).  

Vertex coordinates \((h,k)\) are unique points within an analytical expression that are independent of quadratic terms, thus indicating where the inflection of a function lies.

The Role of the Vertex in a Parabola  

Determining the Extreme Value (Minimum/Maximum)  

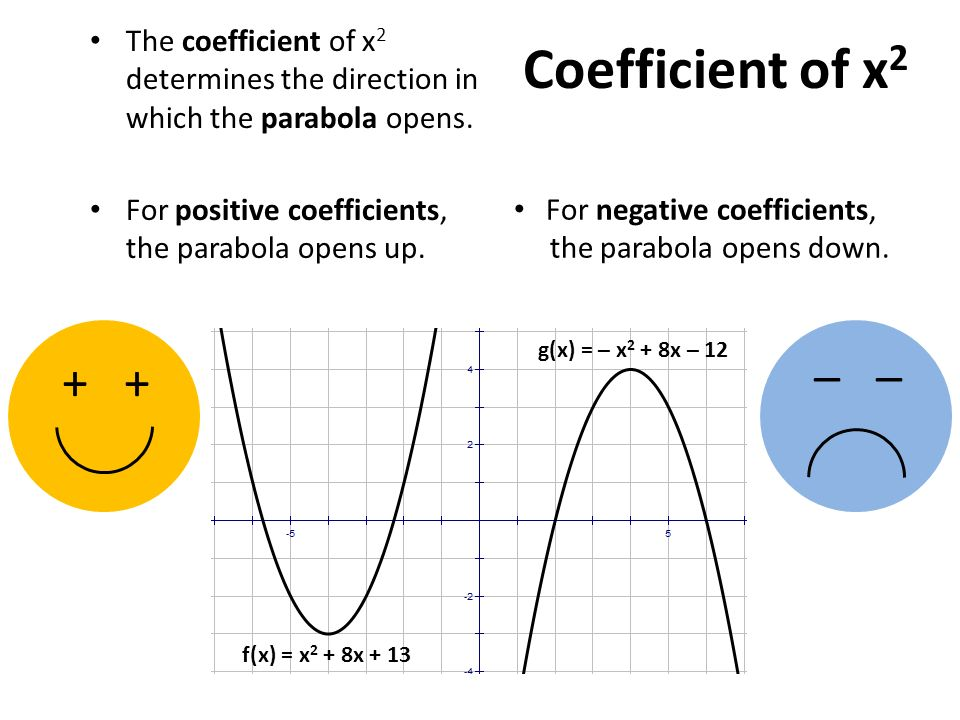
Parabolas that open upward (i.e., \(a > 0\))typically feature the vertex as their minimum point; when opening downward (i.e., \(a < 0\)), however, their vertex becomes their maximum point; such as in an arch bridge support point or projectile trajectory peak moment. An ejection seat safety height is determined directly by this vertex position within its trajectory's \(k\)coordinate - providing that its maximum remains below 3 kilometers; these parameters \(a\) and \(b\). These parameters can also be strictly managed.

Geometric Connection with the Axis of Symmetry  

Vertex location can be identified using its horizontal coordinate.

\(h = -\frac{b}{2a}\),

determines both the position and horizontal shift of parabolas. Architectural examples like the Sydney Opera House's roof consist of segmented parabolas whose symmetry axes must align with key support points to distribute stress evenly and ensure stress distribution is also distributed equally across each segmented parabola roof section.

Classification of Parabola Forms and Vertex Formulas  

Calculating Vertex Coordinates in the Standard Form  

Formula for Upward/Downward Opening Parabolas  

For standard form,

\(y = 2x^2 + 4x - 3\),  

we begin by calculating the horizontal coordinate of a vertex using this formula

\(h = -\frac{b}{2a}\).  

\(a = 2\) and \(b = 4\). Once we have this number, we know the vertex position.

\(h = -\frac{4}{2 \times 2} = -1\).  

substitute \(x = -1\) into the equation to find vertical coordinates;

\(k = 2(-1)^2 + 4(-1) - 3 = -5\).  

thus locating the vertex as \((-1, -5)\). This technique works for any quadratic function - just remember to pay special attention when performing sign calculations so as not to cause errors in calculation.

Formula for Sideways Opening Parabolas  

For a sideways parabola given by  

\(x = \frac{1}{2}y^2 - 3y + 4\),  

by analogy with the standard vertex formula, we obtain  

\(k = -\frac{-3}{2 \times 0.5} = 3\),  

and then  

\(h = \frac{1}{2}(3)^2 - 3(3) + 4 = 4.5 - 9 + 4 = -0.5\).  

Vertices for such parabolas can be recorded as \((-0.5, 3)\). Parabolas such as these are frequently seen when modeling particle trajectories in centrifugal devices.

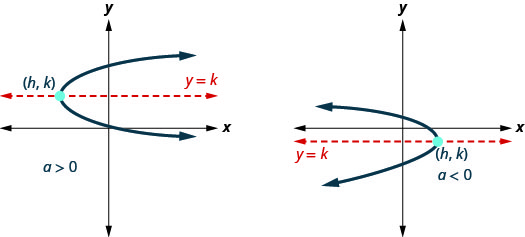
Vertex Form and Reading the Vertex Directly  

Upward/Downward Opening Form  

If the equation is given as  

\(y = -2(x+3)^2 + 4\),  

Vertex \((-3,4)\) can be easily identified using an equation written in vertex form whereby term \((x+3)^2\) indicates a horizontal shift to \(-3\) while constant \(4\) represents an upward vertical shift of 4 units. A negative coefficient such as\(-2\)indicates that the parabola opens downward so that the vertex (maximum point of the graph) marks its maximum point during the flight. Such an equation often comes into play when modeling rocket flight under frictional deceleration, where the vertex marks the highest point during its path during flight.

Sideways Opening Form  

If the equation is given as  

\(x = 0.5(y-1)^2 - 2\),  

Vertex coordinates are quickly identified when they are set equal to \((-2, 1)\) in this equation. A positive coefficient of 0.5 denotes that the parabola opens to the right instead of opening vertically like most curves; its axis of symmetry runs horizontally for easy analysis of right-opening parabolas used for practical engineering applications like optimizing signal reception areas of satellite parabolic antennas to ensure efficient communication and accurate targeting; such designs are indeed fundamental elements in successful satellite system deployment and utilization.

Special Technique for Converting from Intercept Form  

Given a parabola in intercept form  

\(y = 3(x-1)(x-5)\),  

its roots are \(x = 1\) and \(x = 5\):  

1. The horizontal coordinate of the axis of symmetry is  

\(h = \frac{1+5}{2} = 3\);  

2. Substitute back into the original equation to obtain  

\(k = 3(3-1)(3-5) = 3 \times 2 \times (-2) = -12\);  

So, it is easy to quickly determine the vertex \((3, -12)\), making it suitable for quickly placing support points on engineering blueprints.

Integration of Multiple Methods for Vertex Determination  

Three-Step Completing the Square Method (Standard Form → Vertex Form)

Step 1 – Coefficient Extraction:  

Start with the equation  

\(y = 2x^2 - 12x + 7\).  

Make an attempt to factor out the coefficient from quadratic and linear terms until obtaining:

\(y = 2(x^2 - 6x) + 7\).  

This isolates quadratic expression for easier manipulation.

Step 2 – Completing the Square:  

Calculate \(\left(\frac{-6}{2}\right)^2 = 9\).  

Add and subtract this value from within the parentheses to transform an expression into an equation.

\(y = 2(x^2 - 6x + 9) + 7 - 2 \times 9\).  

This step produces an ideal square trinomial.

Step 3 – Simplification:  

Rewrite the trinomial as a perfect square:

\(y = 2(x-3)^2 - 11\).  

Here, the vertex can be easily identified as \((3, -11)\). Furthermore, coefficient balancing must remain carefully balanced throughout.

Using the Midpoint of the Roots in the Intercept Form to Find the Vertex  

For the equation \(y = -(x+4)(x-2)\), follow these steps:  

• The roots are at \(x = -4\) and \(x = 2\), with Midpoint of the Roots

\(x = \frac{-4 + 2}{2} = -1\);  

• Substitute \(-1\) into the original equation to compute  

\(y = -(-1+4)(-1-2) = -3 \times (-3) = 9\);  

Thus, the vertex \((-1,9)\) marks the highest point on this parabola; economics uses this strategy for finding peak revenue levels.

Comparative Analysis of the Direct Formula Method  

Comparison case:  

• For the equation \(y = 0.5x^2 + 3x - 4\):  

Applying directly the formula \(h = -\frac{3}{2 \times 0.5} = -3\), rather than performing the square method is more efficient and time-saving;

• For the equation \(x = 2y^2 + 5y + 1\):  

Sideways parabolas require a different way of thinking in order to prevent mixing up vertical and horizontal coordinate formulas.

Common Pitfalls and Precautions  

The Impact of Coefficient Signs on the Vertex’s Displacement

Understanding how the signs of coefficients can significantly change the orientation and displacement of parabola vertex is paramount to successful interpretation, for instance when working with equations as complex as this one. Take an example form our question bank:

\(y = -x^2 + 4x\).  

In this case, if one happens to miss the negative sign preceding the quadratic term inadvertently, one might incorrectly conclude that vertex \((2,4)\) represents a minimum point rather than its true maximum and draw inaccurate conclusions about its behavior. Similarly, take the equation  

\(x = 3y^2 - 6y + 1\).  

Erroneously interpreting the sign of coefficient \(a = 3\)could result in thinking the parabola opens to the left when, in fact, it opens to the right. These examples demonstrate the need to carefully consider coefficient signs in any quadratic model to ensure accurate analysis and interpretation of vertex displacement.

Special Consideration of Extreme Values in Sideways Opening Parabolas  

Sideways parabolas do not exhibit extreme vertical values yet still play an essential part. Their vertex positions still play an integral part in an encrypted signal receiver's coverage area determination process; for example, in one such configuration

\(x = 0.2y^2\),  

Where the horizontal coordinate of a vertex corresponds with compensation required to account for installation error.

Application Scenarios and Mathematical Models  

Calculating the Projectile’s Vertex in Physics  

An initial velocity of \(v_0 = 200 \, \text{m/s}\)and launch \(\theta = 30^\circ\)are necessary conditions for an ideal cannonball trajectory; its trajectory can then be described using this equation:

\(y = -\frac{g}{2v_0^2\cos^2\theta}x^2 + \tan\theta \, x\).  

Substituting these values into the vertex formula yielded an accurate maximum height \(k = 510 \, \text{m}\), along with an appropriate horizontal distance \(h = 1765 \, \text{m}\) that helped pinpoint where evacuation should begin at landing zones.

Optimization Problems of Parabolas in Engineering Design  

For the main span of Sydney Harbour Bridge's main span design equation is

\(y = 0.002x^2 - 1.2x + 150\).  

Based on this quadratic model, its vertex location is determined. \(h = 300 \, \text{m}\) and \(k = 30 \, \text{m}\).  

Vertex coordinates play an essential role in establishing the ideal height of main towers, ensuring stress distribution is optimal throughout their structure. Their use led to an 18% decrease in steel requirements - evidence of how mathematics can aid resourceful engineering design.

Vertex Analysis of Revenue/Cost Functions in Economics  

Consider a company's profit model given by  

\(P(x) = -0.4x^2 + 120x - 800\).  

By applying the vertex formula, we found the optimal production level was 150 units, which represents an estimated profit of 8900 Yuan. Any deviation from this optimal production level, such as producing only 140 units instead, would result in an approximate reduction in profit of 6%, highlighting the vital role accurate production planning plays in optimizing returns and driving overall business performance.

Theoretical Derivation of the Vertex Formula  

Detailed Algebraic Process of the Completing the Square Method  

Starting from the general form  

\(y = ax^2 + bx + c\):  

1. Coefficient separation: Separate quadratic and linear terms by writing them separately in written form.

\(y = a\left(x^2 + \frac{b}{a}x\right) + c\);  

2. Constructing the perfect square: add the term  

\(\left(\frac{b}{2a}\right)^2\) to complete the square, that is,  

\(y = a\left(x^2 + \frac{b}{a}x + \frac{b^2}{4a^2}\right) - a \cdot \frac{b^2}{4a^2} + c\),  

at which point the expression inside the parenthesis becomes \(\left(x+\frac{b}{2a}\right)^2\);  

3. Extracting the vertex: rearrange to obtain  

\(y = a\left(x+\frac{b}{2a}\right)^2 + \left(c - \frac{b^2}{4a}\right)\),  

so that the vertex is  

\((h,k)=\left(-\frac{b}{2a}, c - \frac{b^2}{4a}\right)\).

Proof of the Relationship between the Discriminant \(D\) and the Vertex Coordinates 

By equating with the discriminant  

\(\Delta = b^2 - 4ac\),  

Vertical Coordinate of Vertex as follows.

\(k = c - \frac{b^2}{4a} = -\frac{\Delta}{4a}\).  

Once again, this can be seen:

When \(\Delta > 0\), the vertex lies along its perpendicular bisector of the line segment joining both roots;

If \(\Delta = 0\), its vertex coincides with its unique intersection point between the parabola and x-axis;

When \(\Delta < 0\), its value determines which direction the vertex's vertical coordinate will take; for instance, if \(a>0\), parabolas shift upward.

Vertices of parabolas have always served as the pivot of mathematics - from perfect basketball arcs soaring through the sky to exquisite balance between forces and beauty in suspension bridge designs - as a source of leverage between mathematics and real life. Finding a vertex involves applying techniques like the completing-square method or midpoint-of-roots technique with precision in order to deconstruct an equation or strategically applying both of them as part of key coordinate capture techniques - it all serves to convert abstract mathematical language into laws that govern real-life situations. Keep this in mind the next time you enjoy gazing upon a fountain's spectacular splash or marveling at precision calculations for missile interception: Every vertex coordinate is evidence of profound connections among mathematical definitions, geometric intuition, and physical laws.

reference:

https://en.wikipedia.org/wiki/Vertex_(geometry)

https://en.wikipedia.org/wiki/Parabola

https://en.wikipedia.org/wiki/Extreme_value_theorem