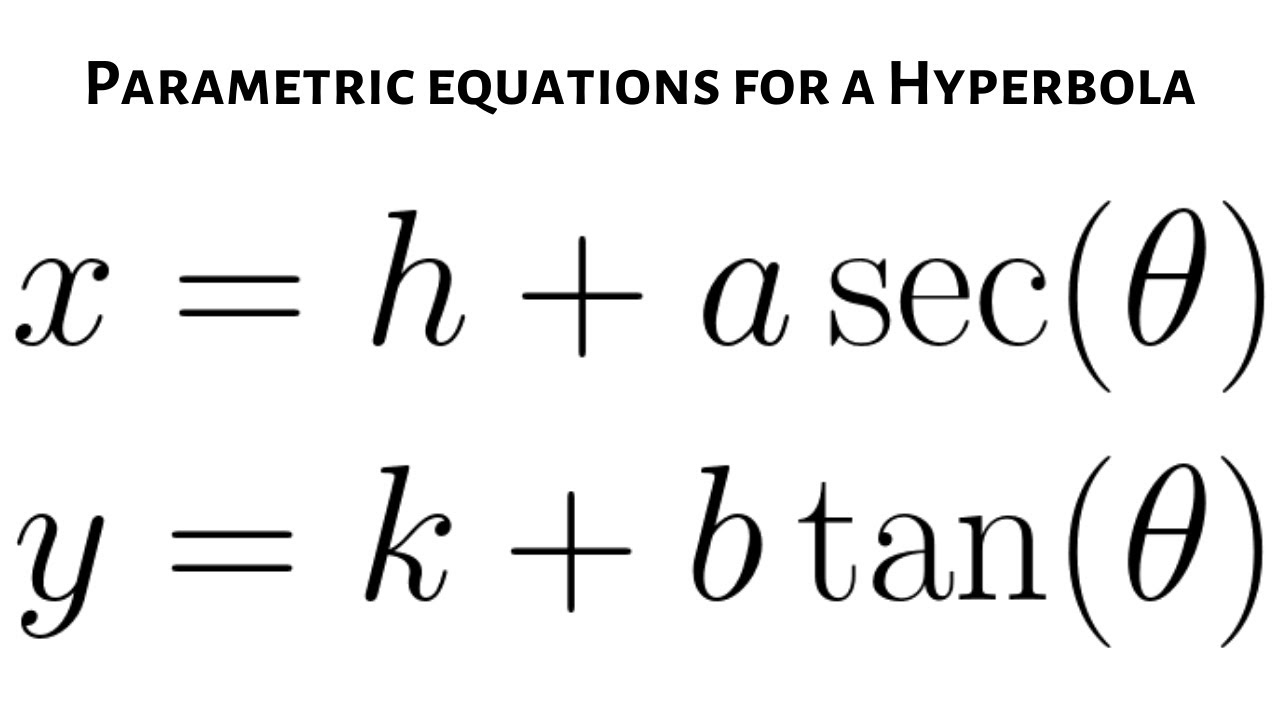What Is a Hyperbola?

Everyday life contains hyperbolas that might seem unfamiliar or distant—for example, celestial motion when spacecraft are passing near Earth; the architectural designs of many bridges also use principles from hyperbola design as their cornerstone. This special curve not only holds deep mathematical meaning but pervades much of what we take for granted each day.

Hyperbolas are unique conic sections with fascinating geometric and practical applications, captivating scholars for decades. But exactly what are hyperbolas, and what are their definition, properties, equations, and uses? We will now go further by breaking them down step-by-step to uncover all their mysteries!

Overview of Hyperbolas

What Is a Hyperbola?  

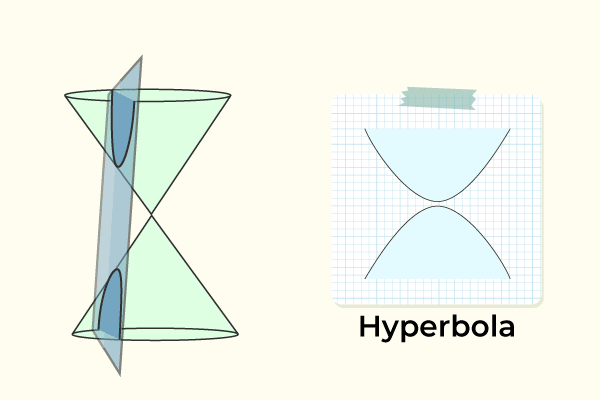
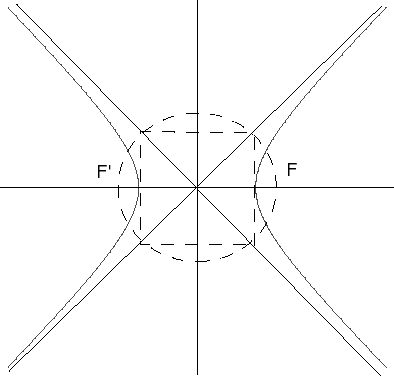
Hyperbolas are conic sections composed of plane and double-cone intersections. Geometrically, a hyperbola forms when one plane intersects both nappes of a conical surface at an acute angle to its axis without passing through its vertex; analytic geometry views this characteristic as core to any hyperbola: any point on it with two fixed points called foci remains within an absolute difference of distance constant between points on it and these foci.

Hyperbolas are singular geometric figures, each consisting of two symmetrical branches that extend indefinitely while asymptotically approaching certain lines (the asymptotes) without ever crossing them. Their intricate design provides the basis for subsequent mathematical analyses and practical applications.

Applications of Hyperbolas  

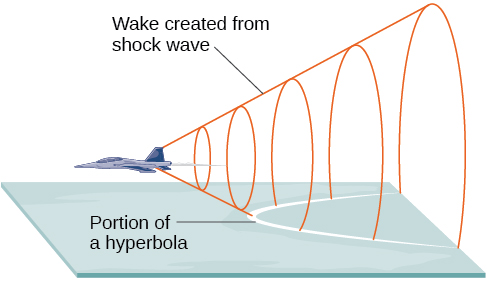
Hyperbolas' geometric properties make them highly valuable in various applications, from scientific calculations of spacecraft orbits to communications technologies and telescope designs. When an approaching spacecraft approaches planet at extremely fast speed, its path may often resemble that of a hyperbola; this phenomenon is commonly referred to as gravitational slingshot effect. Hyperbolas also play an essential part in depicting electromagnetic wave propagation as well as reflecting properties of light; making them indispensable components in communication technologies and telescope designs.

Engineering also utilizes hyperbolas in bridge designs. For instance, arch bridge designs often employ hyperbolic structures in order to maximize load-bearing performance and ensure overall stability.

Definition and Components of a Hyperbola

Core Definition  

Hyperbolae are mathematical constructs defined geometrically as follows.

Constant Difference in Distances to Foci  

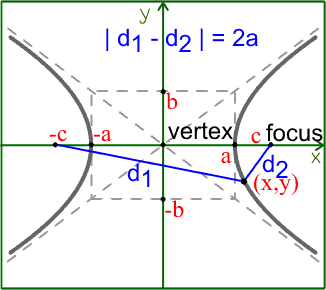
Hyperbolas can be defined as sets of points on a plane whose absolute difference from two fixed points (called foci ) remains constant over time, mathematically expressed as:

\(|d_1 - d_2| = 2a\)

Where \(d_1\) and \(d_2\) represent distances from points on a hyperbola to its foci and 2a is constant - thus distinguishing hyperbolas from other conic sections.

Symmetry and Trajectory Characteristics  

Hyperbolas display unique geometric symmetry. Their center point is symmetrical while they contain two perpendicular axes (transverse and conjugate axis). Furthermore, each hyperbola branch extends in opposite directions indefinitely in both dimensions forming characteristically symmetrical trajectory lines.

Geometric Components 

To gain a comprehensive knowledge of hyperbolas, we must examine their primary geometric elements:

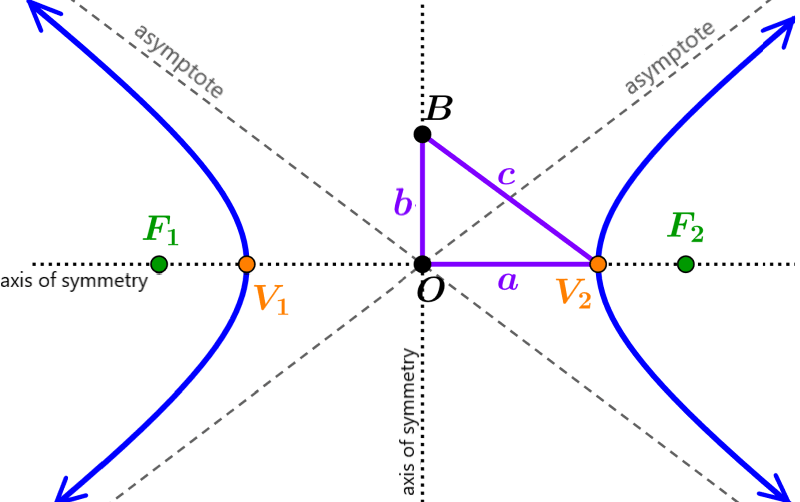
Vertices, Foci, and Center  

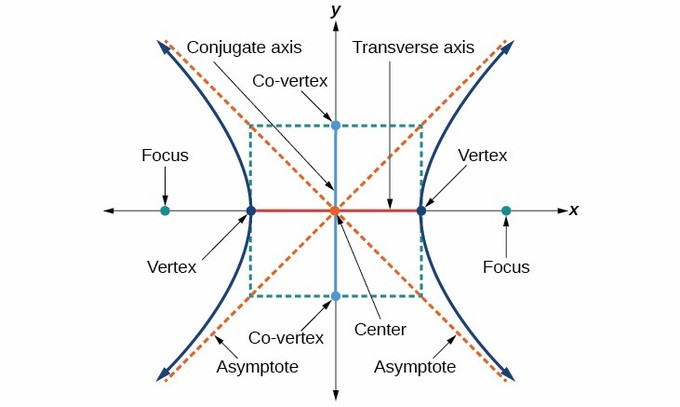
A hyperbola contains two vertices that connect its transverse axis with its edges, two foci that form fixed points along its curve, and its center, located halfway between these foci.

Transverse Axis and Conjugate Axis  

The transverse axis is defined as an axis perpendicular to both conjugate axes that passes through the center and defines the primary direction in which the hyperbola opens. Conversely, conjugate axes determine branch width.

Asymptotes, Directrices, and Latus Rectum  

Asymptotes of hyperbolae are straight lines that the branches approach infinitely but never touch, while directrices serve as auxiliary lines related to foci and define their geometry. A latus rectum represents another significant geometric feature by being perpendicular to the transverse axis while passing through focus(es).

Equations and Derivation of a Hyperbola  

Standard Equations and Classification  

Hyperbola equations are widely known in analytic geometry and frequently expressed using standard forms. Hyperbolas may be divided into two main groups depending on where their foci lie:

  Hyperbolas with Foci on the x-axis or y-axis  

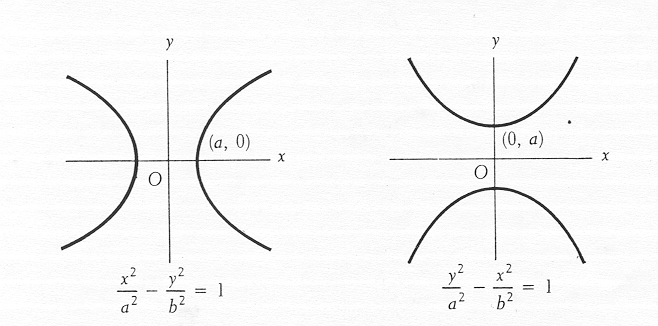
1. Hyperbolas with foci on the x-axis:  

When the foci of a hyperbola are located on the x-axis, its standard equation is:  

\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\)

Here, \(2a\)) is the length of the transverse axis; \(2b\) is its conjugate counterpart; foci are located \(（\pm c, 0)\),; therefore the relationship \(c^2 = a^2 + b^2\) holds true.

2. Hyperbolas with foci on the y-axis: 

When both foci are located along the y-axis, the standard equation for hyperbolas becomes:

\(\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\)

As with the primary axes, \(2a\) represents the length and \(2b\) its width respectively; foci of this curve lie on zero at point \((0, \pm c)\) under condition that \(c^2 = a^2 + b^2\).  

Rectangular Hyperbolas  

A rectangular hyperbola is a special case of hyperbola where both transverse axis lengths equal conjugate axis lengths (\(a = b\)). Thus, its standard equation simplifies to:

\(\frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 \quad \text{or simply} \quad x^2 - y^2 = a^2\)

Rectangular hyperbolas have distinctive geometric properties, including asymptotes that always intersect in perpendicular fashion and an easier solution when performing algebraic and geometric analyses.

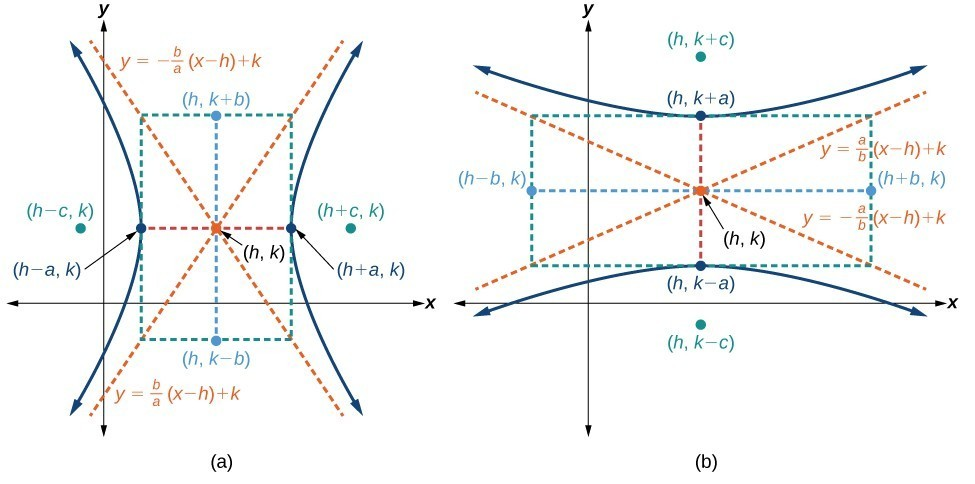
Translated and Rotated Equations of a Hyperbola  

At times, we need to shift or rotate a hyperbola away from its origin; to accommodate such shifts and rotations, we utilize translated and rotated forms of its equation:

1. Translated Hyperbolas:  

If we shift the center of a hyperbola from \((0, 0)\) to some new position \((h, k)\) then its standard equation becomes:

\(\frac{(x - h)^2}{a^2} - \frac{(y - k)^2}{b^2} = 1\)

This form can be applied to hyperbolas whose centers lie at any coordinate.

2. Rotated Hyperbolas:  

Rotated hyperbolas can be particularly helpful in areas of geometric and physical applications where rotation by an angle \(\theta\) requires its equation to reflect this transformation by substituting rotated coordinates into its original equation, maintaining all essential characteristics while becoming more complex than their unrotated counterpart. Rotated hyperbolas offer considerable versatility.

Properties of a Hyperbola  

Definition and Equation of Asymptotes  

Asymptotes of a hyperbola are lines that the branches approach infinitely but never intersect, acting as geometric reference lines that define both its symmetry and shape.

For the hyperbola given by the equation \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\), its asymptotes are:  

\(y = \pm \frac{b}{a} x\)

Similarly, for the hyperbola \(\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\), the asymptotes are:  

\(y = \pm \frac{a}{b} x\)

Asymptotes are straight lines that define where branches of a hyperbola extend in two dimensions and also serve to describe its overall shape and orientation, offering visual aid when graphing or analyzing this form.

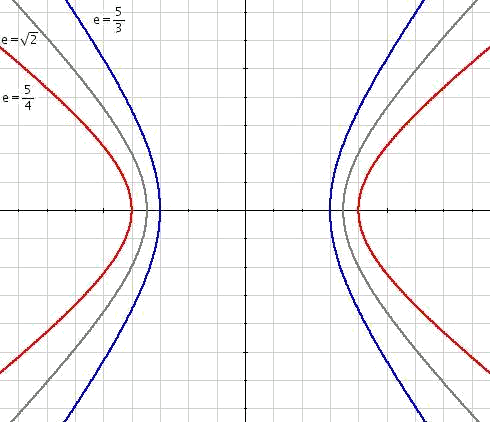
Meaning and Formula for Eccentricity  

The eccentricity (\(e\)) is an essential parameter that measures the shape of hyperbolas. It can be defined as the ratio between the distance between foci (\(c\)) and the length of the semimajor axis (\(a\)):  

\(e = \frac{c}{a} \quad \text{where} \quad e > 1\)

An eccentricity greater than 1 indicates that both branches of a hyperbola feature wider openings and appear flatter; on the contrary, smaller eccentricities indicate sharper and more compacted branches. A condition defined as \(e > 1\)differentiates hyperbolas from similar conic sections such as ellipses (\(e < 1\)) or parabolas(\(e = 1\)).

Symmetry and Image Characteristics  

Hyperbolas display several forms of symmetry:

1. Center Symmetry: Hyperbolas display center symmetry. Every point on their hyperbola has an opposite point through their center that mirrors them exactly.

2. Axial Symmetry: Hyperbolas are easily classified and analyzed thanks to their strong axial symmetry. They share transverse and conjugate axes, which makes calculating these hyperbolic curves effortless.

An image of a hyperbola depicts two branches that mirror one another and connect at an inflection point, each beginning from one vertex and extending toward its respective asymptote - creating the iconic open curves characteristic of hyperbolas.

Special Hyperbolas: Rectangular Hyperbolas  

Rectangular hyperbolas are an exclusive subclass of hyperbolas in which both transverse and conjugate axes measure equal length (\(a = b\)). Their standard equation can be written as:

\(\frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 \quad \text{or simplified as} \quad x^2 - y^2 = a^2\)

The asymptotes of a rectangular hyperbola are always perpendicular, given by:  

\(y = \pm x\)

This hyperbola type is easy to work with both algebraically and graphically, making it popular in practical applications, including signal transmission and optical reflections, due to its geometric simplicity and symmetry.

Parametric Representation and Graphs of a Hyperbola  

Parametric Equations of a Hyperbola  

Parametric equations offer an efficient means of representing points on curves when studying hyperbolas, eliminating the need to solve algebraic equations while providing an intuitive representation. When applied to standard hyperbolic equations such as: \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\), parametric equations appear as:

\(x = a \sec\theta \quad \text{and} \quad y = b \tan\theta\)

Here, \(\theta\) serves as a parameter, representing the angle formed between any point on a hyperbola and transverse axes via the focal axis. These parametric equations enable any point \((x, y)\) on any hyperbola to be directly expressed using its value of \(\theta\).  

Also, for hyperbolas with their foci located along the y-axis and described by equation \(\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\), their parametric representation becomes:

\(y = a \sec\theta \quad \text{and} \quad x = b \tan\theta\)

Parametric representation not only simplifies computations but is widely employed for graph plotting and numerical algorithms dealing with hyperbolas - making geometric analysis more efficient overall.

If you still have questions about parametric equations, feel free to consult our AI tutor. It offers expert analysis to help you solve problems, enhance your learning efficiency, and guide you toward success.

Graphing and Analysis of a Hyperbola  

Shape of the Graph in Standard Form  

Hyperbola graphs consist of two branches that are symmetrically related around both transverse and conjugate axes. With respect to an equation such as\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\), for which the transverse axis is the horizontal axis, and the two branches open along it. The vertices of the hyperbola are located at \((a, 0)\) and \((-a, 0)\).  

Key features of the graph:  

Opening Direction: Depending on whether its focal axis is horizontal or vertical, branches of a hyperbola open along either its transverse or conjugate axes.

Asymptotic Behavior: Each branch approaches but never intersects its respective asymptotes, creating a smoothly expanding appearance.

Symmetrical Structure: Every branch features its mirrored counterpart for perfect symmetry across axes or the center.

Role of Eccentricity in Graph Shape  

Eccentricity(\(e\)) directly affects the shape of a hyperbola's graph. When its eccentricity\(e\) is close to 1, its branches tend to be steeper and closer together, congregating around its vertex. As its eccentricity increases, its branches open wider, becoming flatter as more of its branches spread apart and create a flatter pattern of curves.

Eccentricity may have various impacts, including:

1. At an \(e \to 1\), the hyperbola branches resemble parabola's curves.

2. At \(e \gg 1\), its branches move nearly parallel with asymptotes for a flatter curve.

Eccentricity plays an integral part in defining the geometry of hyperbolas. Variations in their shapes have significant ramifications for practical fields like optics and satellite communication systems, where their level of curvature directly affects performance.

Applications of a Hyperbola  

Applications in Engineering  

Hyperbolas have long been utilized as an engineering design element. Their geometric properties have proven invaluable when applied to bridge and structural designs; for example, some arch bridge designs take inspiration from hyperbola's curvilinear form; this not only looks good visually, but it effectively distributes pressure while improving stability and load-bearing capacities of structures.

Hyperbolas have also proven their worth in numerous large energy projects, showing their practical use as design elements of cooling towers for nuclear power plants. Their form allows efficient airflow, optimal heat dissipation, and structural stability—qualities that benefit nuclear plant cooling tower designs in particular. Hyperbolic designs have proven invaluable tools in industrial engineering.

Applications in Science  

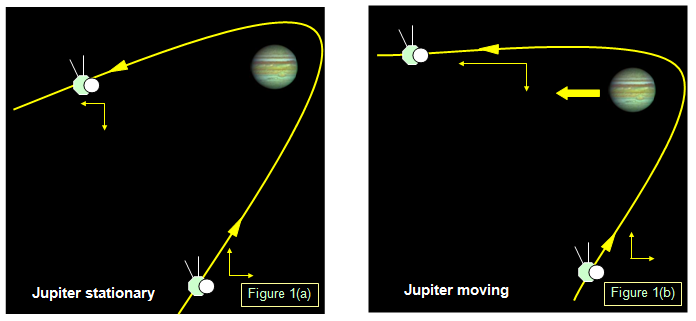
Hyperbolas have many applications within science, particularly physics and astronomy. When spacecraft encounter the gravitational pull of celestial bodies, their trajectory often follows a hyperbolic curve known as the gravitational slingshot effect; by exploiting this phenomena efficiently they can rapidly change speed and direction with minimal fuel use, opening up long distance interstellar exploration possibilities.

Hyperbolas have long been used as focal properties to design high-precision mirrors and antenna systems such as radar dishes or satellite receivers; their effective ability to reflect or focus light efficiently leads to enhanced communication technologies as well as observational devices.

Hyperbolas also play an integral role in electronics, particularly when creating filter circuits. Their mathematical properties help design effective frequency separation methods to meet signal processing specifications and needs.

Further Exploration  

Comparison Between Hyperbolas and Other Conic Sections  

Similarities and Differences with Parabolas and Ellipses  

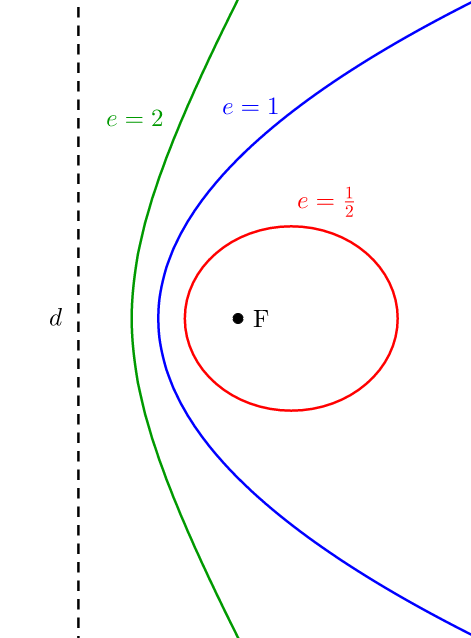
Conic sections encompass ellipses, parabolas, and hyperbolas; their differentiation can usually be determined through eccentricity and geometric structures:

1. Differences in Eccentricity:  

Ellipses have an eccentricity (\(e\)) satisfying an eccentricity condition of less than 1, meaning the distance between foci is shorter than its major axis length.

parabolas: Eccentricity is exactly \(e = 1\), meaning distance to focus equals distance from directrix.

Hyperbolas: Eccentricity must satisfy \(e > 1\)as defined above, and the distance between foci exceeds that of transverse axis length.

2. Differences in Geometric Structures:  

Ellipses form closed curves that are symmetrical around both axes, and parabolas have one open curve that extends infinitely in a direction.

Hyperbolas consists of two open branches connected by two symmetrical branches that extend infinitely in opposite directions while asymptotically approaching certain reference lines (asymptotes).

By comparing these properties, one can understand that hyperbolas stand apart among conic sections by virtue of their two branches and eccentricity exceeding 1.

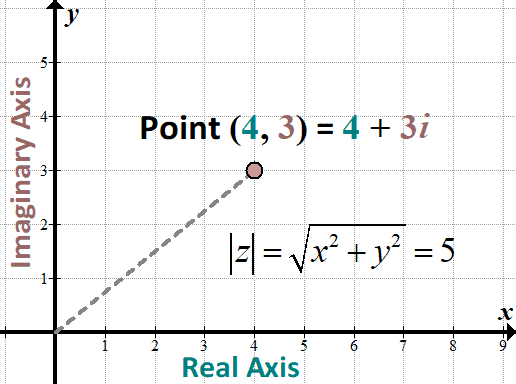
Hyperbolas in the Complex Plane  

Hyperbola Equations in the Complex Plane  

Hyperbolas can be represented on the complex plane using complex numbers, making rotation and transformation analysis much simpler. A hyperbolic equation such as \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\) may be expressed using complex number format as follows.

\(z \cdot \overline{z} = 1 + \left(\frac{y}{b}\right)^2\)

where \(z = x + iy\). This representation broadens our study of hyperbolas, providing new ways of looking at them across multidimensional spaces.

Parametric Representation and Geometric Significance in the Complex Plane  

On the complex plane, hyperbolas may also be parameterized using complex variables for easier geometric transformations such as translations, rotations and reflections. By mathematically outlining position and angle calculations for hyperbolic curves in use in signal processing and image modeling fields.

Hyperbolas' advanced perspective offers major implications in disciplines where mathematical models must describe complex spaces, enabling deeper exploration of both theory and practice regarding hyperbola geometry.

Hyperbolas play an indispensable role both mathematically and practically, from geometric definition to parametric equations and property analysis, from practical implementations to their applications. Their versatility is evident everywhere they're found—space exploration, engineering design, and scientific instruments use them frequently while remaining invisible yet essential tools; by studying hyperbolas comprehensively, we observe their ability to combine beauty with utility, unlocking unimaginable potential.

reference:

https://en.wikipedia.org/wiki/Hyperbola

https://en.wikipedia.org/wiki/Ellipsis

https://en.wikipedia.org/wiki/Circle