How to Find the Volume of a Cylinder

Everyday objects have an intricate connection with geometric forms. Common items like beverage cans and oil drums often take the shape of a cylindrical container, and while shopping at the supermarket, you might have been attracted by an array of can foods with their beautiful appearance and regular design that made transport easy. Real-life examples highlight the significance of understanding volumetric analysis for everyday living and scientific endeavors. This article begins with basic concepts before gradually exploring properties, formulae, and applications of cylindrical objects - with the ultimate aim of helping everyone better comprehend and master this knowledge as it provides a solid theoretical base.

Basic Concepts  

Definition and Significance of Three-Dimensional Volume  

Three-dimensional volume is an invaluable measure of space occupied by solid objects, not only revealing their physical dimensions but also playing an essential role in many fields like engineering design, modeling, and packaging. Understanding volume allows us to appreciate space utilization efficiently while providing us with a basis for selecting materials and creating structures. In-depth exploration of its nature also allows us to better grasp an object's distribution across space as well as potential uses - providing theoretical support when solving practical issues.

Definition and Construction of a Cylinder  

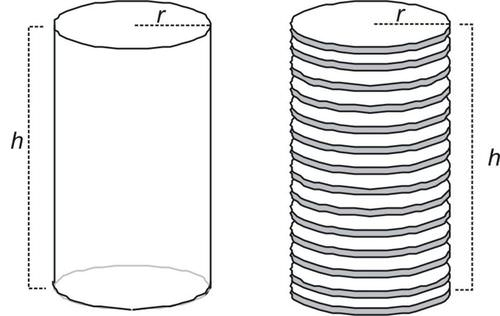
A cylinder is a three-dimensional geometric figure composed of two identical circular bases connected by an intermediate surface. A right circular cylinder can be identified when its base is perpendicular to its lateral surface; its lateral surface can then be seen as an unwrapped rectangle from its circumference, thus creating a regular geometric form. Cylinders can be divided into two main types based on their internal structures: hollow and solid. Each type corresponds with a distinct method for volume calculation and application scenarios, so mastery of basic three-dimensional volume and construction principles provides the basis for understanding subsequent formulae and calculations, providing a firm theoretical grounding for various practical applications.

Formulas for Volume and Calculation Methods

Basic Formula for Right Circular Cylinder  

Volume of a right circular cylinder can be calculated directly by multiplying its area by its height, with the radius being represented as R and height as H; henceforth

\(V = \pi r^2 h\)  

This straightforward formula serves as the cornerstone for solving various practical problems.

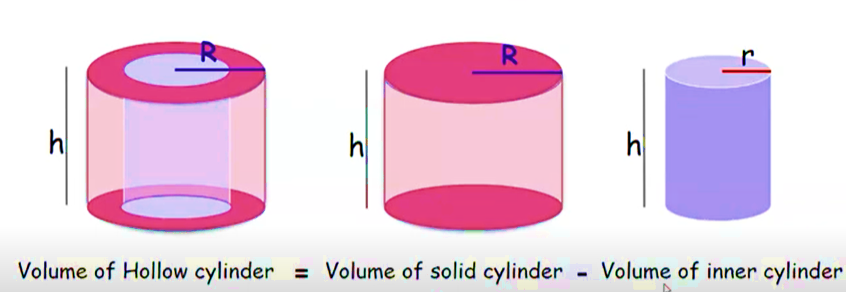
Formula for Hollow Cylinder  

As hollow cylinders contain both inner and outer surfaces, their volume can be calculated as the difference between their two volumes; their outer volume minus their inner one being defined as R minus r, with height h being their radiuses; their volume formula being

\(V = \pi (R^2 - r^2)h\)  

Calculations is of paramount importance in areas like engineering design and pipeline structures. This methodology holds great sway when making engineering designs or pipeline structures decisions.

Volume Formulas for Other Types of Cylinders

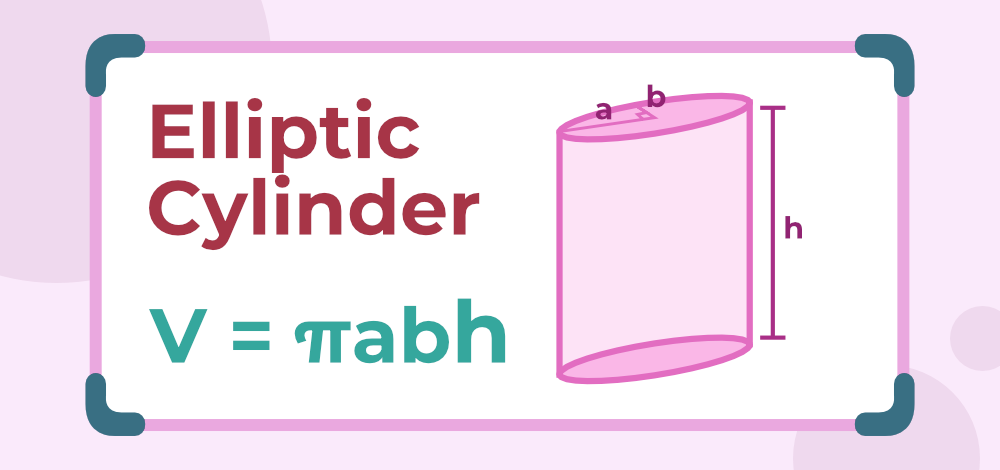
Practical applications often necessitate special formulae to accommodate unique scenarios, like an inclined cylinder where its base and lateral surface no longer meet at perpendicular lines; although volume calculation still depends on the base area and height calculations, geometric projection methods might need to be combined in order to solve it effectively. When its base forms an ellipse, its area is calculated using 

\(A = \pi ab\)  

(with a and b being the major and minor semi-axes, respectively), and the volume is  

\(V = \pi ab h\) 

They provide the mathematical support to effectively handle nonstandard cylindrical forms.

Converting Diameter to Radius  

Converting from diameters to radii is sometimes required in calculations; here is the formula. The equation

\(r = \frac{d}{2}\)  

applies not only to right circular but also hollow and special base shape cylinders and is an indispensable precursor of calculation.

Calculation Steps  

Calculating the volume of a cylinder involves taking several steps:

1. Determine whether it should be right, hollow, or special shape as per problem requirements.

2. To maintain consistent data for analysis.

3. Calculate the base area or difference in areas using an established formula.

4. To obtain volume, multiply base area times height. mes

5. When necessary, be mindful to adhere to consistent methods for unit conversion for accurate results.

By following these steps, one can master various methods for calculating cylinder volumes while also being able to apply them with flexibility when solving practical problems.

After mastering the above steps, next, try to calculate the volume of the cylinder yourself! If you still have questions, you can ask our AI assistant!

Other Related Properties and Applications

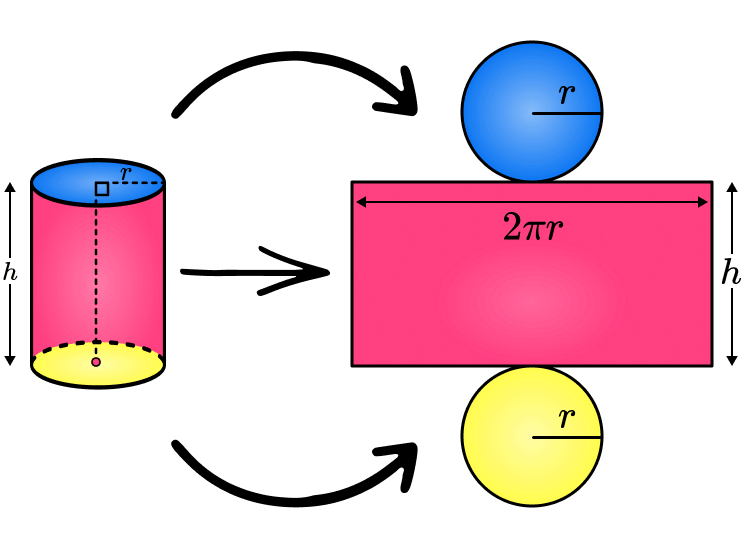
Surface Area of a Cylinder and its Formulas  

Not unlike volume, the surface area of a cylinder serves as another important metric to describe its geometric properties. A right circular cylinder's surface area comprises two distinct parts - an area of two bases and lateral surface areas. The area of a circle is given by  

\(A_{\text{circle}} = \pi r^2\)  

Therefore, the total area of the two bases is  

\(A_{\text{bases}} = 2\pi r^2\)  

Once unwrapped, the lateral surface can be seen to form a rectangle with length equaling\(2\pi r\) and width equivalent to height h; its area corresponds to

\(A_{\text{lateral}} = 2\pi r h\)  

Combining these parts, the total surface area formula for a right circular cylinder becomes evident.

\(A = 2\pi r^2 + 2\pi r h\)  

When working with hollow or open designs of cylindrical objects, surface area calculations must be calculated appropriately to suit any given situation. Mastery of these formulae and calculation methods not only helps engineers solve practical engineering design challenges more easily but can also facilitate more intuitive understanding of geometric figures composed from various parts.

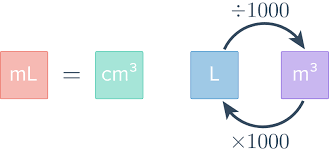
Volume Unit Conversions  

Practical applications require volume units to match engineering, chemical, or everyday data. Common units for volume conversion include cubic centimeters (cm3), cubic meters (m3), and liters (L). To illustrate, 1 cubic meter equals 1000 liters while one cubic centimeter equals one liter; this relationship can be expressed using equation

\(1\,\text{m}^3 = 1000\,\text{L} \quad,\quad 1\,\text{L} = 1000\,\text{cm}^3\)  

Attention should always be paid when converting units, with respect to both dimensioning consistency and the correct use of coefficients. For instance, when computing volume V of a certain cylinder in cubic centimeters; to convert into liters simply divide by 1000; similarly multiply 1000 to convert from cubic centimeters back into liters if need be. These conversions allow calculation results directly apply in practical scenarios like container capacity design and material proportioning.

Simply stated, whether calculating surface area meticulously or converting between volume units are two strategies which serve to bridge theory with practice by providing ease and accurate assurance when applying geometric knowledge in various fields.

Extensions and Comprehensive Applications

Mathematical Derivation: Geometric Proof of the Volume Formula  

From a geometric viewpoint, the volume formula for the right circular cylinder can be calculated through the summation method. Consider subdividing its height h into an infinite number of thin slices having infinitesimally small thickness and an area equivalent to that of its circular base, in this instance

\(\pi r^2\)  

Summing all of the slices' volumes enables us to arrive at an approximate total volume:

\(V = \int_0^h \pi r^2 \, dh = \pi r^2 h\)  

Calculus offers an intuitive method of derivation which clearly demonstrates the fundamental principle behind volume formulae, while at the same time providing mathematical tools necessary for dealing with non-uniform base areas or complex geometric bodies.

Real-Life Application Cases and Problem Solving  

Real-world applications of volume calculations of cylindrical objects are pervasive; when designing water tanks, designers must keep material costs under control while considering capacity needs and using volume formulas to quickly verify whether designs meet requirements; packaging industries leverage volumetric space optimization strategies to facilitate transportation while simultaneously cutting shipping costs; hollow cylinders used in mechanical structures or pipeline designs can use subtracting their inner cavity volumes for precise calculations, providing engineering safety assurances.

Interdisciplinary Discussion: Applications of Cylinder Volume in Engineering and Physics

Engineering studies the volume of cylindrical equipment such as oil tanks and generator units directly correlate with its capacity design, while, in physics, issues related to liquid containers' capacities, heat conduction, and compressibility calculations often feature prominently. By using theoretical research together with experimental data for simulation and prediction purposes, researchers can more efficiently simulate and predict system performance while encouraging in-depth discussions among diverse fields on volume-related parameters, leading to materials research for optimization techniques as well as providing foundations to combine economic efficiency with scientific accuracy for successful engineering applications.

Overall, this section expands not only upon the mathematical derivations of geometric volume calculations but also provides real-life examples and interdisciplinary analyses that demonstrate its wide applications across fields - offering an appealing blend of theory with practice.

This article begins by exploring basic geometric concepts and then progresses on to explain various cylinder volume formulas with detailed explanations. Based on real-life examples and engineering practices, this content emphasizes mathematical derivations as an essential building block in multidisciplinary applications and practices. Furthermore, readers will experience both theoretical depth as well as practical interest, creating an enriching learning experience for them all!

reference:

https://en.wikipedia.org/wiki/Cylinder

https://en.wikipedia.org/wiki/Right_circular_cylinder

https://en.wikipedia.org/wiki/Surface_area