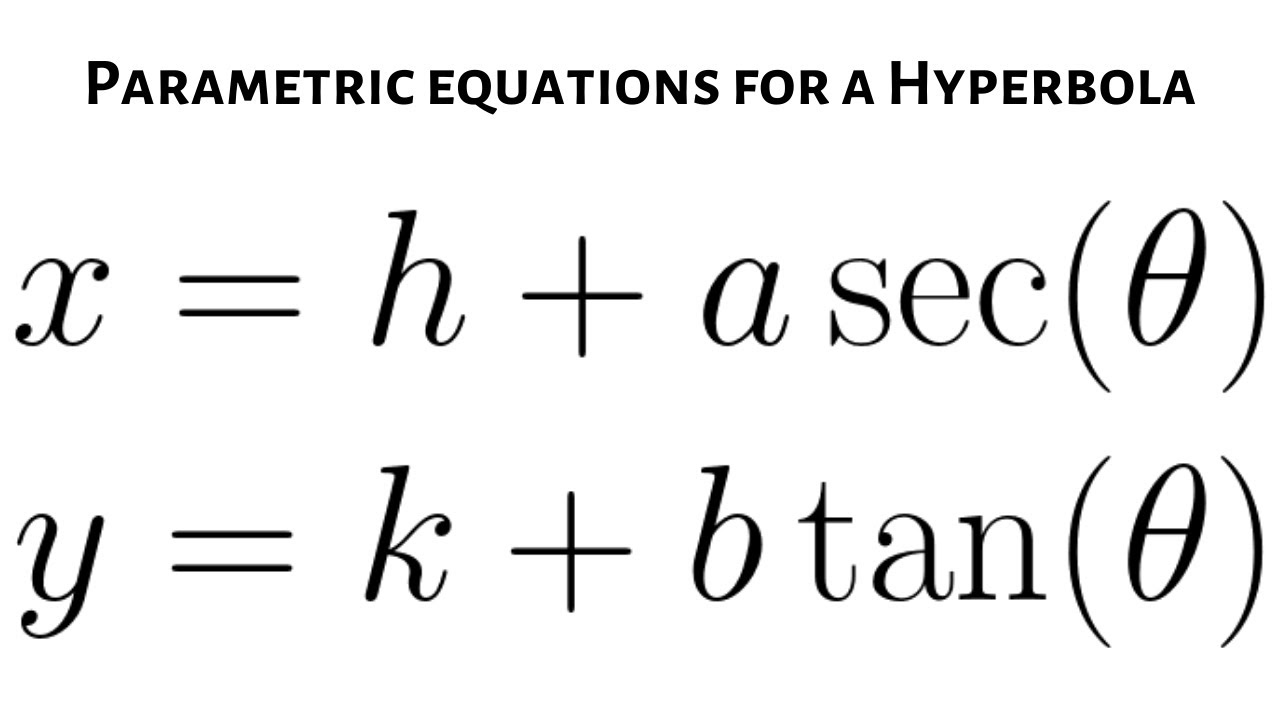¿Qué es una hipérbola?
¡Sumérgete en el mundo de las hipérbolas! Explora sus definiciones, propiedades, ecuaciones y cómo se aplican en la ingeniería, la ciencia espacial y la tecnología moderna.
La vida cotidiana contiene hipérbolas que pueden parecer desconocidas o distantes; por ejemplo, el movimiento celestial cuando las naves espaciales pasan cerca de la Tierra. Los diseños arquitectónicos de muchos puentes también utilizan principios del diseño de hipérbolas como su piedra angular. Esta curva especial no solo tiene un profundo significado matemático, sino que impregna gran parte de lo que damos por sentado cada día.
Las hipérbolas son secciones cónicas únicas con aplicaciones geométricas y prácticas fascinantes, que han cautivado a los estudiosos durante décadas. Pero, ¿qué son exactamente las hipérbolas y cuáles son su definición, propiedades, ecuaciones y usos? Ahora vamos a profundizar desglosándolas paso a paso para desvelar todos sus misterios.
Visión General de las Hipérbolas
¿Qué es una Hipérbola?
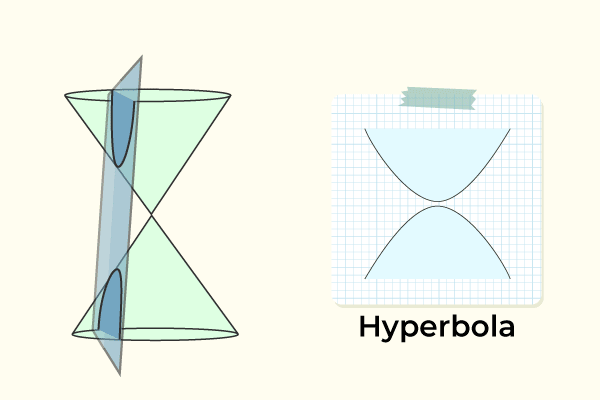
Las hipérbolas son secciones cónicas compuestas por intersecciones de planos y conos dobles. Geométricamente, una hipérbola se forma cuando un plano intersecta ambas hojas de una superficie cónica en un ángulo agudo respecto a su eje sin pasar por su vértice; la geometría analítica considera esta característica como fundamental para cualquier hipérbola: cualquier punto en ella con dos puntos fijos llamados focos permanece dentro de una diferencia absoluta de una constante de distancia entre puntos en ella y estos focos.
Las hipérbolas son figuras geométricas singulares, cada una compuesta de dos ramas simétricas que se extienden indefinidamente mientras se aproximan asintóticamente a ciertas líneas (las asíntotas) sin cruzarlas nunca. Su diseño intrincado proporciona la base para posteriores análisis matemáticos y aplicaciones prácticas.
Aplicaciones de las Hipérbolas
Las propiedades geométricas de las hipérbolas las hacen altamente valiosas en varias aplicaciones, desde cálculos científicos de órbitas de naves espaciales hasta tecnologías de comunicación y diseños de telescopios. Cuando una nave espacial se acerca a un planeta a una velocidad extremadamente alta, su trayectoria puede a menudo parecerse a la de una hipérbola; este fenómeno se conoce comúnmente como efecto de tirachinas gravitacional. Las hipérbolas también juegan un papel esencial en la representación de la propagación de ondas electromagnéticas, así como en las propiedades reflectantes de la luz; haciéndolas componentes indispensables en tecnologías de comunicación y diseños de telescopios.
La ingeniería también utiliza hipérbolas en los diseños de puentes. Por ejemplo, los diseños de puentes en arco a menudo emplean estructuras hiperbólicas para maximizar el rendimiento de carga y asegurar la estabilidad general.
Definición y Componentes de una Hipérbola
Definición Básica
Las hipérbolas son construcciones matemáticas definidas geométricamente de la siguiente manera.
Diferencia Constante en Distancias a los Focos
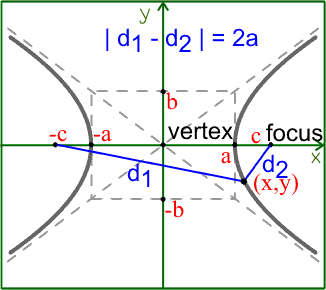
Las hipérbolas pueden definirse como conjuntos de puntos en un plano cuya diferencia absoluta con dos puntos fijos (llamados focos) permanece constante en el tiempo, expresado matemáticamente como:
\(|d_1 - d_2| = 2a\)
Donde \(d_1\) y \(d_2\) representan las distancias desde puntos en una hipérbola hasta sus focos y 2a es constante - distinguiendo así a las hipérbolas de otras secciones cónicas.
Simetría y Características de Trayectoria
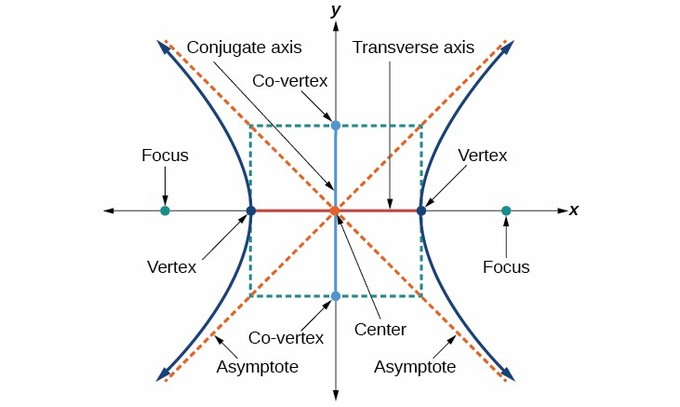
Las hipérbolas muestran una simetría geométrica única. Su punto central es simétrico mientras que contienen dos ejes perpendiculares (eje transverso y eje conjugado). Además, cada rama de la hipérbola se extiende en direcciones opuestas indefinidamente en ambas dimensiones formando líneas de trayectoria característicamente simétricas.
Componentes Geométricos
Para obtener un conocimiento exhaustivo de las hipérbolas, debemos examinar sus elementos geométricos primarios:
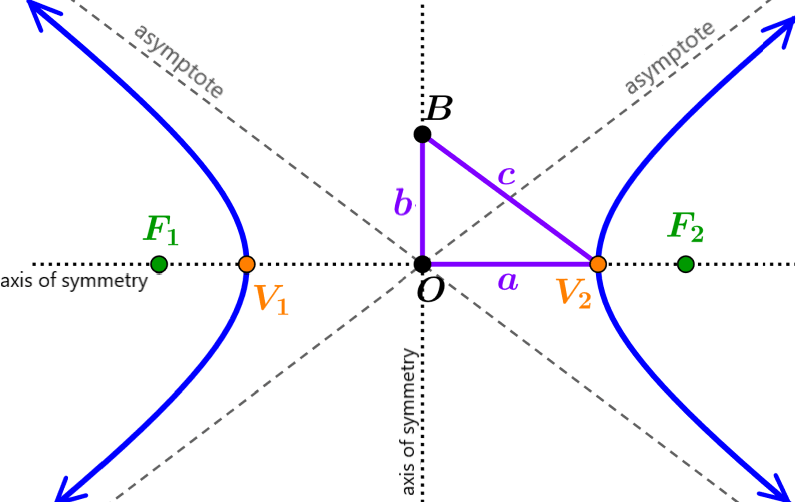
Vértices, Focos y Centro
Una hipérbola contiene dos vértices que conectan su eje transverso con sus bordes, dos focos que forman puntos fijos a lo largo de su curva, y su centro, ubicado a mitad de camino entre estos focos.
Eje Transverso y Eje Conjugado
El eje transverso se define como un eje perpendicular a ambos ejes conjugados que pasa a través del centro y define la dirección principal en la que se abre la hipérbola. Por el contrario, los ejes conjugados determinan el ancho de las ramas.
Asíntotas, Directrices y Latus Rectum
Las asíntotas de las hipérbolas son líneas rectas a las que las ramas se aproximan infinitamente pero nunca tocan, mientras que las directrices sirven como líneas auxiliares relacionadas con los focos y definen su geometría. Un latus rectum representa otra característica geométrica significativa al ser perpendicular al eje transverso mientras pasa por el/los foco(s).
Ecuaciones y Derivación de una Hipérbola
Ecuaciones Estándar y Clasificación
Ecuaciones de hipérbolas son ampliamente conocidas en geometría analítica y frecuentemente se expresan usando formas estándar. Las hipérbolas pueden dividirse en dos grupos principales dependiendo de dónde se encuentren sus focos:
Hipérbolas con Focos en el eje x o y
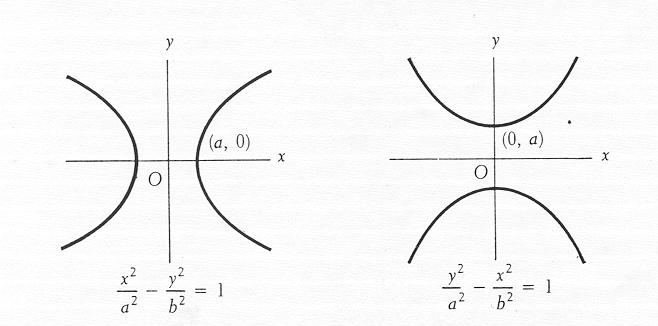
1. Hipérbolas con focos en el eje x:
Cuando los focos de una hipérbola están ubicados en el eje x, su ecuación estándar es:
\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\)
Aquí, \(2a\)) es la longitud del eje transversal; \(2b\) es su contraparte conjugada; los focos están ubicados en \((\pm c, 0)\),; por lo tanto, la relación \(c^2 = a^2 + b^2\) se mantiene cierta.
2. Hipérbolas con focos en el eje y:
Cuando ambos focos están ubicados a lo largo del eje y, la ecuación estándar para las hipérbolas se convierte en:
\(\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\)
Al igual que con los ejes principales, \(2a\) representa la longitud y \(2b\) su ancho respectivamente; los focos de esta curva se encuentran en cero en el punto \((0, \pm c)\) bajo la condición de que \(c^2 = a^2 + b^2\).
Hipérbolas Rectangulares
Una hipérbola rectangular es un caso especial de hipérbola donde las longitudes de ambos ejes transversales son iguales a las longitudes de los ejes conjugados (\(a = b\)). Así, su ecuación estándar se simplifica a:
\(\frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 \quad \text{o simplemente} \quad x^2 - y^2 = a^2\)
Las hipérbolas rectangulares tienen propiedades geométricas distintivas, incluyendo asintotas que siempre se intersecan de manera perpendicular y una solución más fácil al realizar análisis algebraicos y geométricos.
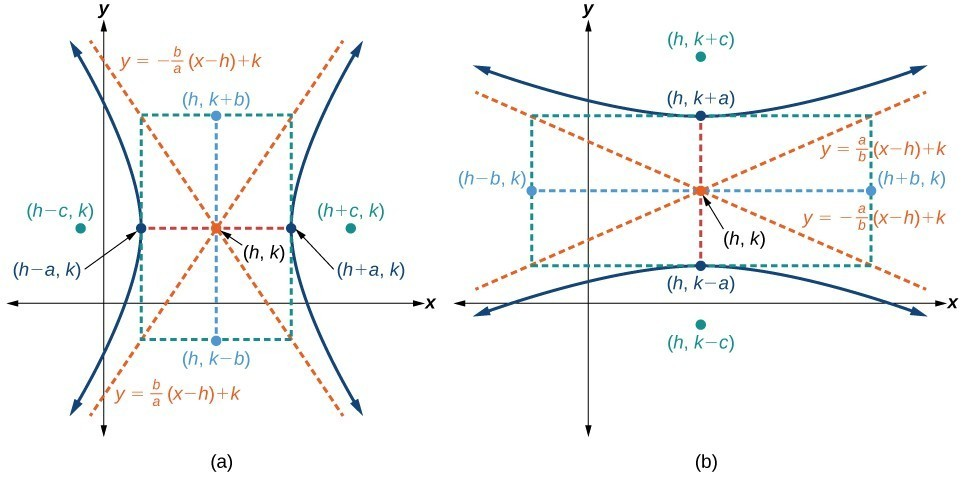
Ecuaciones Transladadas y Rotadas de una Hipérbola
En ocasiones, necesitamos desplazar o rotar una hipérbola lejos de su origen; para acomodar tales desplazamientos y rotaciones, utilizamos formas traducidas y rotadas de su ecuación:
1. Hipérbolas Transladadas:
Si desplazamos el centro de una hipérbola de \((0, 0)\) a una nueva posición \((h, k)\) entonces su ecuación estándar se convierte en:
\(\frac{(x - h)^2}{a^2} - \frac{(y - k)^2}{b^2} = 1\)
Esta forma puede aplicarse a hipérbolas cuyos centros se encuentran en cualquier coordenada.
2. Hipérbolas Rotadas:
Las hipérbolas rotadas pueden ser particularmente útiles en áreas de aplicaciones geométricas y físicas donde la rotación por un ángulo \(\theta\) requiere que su ecuación refleje esta transformación al sustituir las coordenadas rotadas en su ecuación original, manteniendo todas las características esenciales mientras se vuelve más compleja que su contraparte no rotada. Las hipérbolas rotadas ofrecen una considerable versatilidad.
Propiedades de una Hipérbola
Definición y Ecuación de las Asíntotas
Las asíntotas de una hipérbola son líneas que las ramas se acercan infinitamente pero nunca intersectan, actuando como líneas de referencia geométricas que definen tanto su simetría como su forma.
Para la hipérbola dada por la ecuación \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\), sus asíntotas son:
\(y = \pm \frac{b}{a} x\)
De manera similar, para la hipérbola \(\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\), las asíntotas son:
\(y = \pm \frac{a}{b} x\)
Las asíntotas son líneas rectas que definen hacia dónde se extienden las ramas de una hipérbola en dos dimensiones y también sirven para describir su forma y orientación general, ofreciendo ayuda visual al graficar o analizar esta forma.
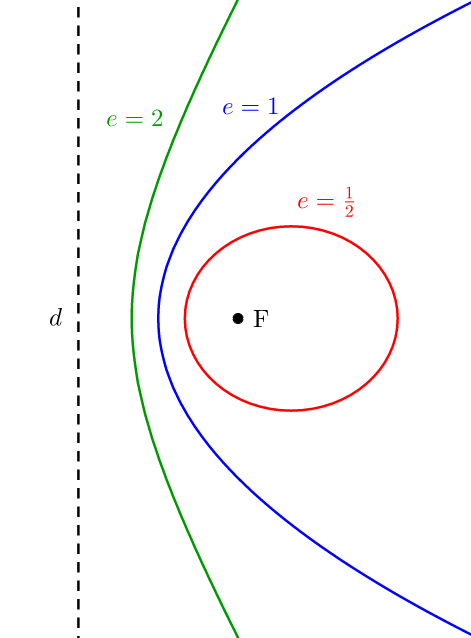
Significado y Fórmula de la Excentricidad
La excentricidad (\(e\)) es un parámetro esencial que mide la forma de las hipérbolas. Se puede definir como la relación entre la distancia entre los focos (\(c\)) y la longitud del semieje mayor (\(a\)):
\(e = \frac{c}{a} \quad \text{donde} \quad e > 1\)
Una excentricidad mayor a 1 indica que ambas ramas de una hipérbola presentan aperturas más amplias y parecen más planas; por el contrario, excentricidades menores indican ramas más afiladas y compactas. Una condición definida como \(e > 1\)diferencia a las hipérbolas de secciones cónicas similares como elipses (\(e < 1\)) o parábolas(\(e = 1\)).
Simetría y Características de la Imagen
Las hipérbolas muestran varias formas de simetría:
1. Simetría Central: Las hipérbolas presentan simetría central. Cada punto en su hipérbola tiene un punto opuesto a través de su centro que lo refleja exactamente.
2. Simetría Axial: Las hipérbolas son fáciles de clasificar y analizar gracias a su fuerte simetría axial. Comparten ejes transversales y conjugados, lo cual facilita el cálculo de estas curvas hiperbólicas.
Una imagen de una hipérbola representa dos ramas que se reflejan mutuamente y se conectan en un punto de inflexión, cada una comenzando desde un vértice y extendiéndose hacia su respectiva asíntota, creando las curvas abiertas características de las hipérbolas.
Hipérbolas Especiales: Hipérbolas Rectangulares
Las hipérbolas rectangulares son una subclase exclusiva de hipérbolas en la que tanto el eje transversal como el conjugado miden igual longitud (\(a = b\)). Su ecuación estándar se puede escribir como:
\(\frac{x^2}{a^2} - \frac{y^2}{a^2} = 1 \quad \text{o simplificada como} \quad x^2 - y^2 = a^2\)
Las asíntotas de una hipérbola rectangular siempre son perpendiculares, dadas por:
\(y = \pm x\)
Este tipo de hipérbola es fácil de trabajar tanto algebraica como gráficamente, haciéndola popular en aplicaciones prácticas, incluyendo transmisión de señales y reflexiones ópticas, debido a su simplicidad geométrica y simetría.
Representación Paramétrica y Gráficas de una Hipérbola
Ecuaciones Paramétricas de una Hipérbola
Las ecuaciones paramétricas ofrecen un medio eficiente de representar puntos en curvas al estudiar hipérbolas, eliminando la necesidad de resolver ecuaciones algebraicas y proporcionando una representación intuitiva. Cuando se aplica a ecuaciones hiperbólicas estándar como: \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\), las ecuaciones paramétricas aparecen como:
\(x = a \sec\theta \quad \text{y} \quad y = b \tan\theta\)
Aquí, \(\theta\) sirve como un parámetro, representando el ángulo formado entre cualquier punto en una hipérbola y los ejes transversales a través del eje focal. Estas ecuaciones paramétricas permiten que cualquier punto \((x, y)\) en cualquier hipérbola se exprese directamente utilizando su valor de \(\theta\).
Además, para hipérbolas con sus focos ubicados a lo largo del eje y y descritas por la ecuación \(\frac{y^2}{a^2} - \frac{x^2}{b^2} = 1\), su representación paramétrica se convierte en:
\(y = a \sec\theta \quad \text{y} \quad x = b \tan\theta\)
La representación paramétrica no solo simplifica los cálculos, sino que es ampliamente utilizada para el trazado de gráficos y algoritmos numéricos que abordan hipérbolas, haciendo el análisis geométrico más eficiente en general.
Si aún tienes preguntas sobre ecuaciones paramétricas, no dudes en consultar nuestro tutor de IA. Ofrece un análisis experto para ayudarte a resolver problemas, mejorar tu eficiencia de aprendizaje y guiarte hacia el éxito.
Trazado y Análisis de una Hipérbola
Forma del Gráfico en la Forma Estándar
Los gráficos de hipérbolas consisten en dos ramas que son simétricamente relacionadas alrededor de ambos ejes transverso y conjugado. Con respecto a una ecuación tal como\(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\), para la cual el eje transverso es el eje horizontal, y las dos ramas se abren a lo largo de él. Los vértices de la hipérbola se encuentran en \((a, 0)\) y \((-a, 0)\).
Características clave del gráfico:
Dirección de Apertura: Dependiendo de si su eje focal es horizontal o vertical, las ramas de una hipérbola se abren a lo largo de sus ejes transverso o conjugado.
Comportamiento Asintótico: Cada rama se acerca pero nunca intersecta sus asintotas respectivas, creando una apariencia de expansión suave.
Estructura Simétrica: Cada rama presenta su contraparte reflejada para una perfecta simetría a través de los ejes o el centro.
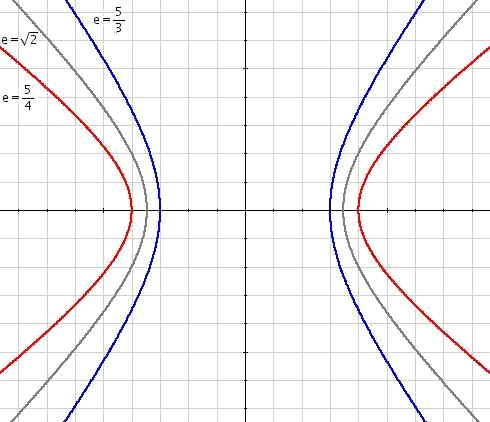
Rol de la Excentricidad en la Forma del Gráfico
La excentricidad(\(e\)) afecta directamente la forma del gráfico de una hipérbola. Cuando su excentricidad\(e\) está cerca de 1, sus ramas tienden a ser más empinadas y más cercanas entre sí, congregándose alrededor de su vértice. A medida que su excentricidad aumenta, sus ramas se abren más, volviéndose más planas a medida que más de sus ramas se separan y crean un patrón más plano de curvas.
La excentricidad puede tener varios impactos, incluyendo:
1. En un \(e \to 1\), las ramas de la hipérbola se asemejan a las curvas de una parábola.
2. En \(e \gg 1\), sus ramas se mueven casi paralelas a las asintotas para una curva más plana.
La excentricidad juega un papel integral en la definición de la geometría de las hipérbolas. Las variaciones en sus formas tienen importantes repercusiones para campos prácticos como la óptica y los sistemas de comunicación por satélite, donde su nivel de curvatura afecta directamente el rendimiento.
Aplicaciones de una Hipérbola
Aplicaciones en Ingeniería
Las hipérbolas han sido utilizadas durante mucho tiempo como un elemento de diseño en ingeniería. Sus propiedades geométricas han demostrado ser invaluables cuando se aplican a los diseños de puentes y estructuras; por ejemplo, algunos diseños de puentes de arco se inspiran en la forma curvilínea de la hipérbola; esto no solo resulta atractivo visualmente, sino que también distribuye eficazmente la presión mientras mejora la estabilidad y la capacidad de carga de las estructuras.
Las hipérbolas también han demostrado su valor en numerosos proyectos energéticos de gran magnitud, mostrando su uso práctico como elementos de diseño de torres de enfriamiento para plantas de energía nuclear. Su forma permite un flujo de aire eficiente, una disipación de calor óptima y estabilidad estructural, cualidades que benefician en especial al diseño de torres de enfriamiento para plantas nucleares. Los diseños hiperbólicos han resultado ser herramientas invaluables en la ingeniería industrial.
Aplicaciones en Ciencia
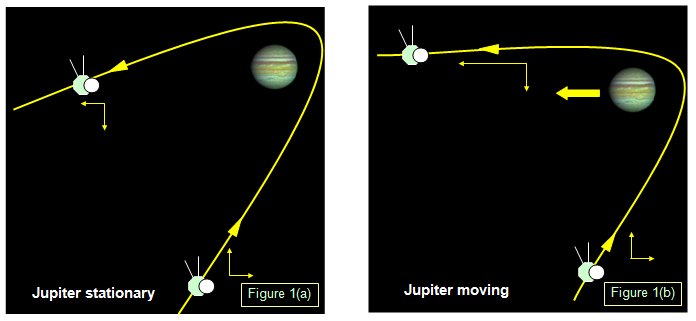
Las hipérbolas tienen muchas aplicaciones dentro de la ciencia, particularmente en física y astronomía. Cuando las naves espaciales encuentran el tirón gravitacional de cuerpos celestes, su trayectoria a menudo sigue una curva hiperbólica conocida como el efecto de la catapulta gravitacional; al aprovechar este fenómeno eficientemente, pueden cambiar rápidamente de velocidad y dirección con un uso mínimo de combustible, abriendo posibilidades para exploraciones interestelares a larga distancia.
Las hipérbolas han sido utilizadas durante mucho tiempo por sus propiedades focales para diseñar espejos y sistemas de antenas de alta precisión, tales como platos de radar o receptores satelitales; su capacidad efectiva para reflejar o enfocar la luz eficientemente lleva a tecnologías de comunicación mejoradas, así como dispositivos de observación.
Las hipérbolas también juegan un rol integral en la electrónica, particularmente en la creación de circuitos de filtros. Sus propiedades matemáticas ayudan a diseñar métodos efectivos de separación de frecuencias para satisfacer las especificaciones y necesidades del procesamiento de señales.
Exploración Adicional
Comparación Entre Hipérbolas y Otras Secciones Cónicas
Similitudes y Diferencias con Parábolas y Elipses
Las secciones cónicas comprenden elipses, parábolas e hipérbolas; su diferenciación generalmente puede determinarse mediante la excentricidad y las estructuras geométricas:
1. Diferencias en Excentricidad:
Elipses tienen una excentricidad (\(e\)) que satisface una condición de excentricidad menor que 1, lo que significa que la distancia entre los focos es menor que la longitud de su eje mayor.
Parábolas: La excentricidad es exactamente \(e = 1\), lo que significa que la distancia al foco es igual a la distancia desde la directriz.
Hipérbolas: La excentricidad debe satisfacer \(e > 1\)como se definió anteriormente, y la distancia entre los focos excede la longitud del eje transversal.
2. Diferencias en Estructuras Geométricas:
Las elipses forman curvas cerradas que son simétricas alrededor de ambos ejes, y las parábolas tienen una curva abierta que se extiende infinitamente en una dirección.
Las hipérbolas consisten en dos ramas abiertas conectadas por dos ramas simétricas que se extienden infinitamente en direcciones opuestas mientras se aproximan asintóticamente a ciertas líneas de referencia (asíntotas).
Al comparar estas propiedades, se puede entender que las hipérbolas se destacan entre las secciones cónicas debido a sus dos ramas y una excentricidad que excede 1.
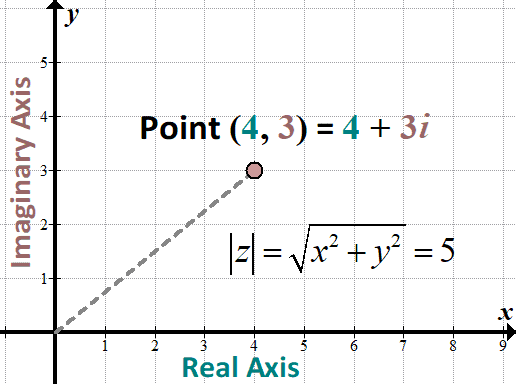
Hipérbolas en el Plano Complejo
Ecuaciones de Hipérbola en el Plano Complejo
Las hipérbolas pueden representarse en el plano complejo utilizando números complejos, lo que facilita el análisis de rotaciones y transformaciones. Una ecuación hiperbólica como \(\frac{x^2}{a^2} - \frac{y^2}{b^2} = 1\) puede expresarse mediante el formato de números complejos como sigue.
\(z \cdot \overline{z} = 1 + \left(\frac{y}{b}\right)^2\)
donde \(z = x + iy\). Esta representación amplía nuestro estudio de las hipérbolas, proporcionando nuevas formas de verlas a través de espacios multidimensionales.
Representación Paramétrica y Significado Geométrico en el Plano Complejo
En el plano complejo, las hipérbolas también pueden parametrizarse usando variables complejas para facilitar transformaciones geométricas como traslaciones, rotaciones y reflexiones. Al delinear matemáticamente cálculos de posición y ángulo de curvas hiperbólicas en uso en campos de procesamiento de señales y modelado de imágenes.
La perspectiva avanzada de las hipérbolas ofrece importantes implicaciones en disciplinas donde los modelos matemáticos deben describir espacios complejos, permitiendo una exploración más profunda tanto de la teoría como de la práctica respecto a la geometría de la hipérbola.
Las hipérbolas desempeñan un papel indispensable tanto matemática como prácticamente, desde la definición geométrica hasta ecuaciones paramétricas y análisis de propiedades, desde implementaciones prácticas hasta sus aplicaciones. Su versatilidad es evidente dondequiera que se encuentren: exploración espacial, diseño de ingeniería e instrumentos científicos los usan con frecuencia aunque permanezcan herramientas invisibles pero esenciales; al estudiar las hipérbolas de manera integral, observamos su capacidad de combinar belleza con utilidad, desbloqueando un potencial inimaginable.
referencia:
https://en.wikipedia.org/wiki/Hyperbola