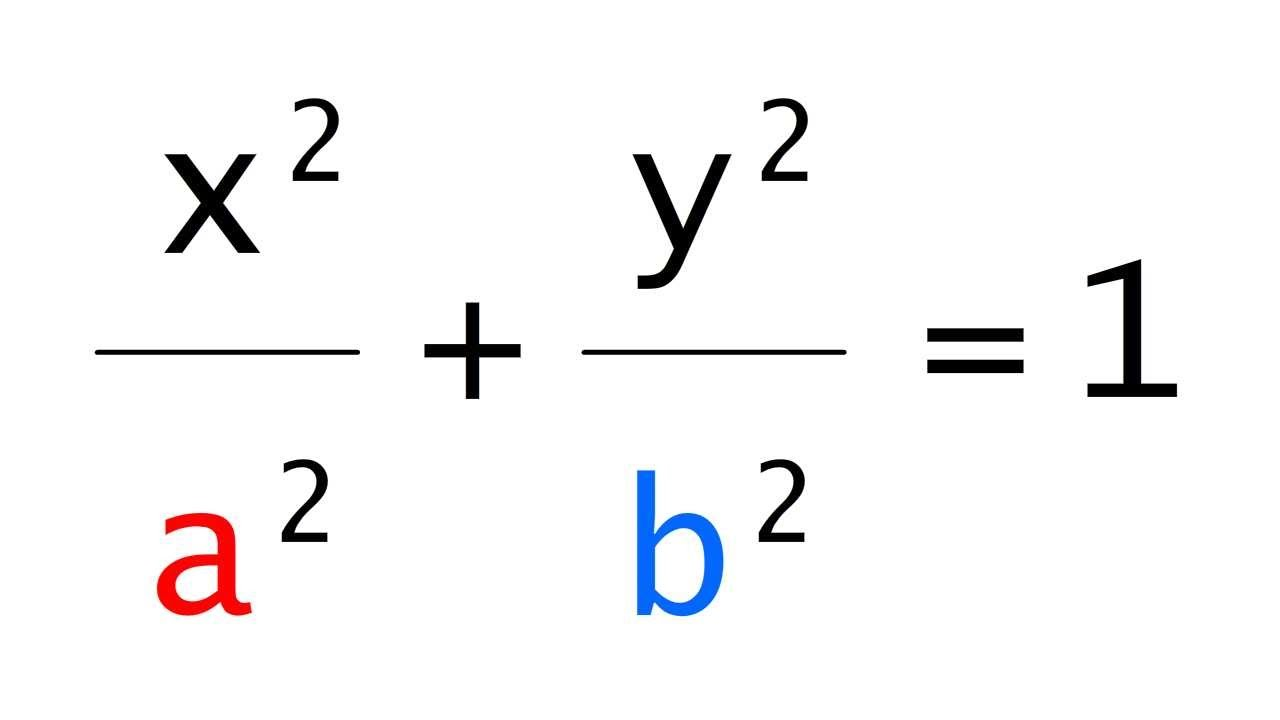¿Qué es una Elipse?

La matemática juega un papel integral en la vida cotidiana; desempeña un papel fundamental en la explicación de fenómenos naturales. Uno de esos eventos naturales que requiere matemáticas para explicarse es la sombra de objetos circulares, por lo que cuando una fuente de luz se inclina ligeramente, su sombra se transforma de circular a algo completamente único: una elipse. No solo se encuentran elipses ubicuamente en el arte y la arquitectura, sino que también tienen un papel esencial en la astronomía y la física. ¡Adentrémonos más en la comprensión de estas misteriosas pero ubicuas figuras geométricas a través de este artículo!

Definición y Características Básicas de una Elipse

Definición de Elipse

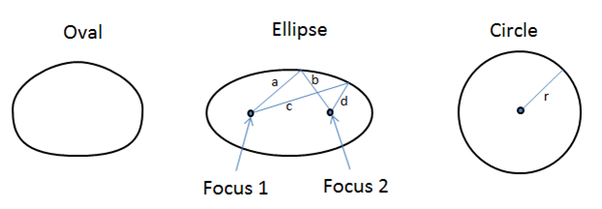
Una elipse es una figura geométrica definida por sus distancias constantes desde cualquier punto de su curva a dos puntos fijos conocidos como sus focos (Focos). En pocas palabras, consiste en todos los puntos en el plano que satisfacen esta condición única.

Matemáticamente, una elipse puede definirse de la siguiente manera: Dados dos puntos fijos \(F_1\) y \(F_2\) en un plano, cualquier punto \(P\) satisface la condición:

\(|PF_1| + |PF_2| = 2a \quad (a > |F_1 F_2|/2),\)

donde la trayectoria trazada por \(P\) es una elipse.

Formación de una Elipse

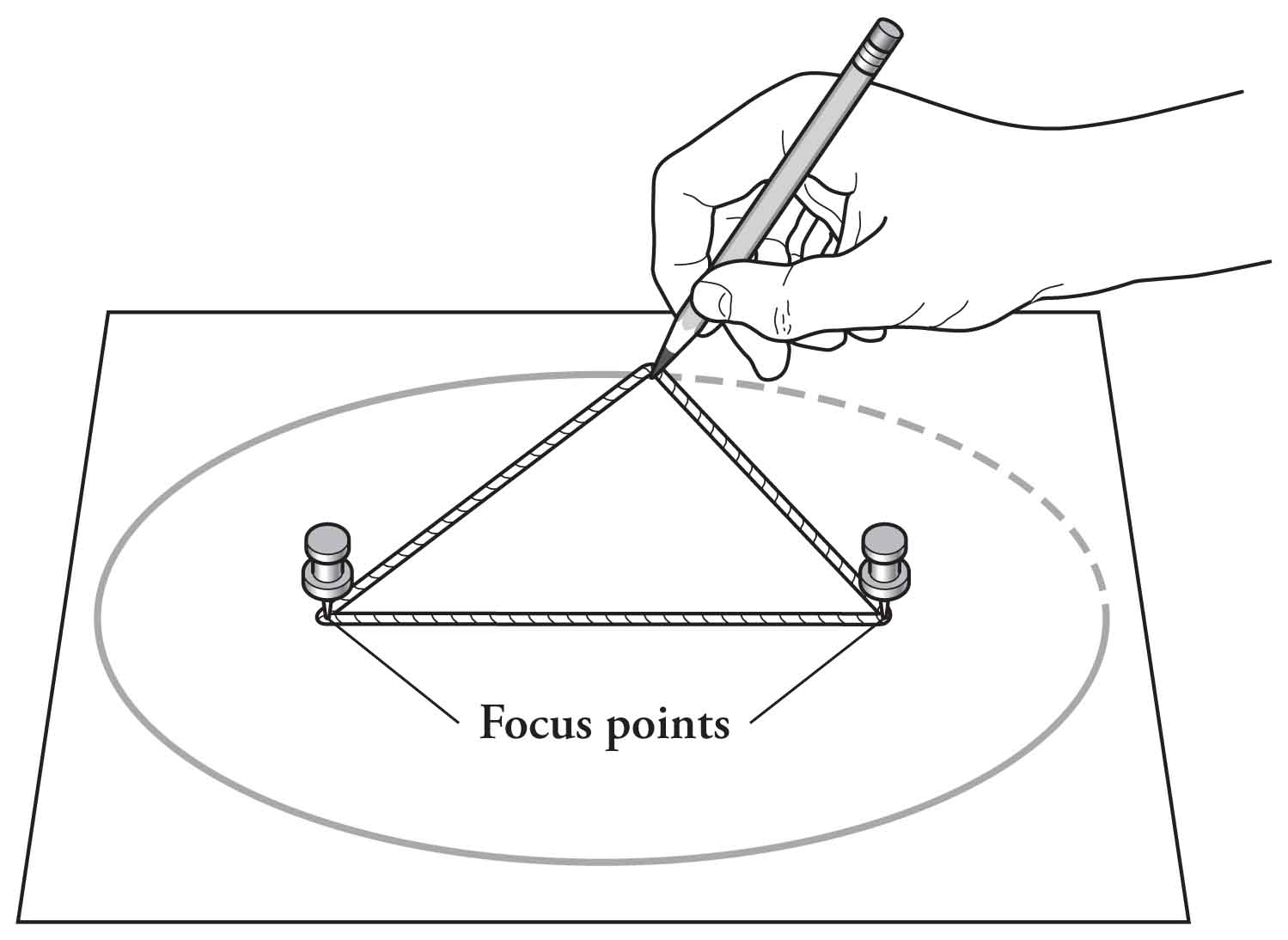
Una elipse puede formarse utilizando diversos medios. Una técnica popular implica fijar ambos extremos de una cuerda de longitud fija a los focos de una elipse, y al tensar con un lápiz conduce a la creación de la propiedad de distancia constante: Se revela una elipse.

\(|PF_1| + |PF_2| = 2a\)

Una elipse en geometría analítica está determinada por su intersección entre un cono y un plano inclinado en un ángulo menos empinado que sus respectivas alturas inclinadas del cono, llevándola a su clasificación como un tipo de "sección cónica".

Forma y Simetría de una Elipse

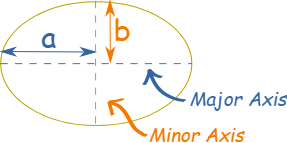
La forma de una elipse puede describirse por sus ejes mayor y menor:

- El eje mayor define el segmento de línea más largo a través de una elipse con una longitud aproximada de dos veces un radio (2a).

- El eje menor se encuentra perpendicular al eje mayor y representa el segmento de línea más corto a través de una elipse con una longitud de borde de (2b).

Una elipse exhibe simetría bilateral; su centro sirve como su punto de simetría.

- Las elipses son figuras geométricas caracterizadas por ser simétricas sobre ambos ejes mayor y menor, creando un equilibrio en su forma geométrica que enfatiza el equilibrio perfecto.

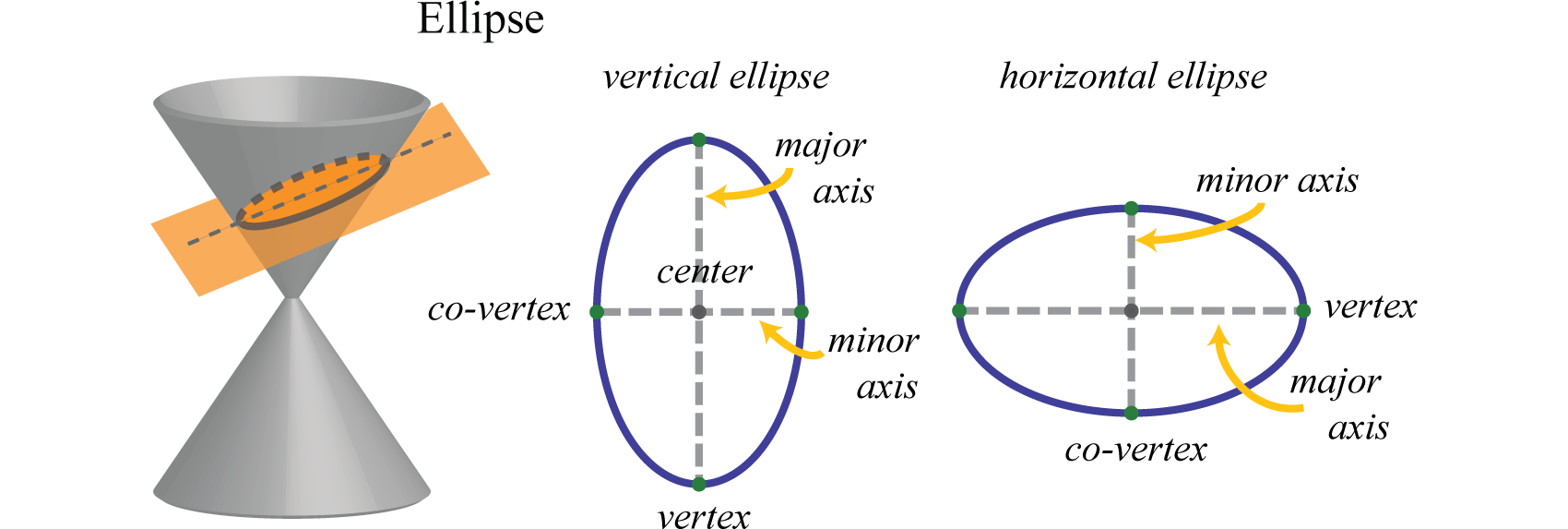
Elipses Horizontales y Verticales

Las elipses pueden dividirse en dos clases según la dirección de su eje mayor:

1. Elipse Horizontal (Eje Mayor a lo largo del \(x\)-eje):

\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \quad (a > b > 0)\)

2. Elipse Vertical (Eje Mayor a lo largo del \(y\)-eje):

\(\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1, \quad (a > b > 0)\)

Incluso cuando su dirección varía, sus propiedades geométricas fundamentales permanecen idénticas.

Componentes de una Elipse

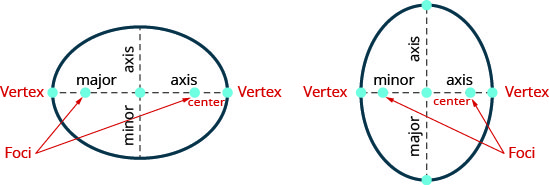
Focos

Los focos son uno de los elementos más críticos de una elipse. Dado que una elipse con longitudes de eje mayor y menor de 2a y 2b, respectivamente, tiene la siguiente forma, su distancia entre focos puede expresarse de la siguiente manera.

\(c = \sqrt{a^2 - b^2}, \quad (a > b).\)

Las coordenadas de los dos focos \(F_1\) y \(F_2\)son:  

- Para una elipse horizontal: \(F_1(-c, 0)\) y \(F_2(c, 0)\).  

- Para una elipse vertical: \(F_1(0, -c)\) y\(F_2(0, c)\).  

Los focos determinan la forma y geometría de una elipse adhiriéndose a su propiedad clave:

\(|PF_1| + |PF_2| = 2a,\)

Donde \(P\) es cualquier punto en la elipse.

Centro

El centro marca el punto de intersección entre los ejes mayor y menor y sirve como el centro de simetría de una elipse. Sin embargo, al trabajar con ecuaciones en forma estándar simplificadas en geometría analítica, el centro actúa como un punto de referencia, como cuando se resuelven ecuaciones estándar utilizando formas estándar de ecuaciones simplificadas.

- Para elipses horizontales, las coordenadas del centro son ya sea \((0, 0)\) o \((h,k)\) si están desplazadas de sus ubicaciones originales (el origen).

Esta herramienta ayuda a derivar y calcular parámetros de elipses horizontales.

Vértices y Directriz

- Vértices: Estos son los extremos del eje mayor.  

- Para una elipse horizontal: \((a, 0)\) y \((-a, 0)\).  

- Para una elipse vertical: \((0, a)\) y \((0, -a)\).  

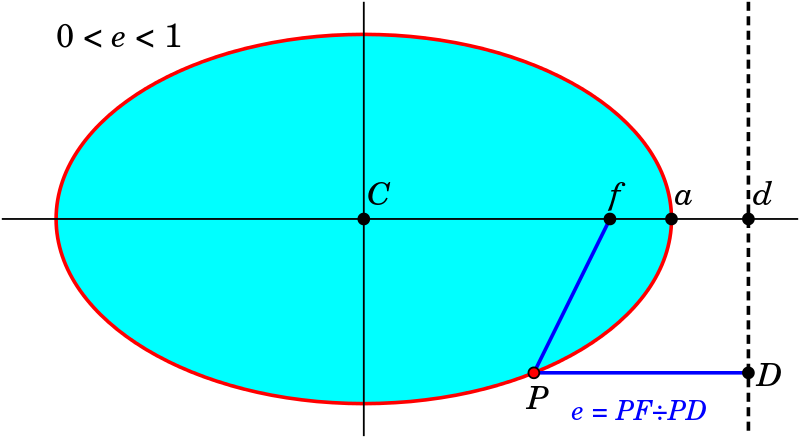
- Directriz: Una directriz es una línea auxiliar relacionada con el foco que define su relación con una elipse:

- Para una elipse horizontal:  

\(x = \pm \frac{a}{e}, \quad e = \frac{c}{a}.\)

- Para una elipse vertical:  

\(y = \pm \frac{a}{e}, \quad e = \frac{c}{a}.\)

Aquí, \(e\) representa la excentricidad de la elipse.

Ejes Mayor y Menor

El eje mayor de una elipse se define como su diámetro más largo entre ambos focos.

\(\text{Longitud del Eje Mayor} = 2a.\)

Por el contrario, el eje menor es el diámetro más corto, perpendicular al eje mayor:  

\(\text{Longitud del Eje Menor} = 2b.\)

Ejes Transversal y Conjugado

- El eje transversal se refiere al eje mayor, enfatizando la simetría y estructura de una elipse.

El eje conjugado se refiere a su eje menor más corto para una mejor comprensión geométrica de una elipse.

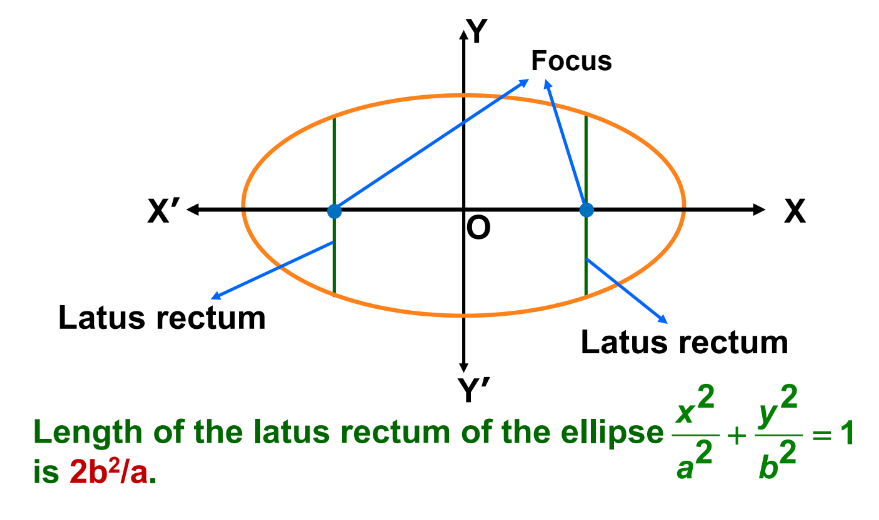
Latus Rectum

Un "latus rectum" (segmento de línea perpendicular al eje mayor que pasa por un foco) se define por:

\(\text{Longitud del Latus Rectum} = \frac{2b^2}{a}.\)

Esta propiedad es especialmente esencial en análisis ópticos y geométricos.

Ecuaciones de la Elipse y Derivación

Forma Estándar de la Ecuación de la Elipse

La forma estándar de una ecuación de elipse proporciona los medios para describir sus propiedades geométricas. Dependiendo de la dirección en la que apunte su eje mayor, existen dos formas para esta ecuación:

1. Elipse Horizontal (Eje mayor a lo largo del \(x\)-eje)  

\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \quad (a > b > 0)\)

Aquí:  

- \(a\): Semi-eje mayor (paralelo al \(x\)-eje);  

- \(b\): Semi-eje menor (paralelo al \(y\)-eje);  

- \(c = \sqrt{a^2 - b^2}\): Distancia desde el centro a cada foco;  

- Focos: \((-c, 0)\) y \((c, 0)\).  

2. Elipse Vertical (Eje mayor a lo largo del \(y\)-eje)  

\(\frac{x^2}{b^2} + \frac{y^2}{a^2} = 1, \quad (a > b > 0)\)

Aquí:  

- \(a\): Semi-eje mayor (paralelo al \(y\)-eje);  

- \(b\): Semi-eje menor (paralelo al \(x\)-eje);  

- \(c = \sqrt{a^2 - b^2}\): Distancia desde el centro a cada foco;  

- Focos: \((0, -c)\) y \((0, c)\).

Ecuación en Forma General

Una forma estándar para una ecuación de elipse puede generalizarse en esta forma:

\(Ax^2 + By^2 + Cx + Dy + E = 0, \quad (A > 0, B > 0),\)

Donde las constantes A, B, C, D y E son constantes, esta forma general puede reducirse a la forma estándar a través de transformaciones como completar el cuadrado.

Ecuación Paramétrica

Las ecuaciones paramétricas ofrecen otro método para representar una elipse: ofrecen representaciones dinámicas. Un ejemplo sería una elipse con su centro en (0, 0); esto daría:

1. Elipse Horizontal:

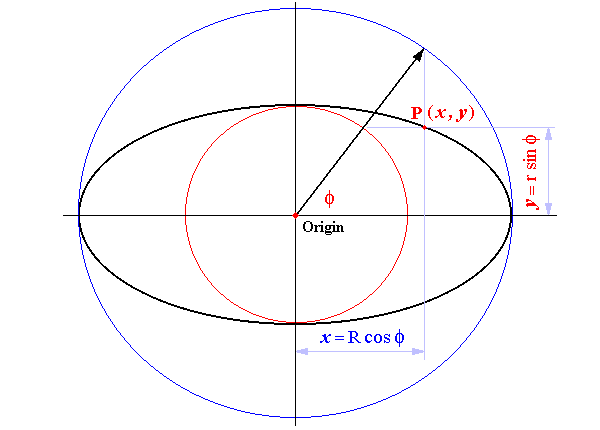
\(x = a \cos\theta, \quad y = b \sin\theta, \quad \theta \in [0, 2\pi]\)

2. Elipse Vertical:

\(x = b \cos\theta, \quad y = a \sin\theta, \quad \theta \in [0, 2\pi]\)

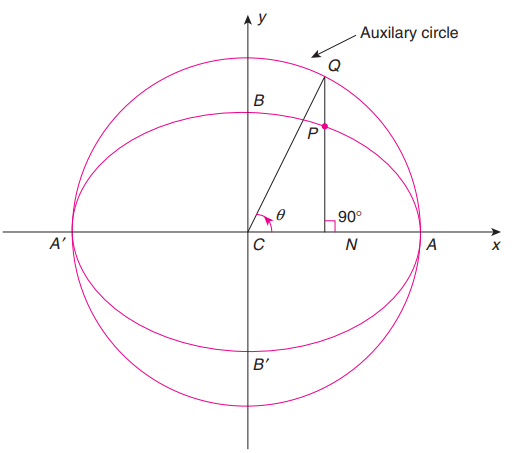
Aquí, \(\theta\) representa el ángulo entre la línea que conecta \(P(x, y)\) al centro de la elipse y el eje \(x\)-positivo de la elipse. Esta parametrización puede ser especialmente útil para trazar o calcular dinámicamente puntos en la superficie de una elipse.

La Derivación de la Ecuación de la Elipse

La derivación de una ecuación de elipse sigue su definición geométrica: la suma de las distancias desde cualquier punto en la curva hasta ambos focos es constante. Aquí está cómo se hace:

1. Dado que los focos de una elipse se encuentran en \((-c, 0)\) y \((c, 0)\), cualquier punto \(P(x, y)\) en ella debe satisfacer:

\(|PF_1| + |PF_2| = 2a.\)

2. Expande los términos de distancia:

\(\sqrt{(x + c)^2 + y^2} + \sqrt{(x - c)^2 + y^2} = 2a.\)

3. Cuadra ambos lados y simplifica usando álgebra, dando como resultado:

\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1, \quad \text{donde } b^2 = a^2 - c^2.\)

Esto confirma la forma estándar de una ecuación de elipse aplicable tanto a elipses horizontales como verticales.

Propiedades de una Elipse

Excentricidad de la Elipse

La excentricidad (abreviada "\(e\)") es una medida numérica de la forma de una elipse que la cuantifica mediante la razón entre la distancia entre los focos y la longitud del eje mayor. Este valor determina la excentricidad \(e\).

\(e = \frac{c}{a}, \quad (0 < e < 1),\)

donde \(c = \sqrt{a^2 - b^2}\).  

A \(e \to 0\), una elipse se aproxima a un círculo perfecto; a \(e \to 1\), sus dimensiones se vuelven más alargadas.

Suma Constante de Distancias a los Focos

Una característica importante de una elipse es que su suma de distancias desde cualquier punto\(P\) en ella a ambos focos \(F_1\) y \(F_2\)permanece constante e igual a \(2a\):

\(|PF_1| + |PF_2| = 2a.\)

La óptica se basa en gran medida en esta propiedad, ya que su explicación radica en la capacidad de los espejos y lentes elípticos para enfocar.

Círculo Auxiliar

Un círculo auxiliar para una elipse se define como cualquier círculo centrado en su centro con un radio igual al semieje mayor \(a\):

\(x^2 + y^2 = a^2.\)

Un círculo auxiliar ayuda a parametrizar una elipse y a estudiar sus propiedades geométricas.

Círculo Director

El círculo director es un concepto teórico utilizado en geometría avanzada. Se refiere al lugar geométrico de puntos desde los cuales las tangentes trazadas a una elipse son perpendiculares a su eje focal y tiene una ecuación:

\(x^2 + y^2 = a^2 + b^2.\)

Este círculo llama la atención sobre la relación entre la elipse y la simetría circular y tiene aplicaciones en diseños de sistemas ópticos.

Aplicaciones de una Elipse

Aplicaciones en Física e Ingeniería

Las elipses desempeñan un papel integral en varias disciplinas de la física y la ingeniería. Algunas aplicaciones clave de esta forma incluyen:

1. Diseño Óptico: Las elipses exhiben una propiedad reflectante única, en la que cualquier rayo de luz que emana de un foco se refleja en la superficie interna de la elipse y converge en el segundo foco. Esta propiedad es crucial en el diseño de reflectores elípticos, concentradores ópticos y dispositivos acústicos.

Por ejemplo, en un espejo elíptico, una fuente de luz colocada en un foco dirige todos los rayos reflejados para converger perfectamente en el otro foco, permitiendo una concentración precisa de luz o energía.

2. Estructuras de Puentes y Cúpulas: Tanto los puentes y cúpulas antiguos como los modernos emplean diseños elípticos para distribuir la carga de manera eficiente, lo que conduce a una mayor estabilidad bajo presión.

Ejemplos incluyen la Catedral de San Pablo en Londres y los anfiteatros romanos que utilizan arcos elípticos.

3. Movimiento Orbital y de Partículas: Las trayectorias elípticas a menudo resultan del estudio de movimientos de partículas y órbitas en física.

Las partículas cargadas que se mueven a través de un campo magnético uniforme pueden tomar una trayectoria elíptica en ciertas circunstancias.

Importancia en Astronomía

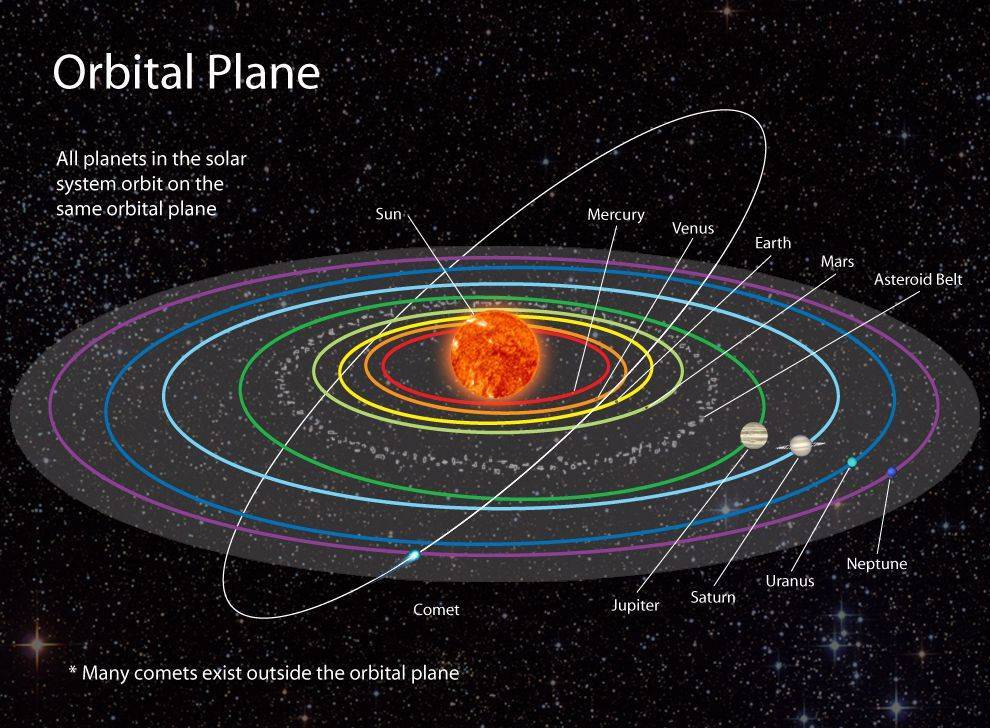
Las elipses juegan un papel integral en la astronomía, quizás mejor expresado por la Primera Ley del Movimiento Planetario de Kepler, que afirma:

La órbita de un planeta alrededor del Sol puede ser representada como una elipse con un foco como su punto central;

Aplicaciones específicas para Órbitas Planetarias incluyen:

1. Órbitas Planetarias: Las órbitas de la Tierra, Marte y otros planetas alrededor del Sol pueden aproximarse usando un modelo elíptico; sin embargo, sus excentricidades \(e\) tienden a ser bastante bajas, lo que significa que sus caminos a menudo son casi circulares.

Por ejemplo, la órbita de la Tierra presenta una excentricidad de aproximadamente 0.0167, haciendo su camino casi circular.

2. Trayectorias de Cometas: Las trayectorias de los cometas son muy diferentes de las trayectorias de los planetas en que sus excentricidades tienden a ser significativamente mayores, a menudo aproximándose a 1. Sus órbitas siguen elipses muy alargadas con excentricidades que se acercan a uno.

El cometa de Halley, por ejemplo, sigue una órbita elíptica.

3. Sistemas de Estrellas Binarias: Estos sistemas de estrellas binarias presentan dos estrellas que orbitan alrededor de su centro de masa común de manera elíptica - comprender esta característica es clave al estudiar dinámicas astrofísicas.

Ejemplos en el Mundo Real

Las elipses se pueden encontrar en todas partes en la vida cotidiana y sirven para una serie de usos prácticos:

1. Pistas Atléticas: Las pistas de atletismo estándar se asemejan a una forma elíptica al tener dos secciones rectas conectadas por semicírculos para aproximar su forma estéticamente mientras cumplen con las necesidades de eficiencia funcional. Esta estructura asegura un equilibrio estético mientras optimiza la eficiencia funcional.

2. Entrenadores Elípticos: Estas máquinas de ejercicio emplean movimientos similares a una trayectoria elíptica para minimizar el impacto en las articulaciones mientras ofrecen opciones de zancada natural que crean entrenamientos cardiovasculares efectivos.

3. Arte y Arquitectura: Las elipses son comunes en el diseño de jardines, esculturas y decoraciones debido a sus formas simétricas y atractivo visual. Lagos o fuentes en arquitectura paisajista a veces adoptan una forma elíptica para lograr armonía estética.

Fórmulas de la Elipse

Fórmula del Área

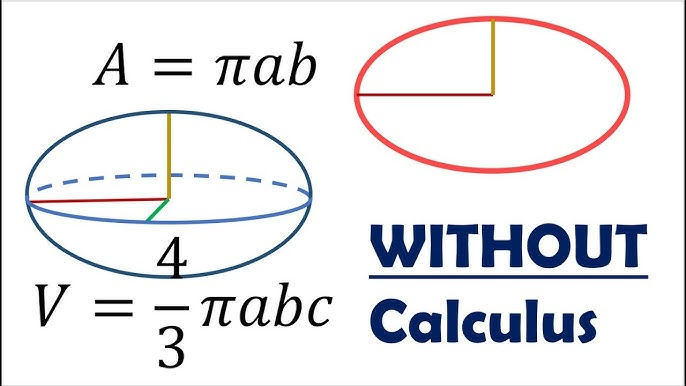
El área de una elipse se puede calcular usando sus ejes semi-mayor y semi-menor; su fórmula es la siguiente.

\(\text{Área} = \pi \cdot a \cdot b,\)

Donde:

- \(a\): Longitud del eje semi-mayor,  

- \(b\): Longitud del eje semi-menor,  

- \(\pi\): La constante matemática es aproximadamente 3.14159.

Esta fórmula se puede obtener mediante integración o comparando las proporciones de una elipse con las de un círculo.

Fórmula del Perímetro

Una fórmula aproximada conocida como la primera aproximación de Ramanujan a menudo puede proporcionar la solución:

\(\text{Perímetro} \approx \pi \cdot \left[ 3(a + b) - \sqrt{(3a + b)(a + 3b)} \right].\)

Para cálculos exactos, se puede usar una integral elíptica:

\(\text{Perímetro} = 4a \cdot \int_{0}^{\frac{\pi}{2}} \sqrt{1 - e^2 \sin^2\theta} \, d\theta,\)

donde \(e = \frac{c}{a}\) es la excentricidad de la elipse.

Fórmula del Latus Rectum

La longitud del latus rectum es una propiedad esencial de una elipse, especialmente en sus aplicaciones reflectantes y ópticas. La fórmula es:

\(\text{Longitud del Latus Rectum} = \frac{2b^2}{a}.\)

Esta medida es crucial en el estudio de órbitas elípticas y caminos ópticos.

Ecuaciones de la Tangente y la Normal

La longitud del latus rectum es una propiedad integral de una elipse, y sus aplicaciones reflectantes y ópticas incluyen reflexión. Para encontrar su fórmula:

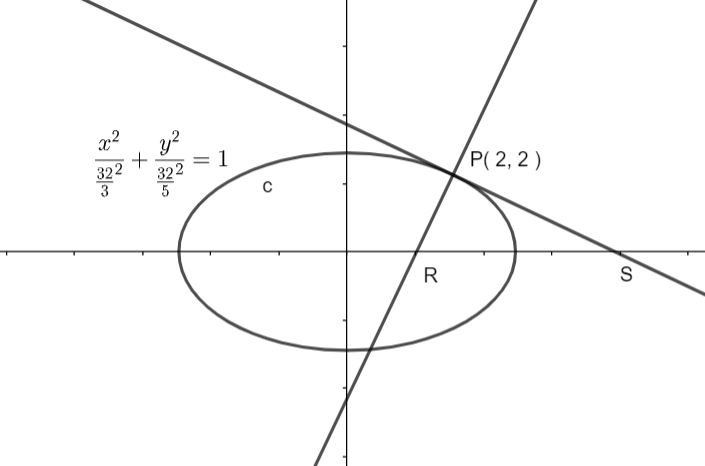
1. Ecuación de la Tangente:

- Para una elipse horizontal:

\(\frac{xx_1}{a^2} + \frac{yy_1}{b^2} = 1.\)

- Para una elipse vertical:

\(\frac{xx_1}{b^2} + \frac{yy_1}{a^2} = 1.\)

2.Ecuación de la Normal (Perpendicular a la Tangente): Para líneas normales, la pendiente es igual al recíproco negativo de su pendiente tangente; esta expresión también se puede escribir usando una derivada de la ecuación de una elipse como entrada.

Estas ecuaciones establecen una relación geométrica entre los puntos de una elipse y sus líneas adyacentes.

Análisis Comparativo de la Elipse y Otras Formas Geométricas

Diferencias Entre una Elipse y un Círculo

Una elipse y un círculo difieren principalmente en sus propiedades focales:

1. Un círculo puede considerarse como un caso extremo de una elipse en la que ambos focos convergen en un único punto (llamado su centro).

2. En una elipse, \(a > b\), mientras que para un círculo \(a = b = r\) (radio).  

- Ecuación de la elipse:  

\(\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1.\)

- Ecuación del círculo:  

\(x^2 + y^2 = r^2.\)

En general, los círculos demuestran una mayor simetría y la excentricidad \(e = 0\).

Relación Entre una Elipse y un Óvalo

Una elipse es una forma matemáticamente rigurosa; un óvalo se refiere más ampliamente a cualquier figura redonda y alargada con contornos redondeados que aproximan el perímetro de una elipse; algunos óvalos aproximan esta propiedad pero no cumplen con la propiedad de distancias de suma constante a los focos.

Comparación Entre Elipse e Hipérbola

Las elipses y las hipérbolas comparten similitudes como secciones cónicas con dos focos; sin embargo, sus propiedades varían considerablemente:

1. Definiciones:

- Elipse: La suma de las distancias a los dos focos es constante.

\(|PF_1| + |PF_2| = 2a.\)

- Hipérbola: La diferencia de las distancias a los dos focos es constante.

\(|PF_1| - |PF_2| = 2a.\)

2. Forma: Una elipse se define como una curva cerrada mientras que las hipérbolas son curvas abiertas con dos ramas, proporcionando aplicaciones distintivas tanto en física como en geometría.

Como figura geométrica esencial, una elipse simboliza tanto la elegancia matemática como la utilidad práctica. Desde el movimiento planetario en astronomía hasta la precisión en ingeniería óptica y estructuras, sus aplicaciones abarcan campos diversos. Investigamos la definición, componentes, propiedades de ecuaciones, así como la relevancia en la vida real de las elipses para este artículo. Con su mezcla de significación teórica e implicaciones en la realidad tangible, se erige como un pilar de la geometría como conexión entre la matemática abstracta y la realidad tangible.

referencia:

https://es.wikipedia.org/wiki/Elipse

https://es.wikipedia.org/wiki/Hip%C3%A9rbola

https://es.wikipedia.org/wiki/C%C3%ADrculo_director