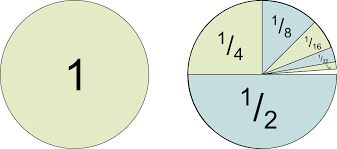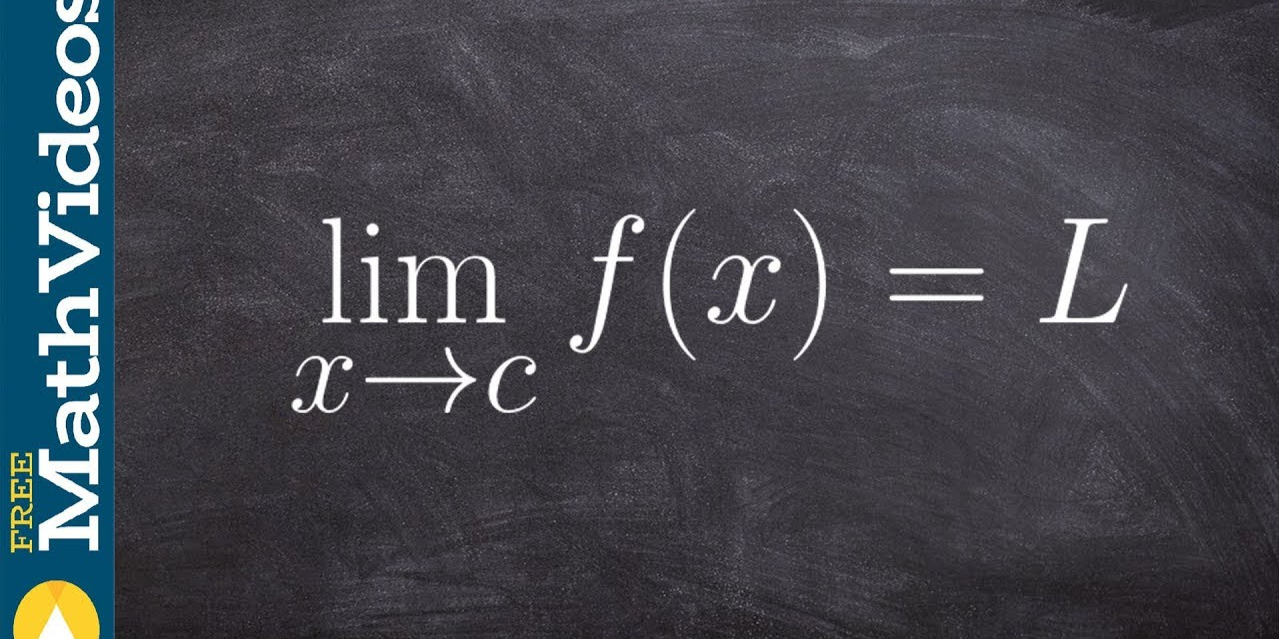¿Qué es el cálculo?

El cálculo es la rama de las matemáticas que investiga las tasas de cambio. Imagina que estás conduciendo tu coche por la autopista. De repente, el semáforo se pone en verde: ¿cómo aumenta tu velocidad en cuanto comienza a moverse hacia su intersección, y cómo se calcula la aceleración? Estos ejemplos ocurren a lo largo de la vida diaria mientras nuestro mundo cambia y se transforma constantemente; en este artículo profundizaremos en su formación. ¿Qué es el cálculo? ¿Qué es la tasa de cambio?

Definición

Definición básica

El cálculo es fundamentalmente sobre entender cómo cambian las cosas y proporciona herramientas para cuantificar cambios, tanto lineales como no lineales. Explora el comportamiento de las funciones mientras cambian con efectos instantáneos así como acumulativos.

Dos ramas principales

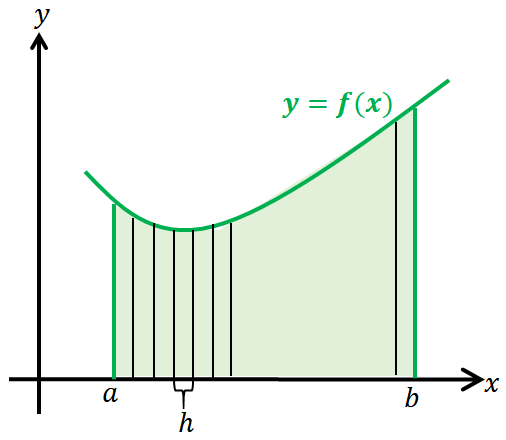
El cálculo se puede dividir en dos ramas principales: cálculo diferencial y cálculo integral. El cálculo diferencial utiliza derivadas—tasas de cambio que representan tasas de cambio—como su punto focal; ayuda a las personas a comprender mejor las pendientes de curvas, problemas de optimización y movimiento, mientras que el cálculo integral trata principalmente con integrales para acumular y analizar el área bajo curvas como un medio para encontrar cantidades totales como áreas, volúmenes, u otras medidas acumulativas. Ambas ramas se entrelazan sin problemas, utilizando límites como el concepto clave para resolver problemas del mundo real, desde cálculos de velocidad hasta encontrar áreas bajo curvas.

Etimología

El cálculo tiene un origen intrigante en la antigüedad; su nombre deriva de la palabra latina para piedra pequeña (cálculo). Las civilizaciones antiguas dependían de pequeñas piedras o guijarros como herramientas de conteo para los cálculos aritméticos tempranos—una forma primitiva temprana de conteo que permitió a los comerciantes, comerciantes y académicos realizar operaciones matemáticas básicas como suma y resta. Con el tiempo, el cálculo se asoció con principios más sofisticados y sistemas de computación matemática. Durante la Edad Media, "cálculo" se hizo sinónimo de cualquier método o sistema para el cálculo formal. Isaac Newton y Gottfried Wilhelm Leibniz fueron los primeros en desarrollar nuestro marco matemático actual durante el siglo XVII; en ese entonces "cálculo" llegó a simbolizar procesos sistemáticos rigurosos utilizados para estudiar tasas de cambio y acumulación, reflejando su importancia histórica y metodológica.

Historia

Aquí, ofreceremos una breve introducción y revisión histórica sobre la invención del cálculo. Si deseas saber más, siéntete libre de leer sobre quién creó el cálculo aquí.

Los Precursores del Cálculo

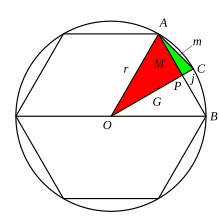
El cálculo no nació de la noche a la mañana, sino que llegó a existir a través de siglos de innovación matemática y pensamiento. Arquímedes, de la antigua fama matemática griega, desarrolló la idea de "indivisibles", un intento temprano de comprender áreas y volúmenes descomponiendo sus mediciones en cantidades infinitamente pequeñas—un precursor temprano de los infinitésimos modernos. Utilizó estas ideas para calcular áreas y volúmenes de círculos y parábolas, así como volúmenes de esferas y cilindros. Liu Hui de la antigua China utilizó el agotamiento—aproximando áreas al inscribir polígonos cada vez más pequeños dentro de ellas para aproximarlas—antes de que el cálculo integral emergiera al resumir todas sus áreas, uniendo así entre cantidades discretas y continuas.

La Creación del Cálculo

Isaac Newton y Gottfried Wilhelm Leibniz inventaron independientemente el cálculo durante finales del siglo XVII, marcando un punto de inflexión histórico en el desarrollo matemático. Newton hizo avances significativos para la ciencia a través de sus estudios de movimiento y fuerzas. Introdujo la derivada para describir los cambios de tasa instantánea—algo integral para entender sus leyes del movimiento y gravitación universal. Leibniz abordó el cálculo desde un punto de vista académico, utilizando notación integral y métodos sistemáticos de cálculo para establecer el cálculo como una disciplina matemática. Su notación para diferenciales impactó enormemente en las representaciones modernas y la enseñanza del cálculo; sus esfuerzos combinados establecieron un marco matemático unificado capaz de resolver problemas en geometría, física y más allá; sin embargo, sus contribuciones dieron lugar a una controversia en curso sobre quién inventó primero el cálculo.

Conceptos Básicos del Cálculo Diferencial

Límites

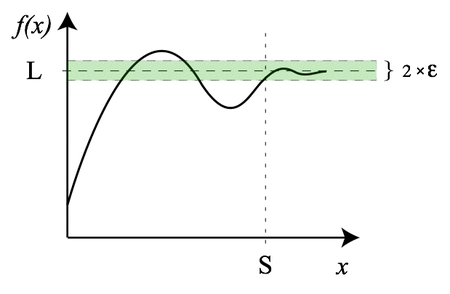
Límites forman el núcleo del cálculo al mostrarnos qué sucede a medida que la entrada se aproxima a un cierto valor, proporcionando información sobre el comportamiento repentino, inesperado o impredecible de las funciones, como alcanzar el infinito o cambios bruscos. A continuación se presentan ejemplos de límites comunes:

- \(\lim_{{x \to \infty}} \frac{1}{x} = 0\)

- \(\lim_{{x \to 0}} \sin(x) = 0\)

- \(\lim_{{x \to 1}} (x^2 - 1) = 0\)

Derivadas

Definición

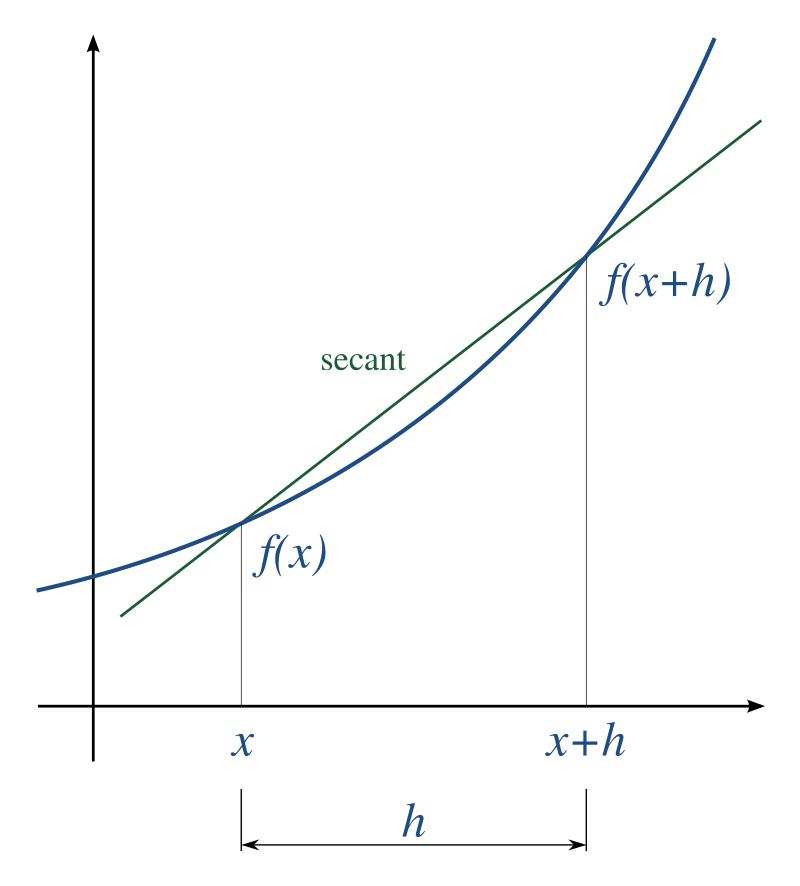
Una derivada, que se denota como \(f'(x)\) o \(\frac{dy}{dx}\), representa la tasa de cambio de una función con respecto a una variable. Las derivadas pueden usarse para determinar la pendiente del gráfico de una función en cualquier punto. Por ejemplo, nos puede ayudar a encontrar los máximos y mínimos locales de las funciones estableciendo f'(x) = 0 y resolviendo para x, lo que se conoce como análisis de puntos críticos. Aquí hay algunas derivadas de funciones comunes:

- Para \(f(x) = x^n\), una función de potencia, la derivada es \(f'(x) = nx^{n-1}\).

- Para \(f(x) = \sin(x)\), una función trigonométrica, la derivada es \(f'(x) = \cos(x)\).

- Para \(f(x) = e^x\), una función exponencial, la derivada es \(f'(x) = e^x\).

Regla de la Cadena

La regla de la cadena es un principio fundamental en cálculo usado para calcular la derivada de una función compuesta. Si \(y = f(u)\) y \(u = g(x)\), entonces la derivada de \(y\) con respecto a \(x\) está dada por \(\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\).

Continuidad y Diferenciabilidad

Continuidad

Una función \(f(x)\) es continua en un punto \(a\) si \(\lim_{{x \to a}} f(x) = f(a)\). La continuidad implica que no hay saltos o rupturas en el gráfico de la función en ese punto.

Por ejemplo, la función \(f(x) = x^2\) es continua en todas partes porque \(\lim_{{x \to a}} x^2 = a^2 = f(a)\). Por otro lado, una función como \(f(x) = \frac{1}{x}\) no es continua en x = 0 porque tiene una asíntota vertical allí, causando una ruptura en el gráfico.

Diferenciabilidad

En cualquier punto a, se puede decir que una función es diferenciable si su derivada puede representarse como una sola línea tangente; la diferenciabilidad requiere que no haya esquinas o cúspides agudas en este lugar y que su tasa de cambio se mantenga consistente a lo largo del tiempo. Un beneficio importante es su continuidad; funciones diferenciables no saltan ni se rompen. Por ejemplo, la función \(f(x) = x^3\) es tanto continua como diferenciable en todas partes donde existe. Sin embargo, no toda función continua puede diferenciarse; por ejemplo, el valor absoluto \(f(x) = |x|\) en esta ubicación debido a esquinas agudas en esa ubicación.

Conceptos Básicos del Cálculo Integral

Integración

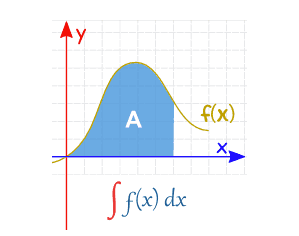
El cálculo integral trata sobre la acumulación y las áreas bajo curvas; sus conceptos clave son la integración, las integrales definidas y las integrales indefinidas. La integración se refiere a encontrar la integral de cualquier función que represente acumulación, ya sea como cantidades acumuladas o áreas bajo curvas. 

Integral Definida

Una integral definida calcula la acumulación de una cantidad sobre un intervalo \([a, b]\). Se denota por \(\int_{a}^{b} f(x) \, dx\). Las integrales definidas tienen muchos usos en diversas áreas, desde el cálculo de áreas bajo curvas y cantidades totales acumuladas hasta la resolución de problemas físicos que involucran masa, carga o distribuciones de probabilidad. A continuación se muestran ejemplos de integrales definidas utilizadas con funciones comunes:

- Para \(f(x) = x\), \(\int_{a}^{b} x \, dx = \frac{b^2}{2} - \frac{a^2}{2}\).

- Para \(f(x) = \sin(x)\), \(\int_{a}^{b} \sin(x) \, dx = -\cos(x) \bigg|_{a}^{b} = \cos(a) - \cos(b)\).

- Para \(f(x) = e^x\), \(\int_{a}^{b} e^x \, dx = e^x \bigg|_{a}^{b} = e^b - e^a\).

Integral Indefinida

Una integral indefinida representa la familia de antiderivadas de una función, denotada por \(\int f(x) \, dx\), donde el resultado es una expresión general que incluye una constante de integración (\(C\)). Las integrales indefinidas tienen un lugar indispensable en muchos contextos matemáticos y prácticos, incluyendo la resolución de ecuaciones diferenciales, encontrar soluciones generalizadas para problemas de acumulación, y modelar procesos de crecimiento/decadencia continuos. Aquí hay algunos ejemplos de integrales indefinidas para funciones comunes:

- Para \(f(x) = x^n\), \(\int x^n \, dx = \frac{x^{n+1}}{n+1} + C\).

- Para \(f(x) = \cos(x)\), \(\int \cos(x) \, dx = \sin(x) + C\).

- Para \(f(x) = e^x\), \(\int e^x \, dx = e^x + C\).

Otros Temas en Cálculo

Aquí principalmente destacamos series, derivadas parciales e integrales múltiples como ejemplos, pero para aquellos que desean profundizar aún más en el aprendizaje del cálculo, ¡recomendamos encarecidamente UpStudy!

Derivadas Parciales

Definición

Las derivadas parciales son derivadas de funciones con múltiples variables, tales como f(x, y, z). Representan la tasa de cambio de la función con respecto a una variable mientras se mantienen constantes las otras variables. Por ejemplo, la derivada parcial de f(x, y) con respecto a x se denota por \(\frac{\partial f}{\partial x}\), y mide cómo cambia f a medida que cambia x, manteniendo y fijo.

Regla de la Cadena

La regla de la cadena en cálculo multivariable se extiende a derivadas parciales. Si \(z = f(x,y)\), entonces \(\frac{\partial z}{\partial t} = \frac{\partial z}{\partial x} \frac{\partial x}{\partial t} + \frac{\partial z}{\partial y} \frac{\partial y}{\partial t}\).

Integrales Múltiples

Las integrales múltiples amplían la integración para incluir funciones con varias variables y variables de múltiples dimensiones, lo que nos permite calcular cantidades en tres dimensiones, como el área de superficie o la masa de láminas. Los integrales triples (\(\int \int \int f(x,y,z) \, dx \, dy \, dz\)) nos permiten calcular volúmenes en el espacio tridimensional, como encontrar volúmenes de regiones sólidas o cargas totales dentro de campos eléctricos, proporcionando un análisis y cálculos precisos de propiedades espaciales.

Series Infinitas

Una serie infinita es una suma de infinitos términos de una secuencia, a menudo escrita como \(\sum_{n=1}^{\infty} a_n\). Además de las series infinitas, existen muchos otros tipos de series, incluidas las series de potencias, que siempre son utilizadas por matemáticos para representar funciones, resolver ecuaciones diferenciales y estudiar la convergencia y divergencia.

Teoremas Comunes del Cálculo

Teorema Fundamental del Cálculo

El Teorema Fundamental del Cálculo crea un vínculo crucial entre la diferenciación y la integración, y consta de dos partes esenciales.

1. La primera parte establece que si \(F\) es una antiderivada de \(f\) en el intervalo \([a, b]\), entonces la integral definida de \(f\) desde \(a\) hasta \(b\) se da por \(\int_{a}^{b} f(x) \, dx = F(b) - F(a)\). Esta parte establece cómo la acumulación de los valores de una función en un intervalo se relaciona con sus antiderivadas.

2. La segunda parte afirma que si \(f\) es continua en \([a, b]\), entonces la función \(F(x) = \int_{a}^{x} f(t) \, dt\) es continua en \([a, b]\), diferenciable en \((a, b)\), y su derivada es \(F'(x) = f(x)\). Esto conecta el proceso de integración con la diferenciación, mostrando que la integración puede ser revertida mediante la diferenciación.

Teorema de Rolle

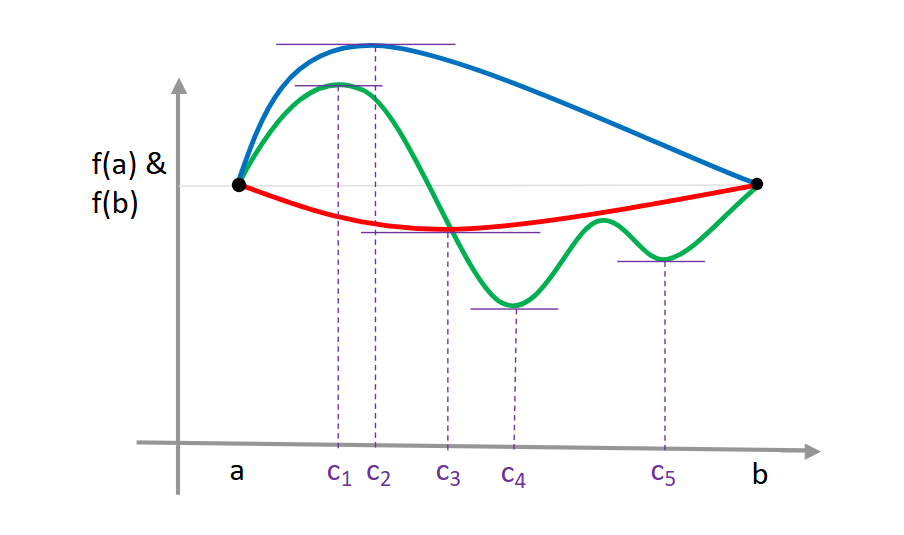
El Teorema de Rolle es un resultado fundamental en cálculo que proporciona condiciones bajo las cuales una función debe tener al menos un punto donde su derivada es cero. Establece que si una función \(f\) es continua en un intervalo cerrado \([a, b]\), diferenciable en el intervalo abierto \((a, b)\), y satisface la condición \(f(a) = f(b)\), entonces existe al menos un punto \(c\) dentro del intervalo abierto \((a, b)\) donde la derivada \(f'(c) = 0\). En otras palabras, hay al menos un punto donde la tangente a la curva es horizontal.

Teorema de Taylor

El Teorema de Taylor proporciona una aproximación de funciones cerca de puntos con polinomios. Si una función f es infinitamente diferenciable en algún punto a, entonces una suma infinita de sus derivadas en este punto, conocida como serie de Taylor, puede expresarse para aproximarla. El teorema se escribe formalmente como \(f(x) = \sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!} (x - a)^n\), donde \(f^{(n)}(a)\) representa la n-ésima derivada de f evaluada en a, y \(n!\) denota el factorial de n.

Aquí hay algunos ejemplos:

1. Función Exponencial (\(e^x\)):

\[e^x = \sum_{n=0}^{\infty} \frac{x^n}{n!} = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \cdots\]

Esta serie converge a \(e^x\) para todo real \(x\).

2. Función Seno (\(\sin(x)\)):

\[\sin(x) = \sum_{n=0}^{\infty} \frac{(-1)^n}{(2n+1)!} x^{2n+1} = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots\]

Esta serie converge a \(\sin(x)\) para todo real \(x\).

3. Logaritmo Natural (\(\ln(1+x)\)):

\[\ln(1+x) = \sum_{n=1}^{\infty} \frac{(-1)^{n+1}} {n} x^n = x - \frac{x^2}{2} + \frac{x^3}{3} - \frac{x^4}{4} + \cdots\]

Esta serie converge para \(-1 < x \le 1\).

Aplicaciones del Cálculo

El Papel del Cálculo en la Física

El cálculo desempeña un papel indispensable en la ciencia física. Permite a los científicos describir y predecir el comportamiento de los sistemas físicos, proporcionando cálculos precisos que miden el movimiento, las fuerzas y la energía; analizan campos electromagnéticos; además de comprender los principios termodinámicos. El cálculo ayuda en muchas aplicaciones diferentes dentro de estas disciplinas, como la trayectoria de proyectiles utilizando ecuaciones diferenciales, el trabajo de fuerzas realizado a través de distancias utilizando integrales, y el análisis de formas de onda en electricidad o magnetismo, entre muchos otros usos.

El Cálculo en Economía

En economía, el cálculo juega un papel esencial en el modelado y optimización de sistemas financieros, identificando tendencias, prediciendo resultados económicos y modelando el análisis del comportamiento del consumidor a través de la maximización de la utilidad o funciones de demanda que permiten una mejor predicción de las reacciones del mercado o cambios de precios. El cálculo diferencial permite a los economistas calcular las relaciones de costes marginales/ingresos marginales, lo que les permite evaluar estas proporciones al producir una unidad más de un producto/servicio; mientras que el cálculo diferencial permite a los economistas determinar las relaciones de costes/ingresos marginales, lo que ayuda a los economistas a analizar el comportamiento del consumidor, las reacciones del mercado y los cambios de precios con más precisión al ayudar a los analistas económicos a predecir estos números con anticipación.

Referencia:

https://www.math.wustl.edu/~freiwald/131calculusf16.html

https://www.dictionary.com/browse/calculus

https://math.hawaii.edu/~lee/calculus/sawyer.html