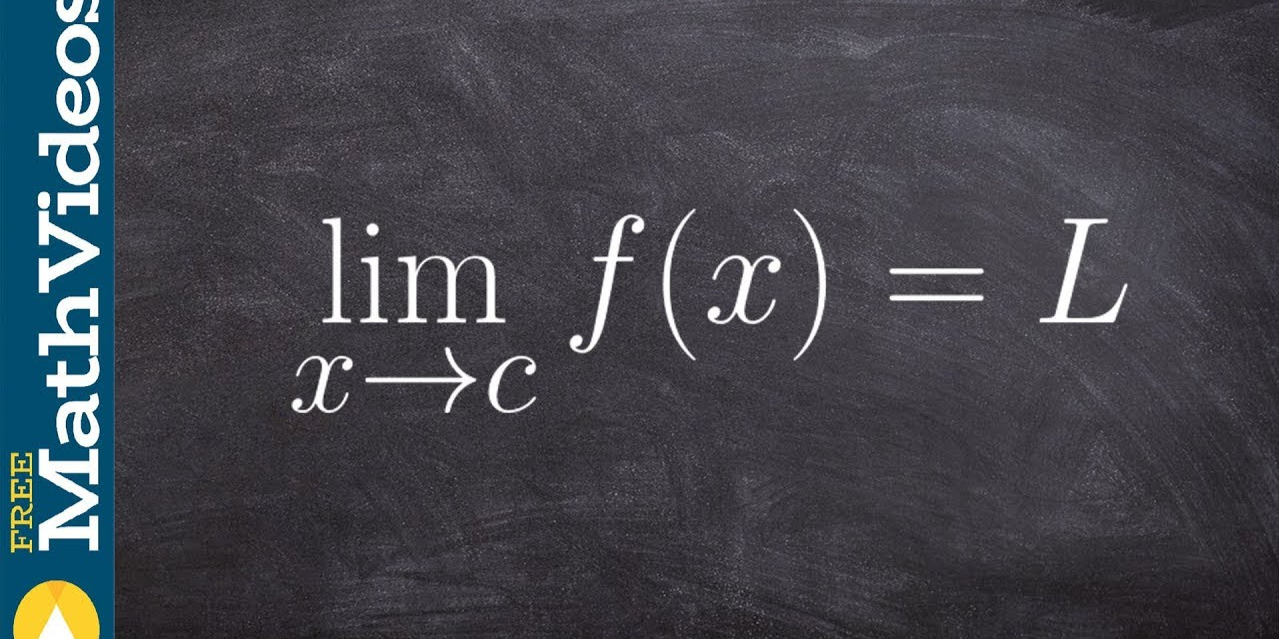¿Qué es Precálculo?

Como es bien sabido, el cálculo es un campo de las matemáticas que se ocupa del estudio de cómo cambian las cosas con el tiempo mediante la diferenciación e integración de funciones, entre otras técnicas. Desafortunadamente, resolver problemas matemáticos usando cálculo puede ser intimidante sin experiencia previa en números complejos y funciones algebraicas, ambos componentes fundamentales. Por lo tanto, el precálculo está diseñado para conectar los aprendizajes previos con el cálculo a través de una serie de cursos matemáticos. Hay dos temas principales en el precálculo: álgebra y trigonometría.

Definición Básica

Definición

Como su nombre indica, el precálculo es un curso que se toma antes del cálculo. Sus cursos dotan a los estudiantes de todo el conocimiento y las habilidades necesarias para abordar problemas de cálculo, basándose en los fundamentos del álgebra y la geometría. Las clases de precálculo pueden servir tanto para los estudiantes de secundaria como una introducción a estudios de cálculo más sofisticados, así como para los primeros años de universidad como una puerta de entrada a estudios de cálculo más especializados.

Dos Temas Principales

El precálculo abarca un conjunto amplio de temas, pero sus enfoques principales son el álgebra y la trigonometría. El álgebra implica aprender símbolos matemáticos y reglas para manipularlos (siendo de particular interés los polinomios, funciones, números complejos y ecuaciones o polinomios); la trigonometría examina las relaciones entre los lados y los ángulos de los triángulos, ¡lo cual es un conocimiento clave cuando se aplica a problemas de cálculo!

Desarrollo del Precálculo

La Creación del Álgebra y la Trigonometría

El álgebra comenzó en la antigua Babilonia, donde los primeros matemáticos utilizaban soluciones simples para ecuaciones lineales y cuadráticas usando técnicas matemáticas primitivas como la división simple. Al-Khwarizmi avanzó este campo durante el siglo IX con enfoques sistemáticos para resolver ecuaciones, así como simbolizando conceptos matemáticos abstractos. La trigonometría se originó durante la Grecia clásica, con Hiparco creando su primera tabla trigonométrica; de aquí surgió la necesidad de la trigonometría para comprender fenómenos astronómicos teniendo en cuenta las propiedades geométricas del triángulo a medida que fue surgiendo debido a la necesidad.

La Invención del Cálculo

El cálculo fue inventado independientemente durante finales del siglo XVII por Sir Isaac Newton y Gottfried Wilhelm Leibniz simultáneamente pero de forma independiente, promoviendo las matemáticas y la ciencia mientras se consolidaba el cálculo como una disciplina esencial—para más detalles, lea nuestro artículo acerca de quién inventó el cálculo!

El Precálculo Es Un Desarrollo Relativamente Nuevo

Hoy en día, el precálculo sirve como un puente indispensable entre los estudios de álgebra y cálculo para los estudiantes, brindándoles una base esencial en conceptos matemáticos clave antes de avanzar a estudios más desafiantes como el cálculo. Gracias a recursos educativos de vanguardia como tecnología interactiva y libros de texto, el precálculo se ha convertido en un componente integral de los currículos modernos de matemáticas.

Temas Algebraicos en Precálculo

Polinomios

Definición:

Los polinomios son expresiones algebraicas compuestas por variables y coeficientes que se suman, restan o multiplican usando exponentes enteros no negativos que representan variables para operaciones de suma, resta o multiplicación. Una expresión polinómica puede contener términos como \(ax^n\), donde \(a\) es un coeficiente y \(n\) es un exponente entero no negativo. La forma general de un polinomio en una variable es \(P(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0\), donde \(n\) es un entero no negativo y \(a_n, a_{n-1}, \ldots, a_1, a_0\) son constantes o coeficientes.

Fórmulas Comunes:

- Polinomio: \(P(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0\)

- Fórmula Cuadrática: \(x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}\)

- Suma y Producto de Raíces: Para \(ax^2 + bx + c = 0\), la suma de las raíces \(= -\frac{b}{a}\) y el producto de las raíces \(= \frac{c}{a}\)

Funciones, Dominio y Rango

Definiciones:

Una función puede definirse como cualquier relación entre entradas y salidas permitidas, donde cada entrada está relacionada directamente con exactamente un valor de salida permitido (valor x o y). El dominio representa todos los valores de entrada posibles, mientras que el rango representa los valores de salida que la función puede producir.

Tipos Principales y Expresiones:

1. Funciones Polinómicas:

Las funciones polinómicas son expresiones que involucran variables y coeficientes, consistiendo en términos de la forma \(ax^n\), donde \(a\) es un coeficiente y \(n\) es un entero no negativo. La forma general es \(P(x) = a_n x^n + a_{n-1} x^{n-1} + \cdots + a_1 x + a_0\). Por ejemplo, \(P(x) = 3x^3 + 2x^2 - x + 5\).

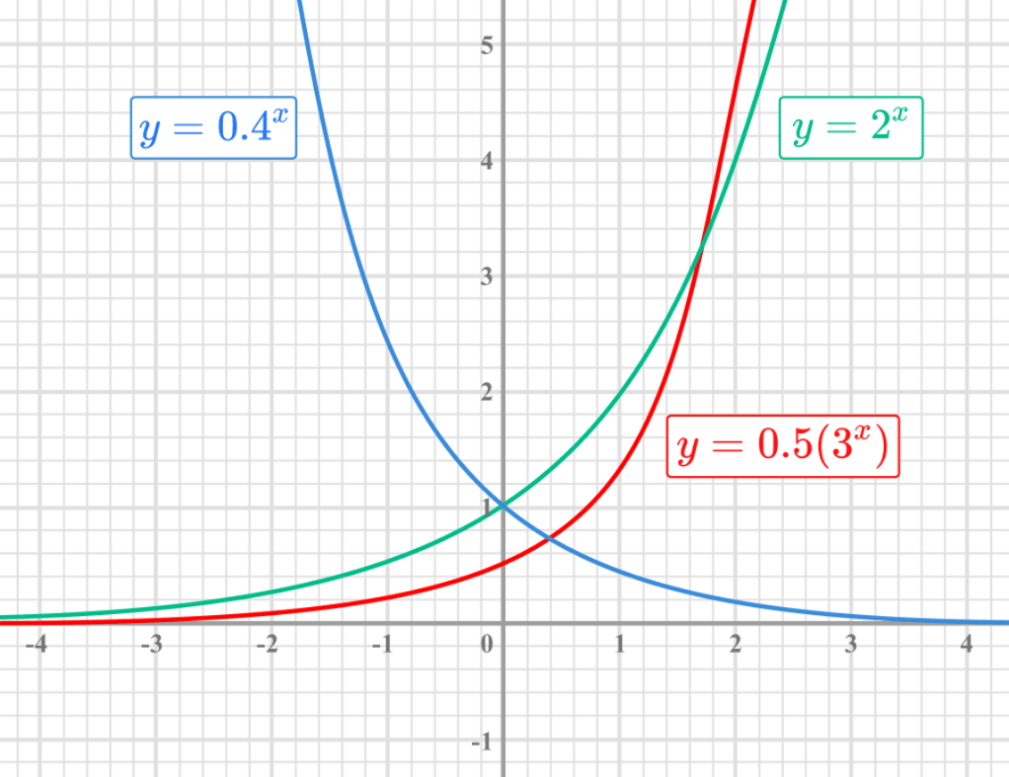
2. Funciones Exponenciales:

Las funciones exponenciales implican la potenciación de una base constante elevada a un exponente variable. La forma general es \(f(x) = a \cdot b^x\), donde \(a\) es una constante, \(b\) es la base, y \(x\) es el exponente. Un ejemplo común es \(f(x) = e^x\), donde \(e\) es la base de los logaritmos naturales, aproximadamente igual a 2.718.

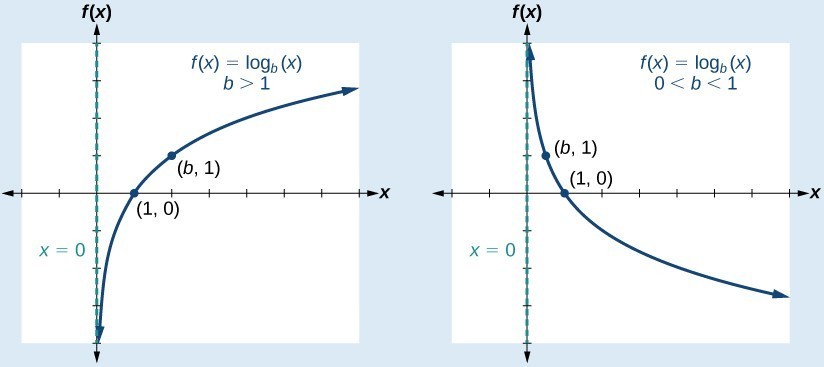
3. Funciones Logarítmicas:

Las funciones logarítmicas son el inverso de las funciones exponenciales y proporcionan el exponente al que se debe elevar la base para obtener un número dado. La forma general es \(f(x) = \log_b(x)\), donde \(b\) es la base y \(x\) es el argumento. Un ejemplo común es el logaritmo natural \(\ln(x) = \log_e(x)\).

Números Complejos

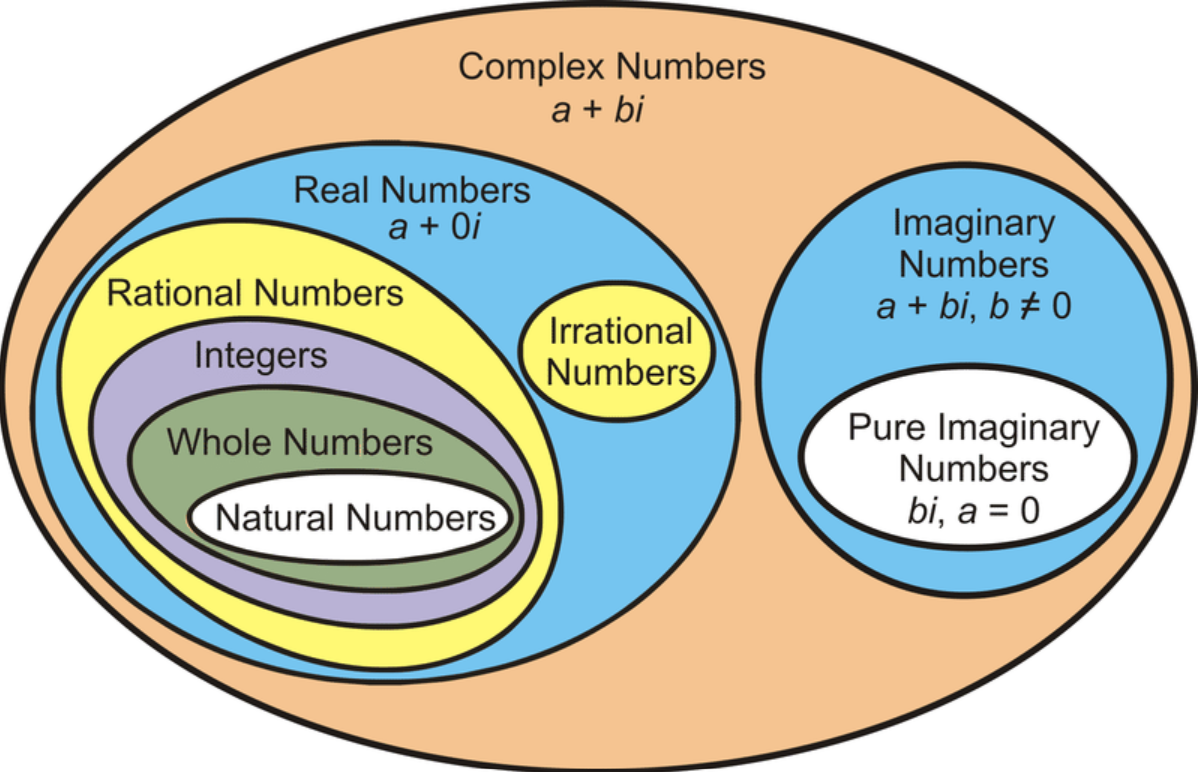
Definición:

Los números complejos extienden el concepto de líneas numéricas unidimensionales al plano complejo bidimensional usando la unidad imaginaria \(i\), donde \(i^2 = -1\). Un número complejo se expresa como \(a + bi\), donde \(a\) y \(b\) son números reales.

Fórmulas Comunes:

- Suma: \((a + bi) + (c + di) = (a + c) + (b + d)i\)

- Multiplicación: \((a + bi)(c + di) = (ac - bd) + (ad + bc)i\)

- Conjugado: El conjugado de \(a + bi\) es \(a - bi\)

- Magnitud: \(|a + bi| = \sqrt{a^2 + b^2}\)

Temas Trigonométricos en Precalculus

Medida de Rotaciones en Grados o Radianes

Una rotación implica girar un objeto alrededor de su centro de rotación mientras el resto se aleja. Este ángulo creado por esta rotación puede expresarse en grados o radianes. Por ejemplo, una rotación de 90 grados gira una figura un cuarto de vuelta alrededor del centro, mientras que una rotación de 180 grados resulta en media vuelta. En radianes, una rotación de círculo completo es \(2\pi\) radianes, equivalente a 360 grados.

Coordenadas Polares y Ecuaciones Paramétricas

Las coordenadas polares son un sistema de coordenadas bidimensional en el cual los puntos se definen como la distancia desde su punto de origen (llamado el origen) y el ángulo desde una dirección de referencia, como el eje x positivo. Cada punto en este sistema de coordenadas puede representarse usando (r, θ), donde r es el radio o distancia al origen desde el origen y "th" representa el ángulo. Cada punto de coordenadas puede entonces representarse usando (r/th).

Las ecuaciones paramétricas describen las coordenadas de los puntos como funciones de un parámetro que varía en un intervalo llamado "t". Por ejemplo, para un círculo con radio r, puede escribirse de la siguiente manera: x(t) = cos(t), mientras que y(t) = sin(t).

Funciones Trigonométricas e Identidades Trigonométricas 

Definición:

Funciones trigonométricas son funciones matemáticas que describen relaciones entre los lados y ángulos de un triángulo rectángulo, como el seno (sin), coseno (cos) y tangente (tan). El seno se relaciona con las razones entre los lados opuestos y las hipotenusas, mientras que el coseno/cos se refiere a los lados adyacentes/hipotenusas, mientras que la tangente es la razón entre adyacente y opuesto.

Funciones y Fórmulas Comunes:

- Seno: \(\sin(\theta) = \frac{{\text{opposite}}}{{\text{hypotenuse}}}\)

- Coseno: \(\cos(\theta) = \frac{{\text{adjacent}}}{{\text{hypotenuse}}}\)

- Tangente: \(\tan(\theta) = \frac{{\text{opposite}}}{{\text{adjacent}}}\)

- Identidad Pitagórica: \(\sin^2(\theta) + \cos^2(\theta) = 1\)

- Identidades de Suma y Diferencia de Ángulos:

\(\sin(A \pm B) = \sin(A)\cos(B) \pm \cos(A)\sin(B)\)

\(\cos(A \pm B) = \cos(A)\cos(B) \mp \sin(A)\sin(B)\)

Otros Temas en Precalculus

Más allá del álgebra y la trigonometría, el pre-cálculo también abarca temas adicionales que son fundamentales para el cálculo. Si quieres aprender más sobre pre-cálculo, ¡no dudes en visitar Upstudy!

Secuencias

Definición:

Una secuencia es una lista ordenada de números que sigue un patrón o regla específica, en la cual cada término representa un número en la secuencia. Las secuencias son herramientas esenciales para estudiar patrones matemáticos, proporcionando la base para temas más avanzados como series y límites; además, desempeñan un papel esencial en numerosos campos, incluyendo matemáticas, informática y finanzas, en términos de pronóstico de tendencias y modelado de comportamientos.

Fórmulas Comunes:

- Secuencia Aritmética: \(a_n = a_1 + (n-1)d\), donde \(d\) es la diferencia común entre términos consecutivos. Por ejemplo, en la secuencia 2, 5, 8, 11, cada término aumenta en 3.

- Secuencia Geométrica: \(a_n = a_1 \cdot r^{(n-1)}\), donde \(r\) es la razón común. Por ejemplo, en la secuencia 3, 6, 12, 24, cada término se multiplica por 2. Estas fórmulas ayudan a identificar y trabajar con patrones regulares en las secuencias.

Series

Definición:

Una serie es la suma de los términos de una secuencia y puede ser finita o infinita, dependiendo de si contiene un número limitado o ilimitado de términos. Las series se utilizan extensamente en cálculo como herramientas para comprender los conceptos de convergencia y divergencia, así como para resumir secuencias y entender fenómenos relacionados como relaciones de convergencia/divergencia.

Fórmulas Comunes:

- Serie Aritmética: \(S_n = \frac{n}{2} (a_1 + a_n)\)

- Serie Geométrica: \(S_n = a_1 \left( \frac{1 - r^n}{1 - r} \right)\) para \(r \neq 1\)

- Serie Geométrica Infinita: \(S = \frac{a_1}{1 - r}\) para \(|r| < 1\)

Límites y Continuidad

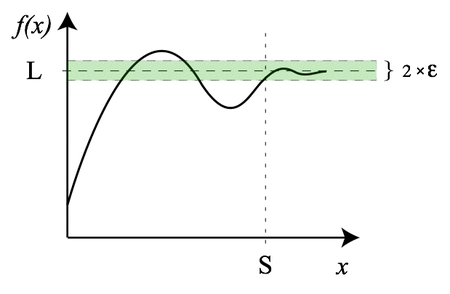
Definición:

El límite se define como el punto al que una función o secuencia alcanza su entrada al acercarse a un cierto valor; la continuidad garantiza que pequeños cambios en una entrada conduzcan a diferencias mínimas en el resultado de esa función.

Fórmulas Comunes:

- Definición de Límite: \(\lim_{{x \to c}} f(x) = L\)

- Condición de Continuidad: Una función \(f(x)\) es continua en \(x = c\) si \(\lim_{{x \to c}} f(x) = f(c)\)

Aplicaciones del Pre-cálculo

Aplicaciones del Pre-cálculo en Finanzas

El pre-cálculo tiene muchas aplicaciones en el ámbito financiero. Por ejemplo, las funciones exponenciales, unas funciones clave en pre-cálculo, pueden ayudar a predecir el interés compuesto y así prever el crecimiento de inversiones; las funciones logarítmicas proporcionan cálculos de amortización de préstamos mientras que comprenden cálculos de valor del dinero en el tiempo; el análisis de secuencias y series puede predecir tendencias del mercado bursátil mientras optimiza carteras de inversión para permitir decisiones informadas por los inversores; los conceptos de pre-cálculo son esenciales en la gestión de riesgos, el análisis de tendencias financieras, y el desarrollo de pronósticos económicos para guiar a las empresas e instituciones financieras por igual.

Aplicaciones del Pre-cálculo en Medicina

El pre-cálculo puede ser utilizado en medicina para modelar procesos biológicos y analizar datos médicos. Las funciones de crecimiento logístico, por ejemplo, pueden modelar el crecimiento poblacional de bacterias o la propagación de enfermedades; las secuencias y series proporcionan información sobre horarios de dosificación de medicamentos así como sus efectos acumulativos. Las funciones trigonométricas juegan un papel integral en la reconstrucción de imágenes del cuerpo humano a partir de técnicas de imagen médica como las resonancias magnéticas (RM) y las tomografías computarizadas (TC); los conceptos de pre-cálculo también son esenciales para modelar la optimización de dosis de medicamentos para la seguridad y eficacia del paciente.

referencia:

https://engineering.usu.edu/students/engineering-math-resource-center/topics/pre-calculus/

https://www.collinsdictionary.com/dictionary/english/precalculus

https://sites.math.washington.edu/~colling/HSMath120/TB201112.pdf