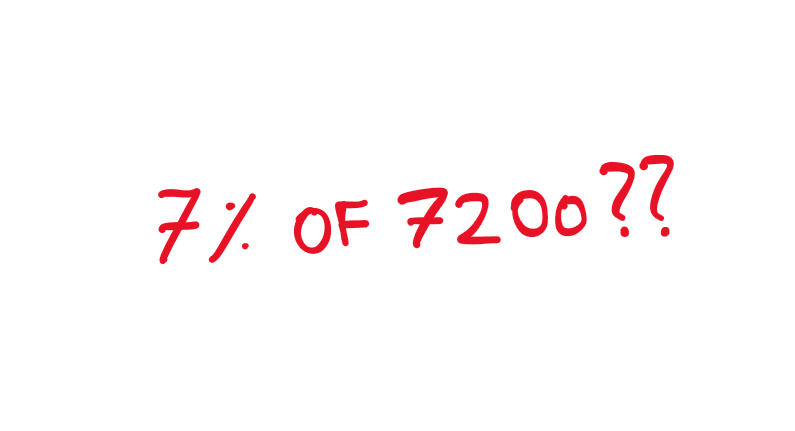Cómo Encontrar un Porcentaje

Entendiendo el Concepto de Porcentajes

Definiendo Porcentajes

Origen y Significado

Porcentaje es un término derivado del latín per centum, o por ciento. Dicho de manera sencilla, los porcentajes representan números o razones sobre 100 que sirven como una forma de comparar valores o proporciones relativas a 100 unidades, con el significado práctico de expresar partes de un todo con una escala universal donde se asume que 100 es su totalidad.

Porcentajes en Contextos Cotidianos

Los porcentajes juegan un papel integral en la vida cotidiana. Por ejemplo, a menudo aparecen al comprar o comer fuera (p. ej. 20% de descuento), las propinas en restaurantes pueden calcularse al 10% o 15% de la cuenta y las instituciones financieras utilizan porcentajes como tasas de interés en préstamos y cuentas de ahorro; la ciencia utiliza porcentajes para cantidades físicas como la humedad o las mediciones de concentración, mientras que los porcentajes desempeñan una función crucial en la interpretación de datos, ayudando a comparar tendencias a través de gráficos y estadísticas.

Qué Representan los Porcentajes

En esencia, los porcentajes representan una proporción que expresa cómo una parte se compara con un todo, multiplicado por 100 para convertirlo en la unidad de porcentaje. En términos matemáticos:

$\text{Porcentaje}=\left(\frac{\text{Parte}}{\text{Todo}}\right)\times 100$

Esta fórmula encapsula todo el concepto de los porcentajes. Por ejemplo, si hay 40 manzanas rojas en una cesta de 100 manzanas, el porcentaje de manzanas rojas sería:

$\text{Porcentaje}=\left(\frac{40}{100}\right)\times 100=40\%$

Visualizando Porcentajes como Partes de un Todo

Las ayudas visuales pueden ser formas poderosas de entender los porcentajes. Un gráfico circular, por ejemplo, divide un círculo en secciones que representan partes proporcionales de su todo; sombrear un cuarto corresponde a 1/4 de un círculo "completo". Los segmentos de barras o cuadrículas ayudan aún más a hacer visible este concepto visualizando cómo las porciones más pequeñas o más grandes se relacionan con el monto total.

Fundamentos Clave de la Fórmula

Entender los porcentajes requiere familiarizarse con su fórmula fundamental:  

$\text{Porcentaje}=\left(\frac{\text{Parte}}{\text{Todo}}\right)\times 100$

A partir de esta fórmula, hay tres tareas comunes: encontrar el porcentaje, determinar la parte (numerador), o identificar el todo (denominador). Estas variaciones son:

1. Para encontrar el porcentaje:

$\text{Porcentaje}=\left(\frac{\text{Parte}}{\text{Todo}}\right)\times 100$

2. Para encontrar la parte:

$\text{Parte}=\frac{\text{Porcentaje}\times \text{Todo}}{100}$

3. Para encontrar el todo:

$\text{Todo}=\frac{\text{Parte}\times 100}{\text{Porcentaje}}$

Variaciones en Escenarios

Estas fórmulas se adaptan a múltiples escenarios. Por ejemplo, si una puntuación de examen es 80 (la parte) de un total de 100 puntos (el todo), el porcentaje de la puntuación es:

$\text{Porcentaje}=\left(\frac{80}{100}\right)\times 100=80\%$

Alternativamente, si sabes que un precio fue reducido en un 20% (porcentaje) y la reducción es de $50 (parte), el precio original puede calcularse como:

$\text{Todo}=\frac{50\times 100}{20}=250$

Métodos Prácticos para Encontrar Porcentajes

Estrategias de Cálculo Mental

Bloques de Construcción

Una poderosa estrategia de cálculo mental implica descomponer los porcentajes en partes más pequeñas y manejables. Referencias comunes como 50%, 10% y 1% simplifican los cálculos:  

1. 50%: Divide el total a la mitad. Por ejemplo, el 50% de 200 es $200÷2=100$.

2. 10%: Divide el total por 10. Por ejemplo, el 10% de 240 es $240÷10=24$.

3. 1%: Divide el total por 100. Por ejemplo, el 1% de 240 es $240÷100=2.4$.

Usando estos bloques de construcción, se pueden calcular porcentajes compuestos. Por ejemplo, para encontrar el 65% de 240:

- 50% de 240 = $240÷2=120$

- 10% de 240 = $240÷10=24$ 

- 5% de 240 =$\left(10\%÷2\right)=12$ 

Súmalos: $120+24+12=156$. Por lo tanto, el 65% de 240 es 156.

Conversión Rápida de Fracciones

Reconocer que los porcentajes a menudo corresponden a fracciones hace que los cálculos sean más rápidos. Por ejemplo:  

- 50% = $\frac{1}{2}$

- 25% = $\frac{1}{4}$

- 20% = $\frac{1}{5}$

- 33.33% = $\frac{1}{3}$

Si necesitas el 33% de 300, reconoce que $\frac{1}{3}$ de 300 es simplemente $300÷3=100$.

Estimación para Decisiones Cotidianas

En situaciones de la vida real, los cálculos precisos a menudo no son necesarios. Por ejemplo, al dejar una propina, puedes estimar el 15% de una cuenta de $47aproximandoel10$4.7) y luego sumando la mitad de ese valor para el 5% ($2.35). El total es aproximadamente $4.7+2.35=7$.

Uso Eficiente de Calculadoras

Técnicas de Conversión Estándar

Las calculadoras facilitan los cálculos de porcentajes. La clave es convertir el porcentaje a un decimal antes de realizar la multiplicación. Por ejemplo:

Para encontrar el 12% de 900:  

$12\%=\frac{12}{100}=0.12$

Entonces, $900\times 0.12=108$.  

De manera similar, si necesitas calcular el 150% de 120, convierte el 150% a forma decimal $1.5$, luego:  

$120\times 1.5=180$

Uso Avanzado de Calculadoras

Las calculadoras avanzadas tienen teclas de porcentaje integradas que eliminan la conversión manual. Por ejemplo, usar un botón "porcentaje" para calcular el 12% de 900 implica ingresar: $900\times 12\%$, que devuelve directamente 108. Esta característica es particularmente útil para operaciones complejas o repetitivas.

Reducir Errores de Entrada con Funciones de Memoria

Muchas calculadoras ofrecen funcionalidades de memoria (e.g., "M+" o "MRC"). Al calcular múltiples problemas de porcentajes, almacenar resultados intermedios puede reducir significativamente los errores de entrada. Por ejemplo, si usas repetidamente el 15% en cálculos, guarda $0.15$ en la memoria de la calculadora para evitar volver a escribirlo.

Dominando los Porcentajes Usando Proporciones

Comprendiendo la Proporcionalidad

Las proporciones ofrecen una perspectiva alternativa para resolver problemas de porcentajes. Una configuración típica es:

$\frac{\text{Parte}}{\text{Total}}=\frac{\text{Porcentaje}}{100}$

Por ejemplo, para encontrar el 25% de 200:  

$\frac{\text{Parte}}{200}=\frac{25}{100}$

Multiplica cruzado para encontrar:  

$\text{Parte}=\frac{25\times 200}{100}=50$

Aplicaciones en Trucos que Ahorran Tiempo

La proporcionalidad a veces permite atajos. Por ejemplo, si calcular el 32% de 50 parece difícil, puedes intercambiar los valores para calcular el 50% de 32, lo cual es más fácil y produce el mismo resultado $(16)$.

Cultivando la Intuición a Través de la Práctica

La precisión en los cálculos de porcentajes mejora con la práctica. Participa en tareas cotidianas como calcular mentalmente descuentos o impuestos de supermercado. Por ejemplo, al estimar un 20% de descuento en un artículo de $45, aproxima $10\%=4.5$ y dóblalo para obtener $9$. Esto aporta rapidez y confianza.

Aplicaciones Avanzadas e Ideas

Cambio y Diferencia Porcentual

Formulando el Cambio

Comprender los cálculos de cambio porcentual es vital en diversos dominios, desde las finanzas y la economía, hasta escenarios de la vida cotidiana. Los cambios porcentuales miden cualquier aumento o disminución relativo entre un valor original y su nuevo valor equivalente.

Las fórmulas son las siguientes:

1. Para un aumento porcentual:

$\text{Aumento Porcentual}=\frac{\text{Nuevo Valor}-\text{Valor Original}}{\text{Valor Original}}\times 100$

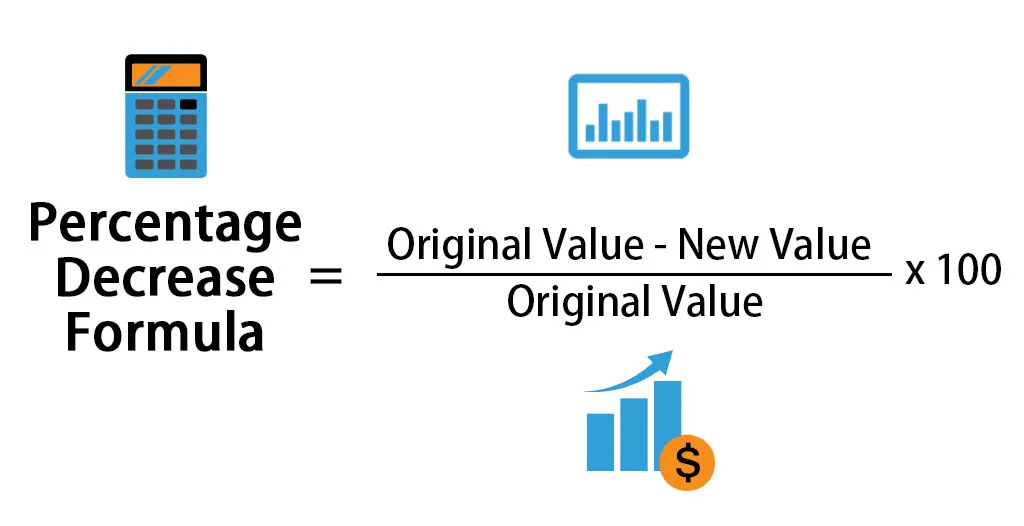
2. Para una disminución porcentual:

$\text{Disminucioˊn Porcentual}=\frac{\text{Valor Original}-\text{Nuevo Valor}}{\text{Valor Original}}\times 100$

Por ejemplo, si el precio original de un artículo es $100yelnuevoprecioaumentaa$120, el aumento porcentual es:

$\text{Aumento Porcentual}=\frac{120-100}{100}\times 100=\frac{20}{100}\times 100=20\%$

De manera similar, si un salario disminuye de $5,000a$4,500, la disminución porcentual es:

$$\text{Disminucioˊn Porcentual}=\frac{5000-4500}{5000}\times 100=\frac{500}{5000}\times 100=10\%$$

Introduciendo Porcentajes Relativos

Si bien los cambios porcentuales absolutos son fáciles de calcular, la diferencia porcentual es útil para comparar dos valores en relación con su promedio. La fórmula para la diferencia porcentual es:

$\text{Diferencia Porcentual}=\frac{|{\text{Valor}}_1-{\text{Valor}}_2|}{\left(\frac{{\text{Valor}}_1+{\text{Valor}}_2}{2}\right)}\times 100$

Por ejemplo, si las puntuaciones de dos equipos son 70 y 80:

$\text{Diferencia Porcentual}=\frac{|80-70|}{\left(\frac{80+70}{2}\right)}\times 100=\frac{10}{75}\times 100=13.33\%$

Decodificando Porcentajes Contextuales

Interpretar los cambios porcentuales requiere comprender el contexto. Un incremento del 20% en una inversión puede representar un crecimiento financiero significativo, mientras que un descuento del 20 por ciento en las compras de comestibles representa más comodidad que ganancia financiera. Al entender su importancia dentro de entornos del mundo real, las ideas basadas en porcentajes se convierten en conocimientos relevantes con significado real.

Visualización de Porcentajes

Representando Porcentajes con Herramientas Visuales

Las ayudas visuales ayudan a transformar porcentajes abstractos en representaciones intuitivas. Las herramientas comunes utilizadas para esto incluyen:

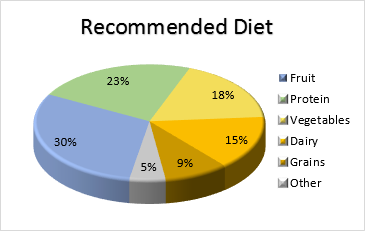
1. Gráficos de Pastel: Los gráficos de pastel hacen sencillo y claro comparar diferentes áreas, como mostrar cómo se ha distribuido tu presupuesto proporcionando una instantánea instantánea de la asignación porcentual de cada categoría.

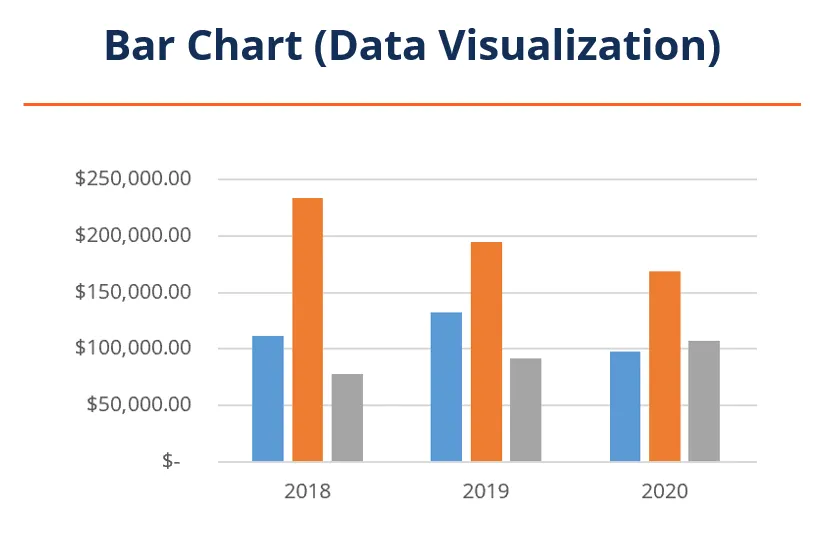
2. Gráficos de Barras: Representan porcentajes junto con datos numéricos, como las tasas de crecimiento de ventas.

3. Mapas de Calor: Se utilizan típicamente cuando se trabaja con grandes conjuntos de datos (por ejemplo, hojas de cálculo). Comunican visualmente porcentajes altos/bajos utilizando indicadores de intensidad de color.

Ejemplo de Gráfico de Pastel y Gráfico de Barras (Fuente). Cada uno proporciona información valiosa. Un gráfico de pastel podría mostrar que el 40% de los gastos diarios se destinan a pagos de alquiler mientras que un gráfico de barras muestra un aumento del 25% en las ventas trimestrales en comparación con el trimestre anterior (fuente).

Aprovechando la Tecnología para la Visualización Instantánea

Las herramientas modernas como Microsoft Excel o Google Sheets simplifican la representación de datos basada en porcentajes. Las hojas de cálculo generan gráficos de barras o gráficos de pastel con solo unos clics una vez que se ingresan los porcentajes. Además, herramientas como Tableau y Power BI ayudan a los profesionales a explorar y analizar grandes conjuntos de datos visualizando porcentajes de manera dinámica.

Más Allá de las Muestras Estáticas—Herramientas Interactivas

Herramientas interactivas como Google Data Studio o Flourish permiten a los usuarios interactuar con visualizaciones porcentuales. Por ejemplo, un departamento de Recursos Humanos podría crear un panel donde los interesados exploren los porcentajes de diversidad de empleados de manera dinámica en lugar de depender de gráficos estáticos.

Evitando Errores Comunes

Malinterpretación del "Todo" o la "Parte"

Un Contexto Claro Importa

Un error común en los cálculos porcentuales radica en identificar incorrectamente el "todo" o la "parte." Por ejemplo, considere la siguiente afirmación: "El 20% de los trabajadores recibió un incentivo." Sin especificar si aplica a toda la fuerza laboral o a un segmento en particular, el análisis puede volverse engañoso.

Desglose de un Ejemplo Práctico

Para resaltar este error, compare estos escenarios:

1. El 20% de 500 trabajadores significa $\frac{20}{100}\times 500=100$ trabajadores recibieron un incentivo.

2. 20% más que 500 trabajadores aumenta la fuerza laboral total a:

$500+\frac{20}{100}\times 500=500+100=600$

Errores en distinguir "de" versus "más que" pueden resultar en resultados drásticamente diferentes.

Verificación de Errores de Cálculo

Puntos de Referencia para Verificar Porcentajes

Una estrategia práctica para prevenir errores es verificar resultados con puntos de referencia. Por ejemplo:

- Verificación del 50%: Asegúrese de que al dividir a la mitad el valor produce el resultado esperado.

- Verificación del 10%: Verifique que los cálculos coincidan con dividir el número por 10.

Por ejemplo, verificar si el 20% de 80 es 16 se puede verificar dividiendo $80÷10=8$, luego duplicando (para el 20%): $8\times 2=16$.

Calibrando Expectativas mediante Verificaciones Dobles

Realizar un cálculo inverso ayuda a validar su resultado. Si el 25% de 200 es 50, recalcular el todo a partir de la parte dada verifica la precisión:

$\text{Todo}=\frac{50\times 100}{25}=200$

La verificación doble puede parecer redundante, pero puede ahorrar tiempo significativo, especialmente en cálculos críticos.

Aplicaciones del Mundo Real y Desarrollo de Habilidades

Escenarios Prácticos Diversos

Alfabetización Financiera

Los porcentajes son fundamentales en las decisiones financieras. Por ejemplo:

1. Tasas de Impuestos: Comprender los porcentajes permite a las personas calcular correctamente los impuestos sobre la renta o las ventas.

2. Tasas de Interés: Los préstamos y ahorros dependen de comprender estas tasas. Si una cuenta de ahorros ofrece un 5% de interés sobre $1,000anualmente,lagananciaesde$50.

3. Presupuestación: Un hogar puede asignar el 30% de los ingresos al alquiler o el 20% al ahorro, haciendo de los porcentajes una parte integral de la planificación.

Métricas Ambientales y Sociales

Los porcentajes también miden el progreso a gran escala, como:

1. Observaciones Ambientales: Si las emisiones de carbono de una ciudad disminuyen un 15% anualmente, significan mejoras en las medidas de sostenibilidad.

2. Tasas de Participación: Medir el porcentaje de votantes que participan (por ejemplo, 62%) o iniciativas de alfabetización implica utilizar porcentajes para cuantificar el desarrollo social.

Herramientas y Recursos para el Dominio

Herramientas Interactivas de Práctica

Las herramientas interactivas proporcionan formas interactivas de dominar los porcentajes. Sitios como Khan Academy y BBC Bitesize ofrecen módulos personalizados específicamente para cálculos de porcentajes; los cuestionarios en línea también presentan estos recursos que simulan cálculos de porcentajes de la vida real para ayudar en la rapidez y precisión de la resolución de problemas.

Ejercicios Prácticos Simulados

Se pueden simular escenarios del mundo real para construir una comprensión contextual. Por ejemplo:

1. Descuentos en Supermercados: Asignar etiquetas simuladas a artículos y calcular el precio de venta después de reducciones del 30% o 50%.

2. Asignación de Presupuesto: Dividir un ingreso hipotético en porcentajes para ahorros, alquiler y gastos discrecionales para internalizar las aplicaciones de porcentajes.

Conclusión

Los porcentajes, como un concepto matemático esencial, juegan un papel crucial en casi todas las áreas de la vida, desde la presupuestación y planificación financiera hasta la interpretación de datos y la medición científica. Calcular porcentajes eficazmente implica comprender la relación entre parte y el todo, expresada a través de fórmulas intuitivas. Las estrategias mentales, calculadoras o ayudas visuales pueden ayudar a resolver problemas de manera eficiente. Los conocimientos avanzados, como comprender los cambios porcentuales, evitar trampas o aplicar porcentajes en escenarios de la vida real, profundizan aún más su relevancia práctica. Adquirir un conocimiento profundo de los porcentajes no solo ayudará en la toma de decisiones diarias, sino que también equipará a las personas con una habilidad vital indispensable. Practicando cálculos regularmente y explorándolos con diversas herramientas interactivas, cualquiera puede volverse competente con los porcentajes.

Referencias:

https://www.tableau.com/learn/whitepapers

https://undullify.com/data-visualization-101-visualize-common-simple-data-points/