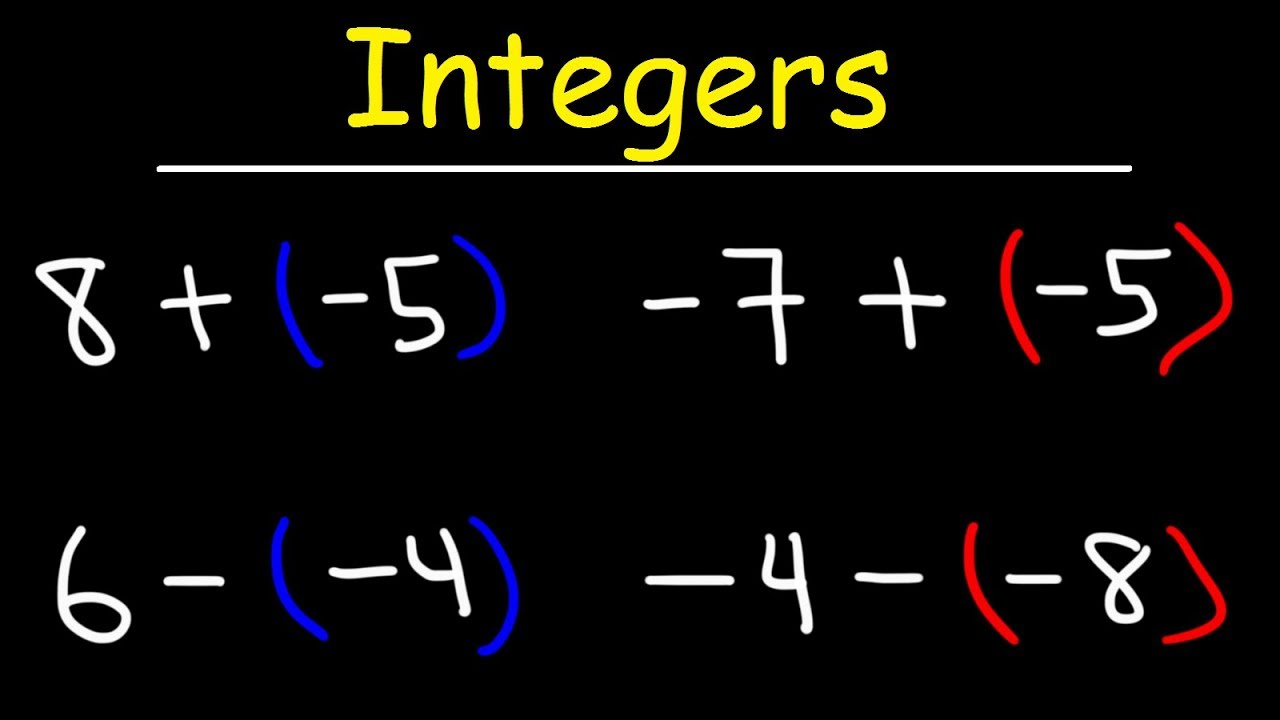¿Qué es un entero?

Definición de Enteros

Entendiendo los Números Enteros

Un entero se define como cualquier número entero que puede ser positivo o negativo e incluye el cero, diferenciándolo así de las fracciones y los decimales. Los números enteros permiten la comparación directa o el cálculo cuando se utilizan en operaciones matemáticas.

Ejemplos de enteros incluyen 1, -3, 4, 0, y -28, y a menudo se utilizan para representar conteos en situaciones del mundo real, como contar manzanas en una cesta, incluso si estos conteos técnicamente podrían ser cero (por ejemplo, al discutir deudas). Cuando nos referimos a enteros, nos referimos a valores que representan conteos en entornos cotidianos, como contar manzanas en una cesta, incluso aunque técnicamente hablando su conteo podría ser cero (por ejemplo, en discusiones sobre deudas).

Por el contrario, números como 0.5 no se consideran enteros porque contienen decimales; de manera similar, valores como 1/3 o 2 no forman valores de números enteros completos, algo esencial en matemáticas para organizar números en diferentes categorías para varias operaciones aritméticas.

La Importancia del Cero en los Enteros

El cero ocupa un lugar único en el conjunto de los enteros. A menudo se considera el entero "neutral", actuando como un límite entre los enteros positivos y negativos. La mayoría de las definiciones de enteros aceptan al cero como un entero válido. Significa la ausencia de cantidad y, en varias operaciones matemáticas, juega un papel significativo.

Por ejemplo, en la suma, añadir cero a cualquier entero no cambia su valor:

a + 0 = a

Donde a es cualquier entero.

En la resta, restar cero de cualquier entero también deja su valor sin cambios:

a - 0 = a

La presencia del cero en el conjunto de enteros permite la inclusión de una gama más amplia de situaciones en la vida real. Por ejemplo, un saldo de cuenta bancaria puede ser cero, indicando ni deuda ni superávit, lo que es una situación representada por el entero 0.

Además, el cero es la identidad aditiva. Si tenemos la ecuación x + 0 = x, muestra claramente que al sumar cero a cualquier entero x se obtiene el entero x mismo. Este concepto es crucial para entender cómo operan los enteros en aritmética.

Tipos de Enteros

Enteros Positivos

Los enteros positivos abarcan los números enteros mayores que cero y son comúnmente conocidos como números naturales o de conteo, ya que los usamos al contar objetos, tales números incluyen 1, 2, 3, 4, 5, etc.

Los enteros positivos forman la piedra angular de las matemáticas y se pueden encontrar en distintos campos, incluyendo finanzas, ingeniería e investigación científica. Cada entero positivo representa una cantidad que se puede sumar o contar; en la aplicación práctica, pueden denotar:

Estudiantes dentro de un entorno educativo (por ejemplo, 25 estudiantes).

Puntos anotados durante un juego (por ejemplo, 30 puntos).

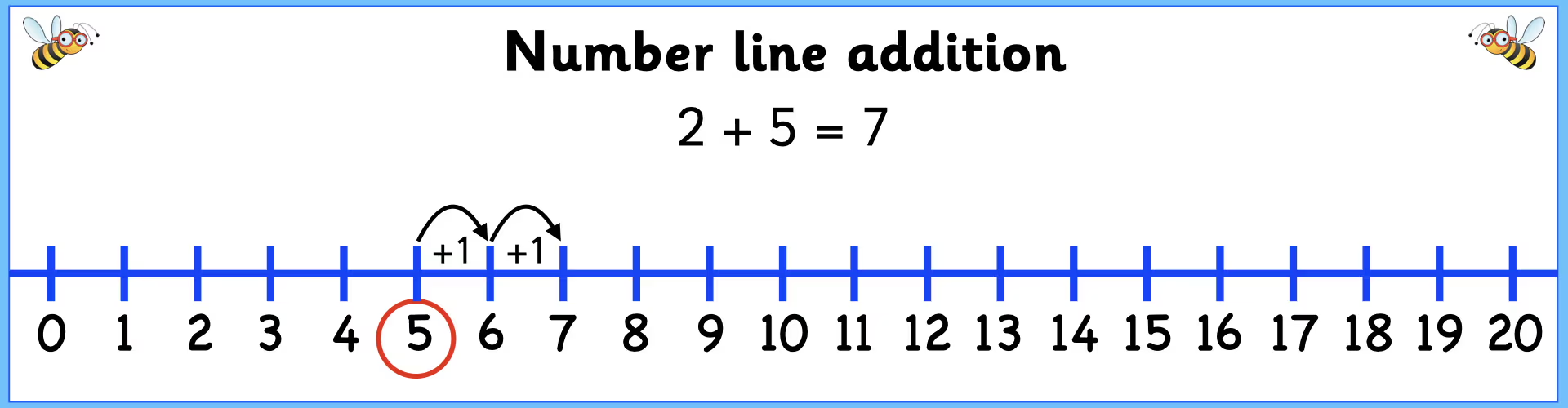
Al trabajar con enteros positivos, realizar operaciones aritméticas sigue las reglas matemáticas básicas. Sumar dos enteros positivos siempre resulta en otro entero positivo:

3 + 4 = 7

De manera similar, multiplicar enteros positivos también resulta en un entero positivo:

$5\times 6=30$

Enteros Negativos

Los enteros negativos son aquellos números enteros que son menores que cero, lo que lleva a la notación de que son lo opuesto de los enteros positivos. Se representan con un signo menos delante de ellos, como -1, -2, -3, y así sucesivamente. Los enteros negativos son cruciales en numerosos escenarios prácticos, especialmente al tratar con deudas o pérdidas.

Por ejemplo, si alguien debe $50, esta deuda se puede representar como -50. Otras áreas donde se aplican los enteros negativos incluyen:

- Temperaturas bajo cero, como -10°C.

- Altitudes por debajo del nivel del mar, como -300 metros.

En las operaciones aritméticas, los enteros negativos demuestran reglas interesantes. Al sumar dos enteros negativos:

-3 + (-5) = -8

El resultado sigue siendo un entero negativo porque los dos "valores negativos" se combinan para formar un valor negativo mayor.

La multiplicación que involucra enteros negativos también sigue ciertas reglas:

$-2\times -3=+6$

En este caso, multiplicar dos enteros negativos resulta en un entero positivo. Por el contrario:

$-4\times 2=-8$

Un entero negativo multiplicado por un entero positivo resulta en un entero negativo.

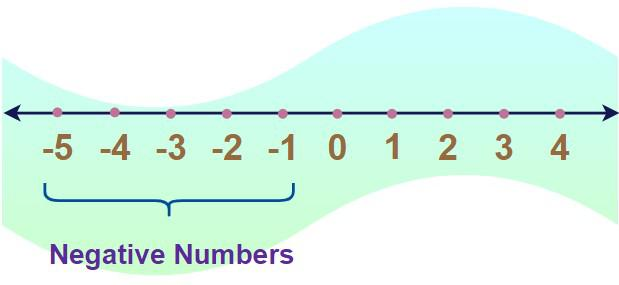
Enteros en una Línea Numérica

Visualizando Enteros

Una forma eficiente de representar enteros que se puede visualizar fácilmente es con una línea numérica. Una línea numérica es una línea horizontal infinita con marcas que representan enteros a lo largo de todo su recorrido en ambas direcciones; el cero actúa como su punto de referencia central y a medida que te mueves hacia la derecha, ves incrementos de uno subir por el lado derecho; moverse hacia la izquierda resulta en números enteros decrecientes (-1, -2, etc.).

Esta herramienta visual es esencial para entender la posición relativa de los enteros. Por ejemplo, en una línea numérica:

- El entero -3 está posicionado a la izquierda de -1, lo que indica que es menor que -1.

- Por el contrario, el entero cuatro está ubicado a la derecha de 2, mostrando que es mayor que 2.

Función del Mayor Entero

La función del mayor entero es un uso fascinante de los enteros en matemáticas y a menudo se denota como [x]. Esta función identifica el mayor entero que es menor o igual a un número dado x. Esencialmente, "redondea hacia abajo" al entero más cercano.

Por ejemplo:

- Para [3.4], devuelve 3, ya que 3 es el mayor entero menor o igual a 3.4.

- En un escenario diferente, [-3.4] resultaría en -4 porque es el mayor entero que todavía es menor o igual a -3.4.

Esta función es especialmente útil en varios escenarios matemáticos, como cálculo o programación informática, donde el comportamiento de redondeo necesita estar claramente definido.

Operaciones con Enteros

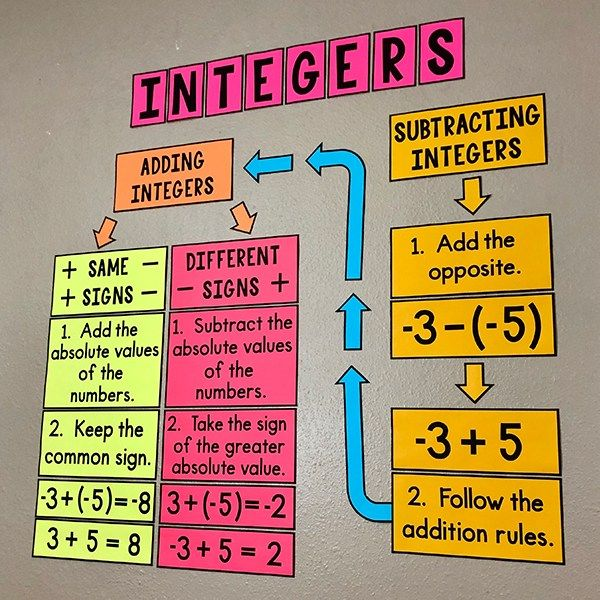
Sumar y Restar Enteros

Al realizar sumas y restas con enteros, los resultados dependen en gran medida de los signos de los enteros involucrados. Sumar dos enteros con el mismo signo da un resultado con el mismo signo. Por ejemplo:

(+3) + (+5) = +8

(-4) + (-6) = -10

Sin embargo, al sumar dos enteros de signos diferentes, debes restar los valores absolutos y tomar el signo del entero con el valor absoluto más alto. Por ejemplo:

(+5) + (-3) se resuelve como 5 - 3 = 2 porque 5 es mayor que 3, y por lo tanto el resultado es positivo.

Por el contrario, (-7) + (+4) se traduce como -7 + 4 = -3 porque 7 es más grande en valor absoluto que 4, lo que lleva a un resultado negativo.

La resta puede simplificarse usando la suma al cambiar el signo del segundo número:

(+3) - (+5) se convierte en (+3) + (-5) = -2

(-6) - (-2) se convierte en (-6) + (+2) = -4

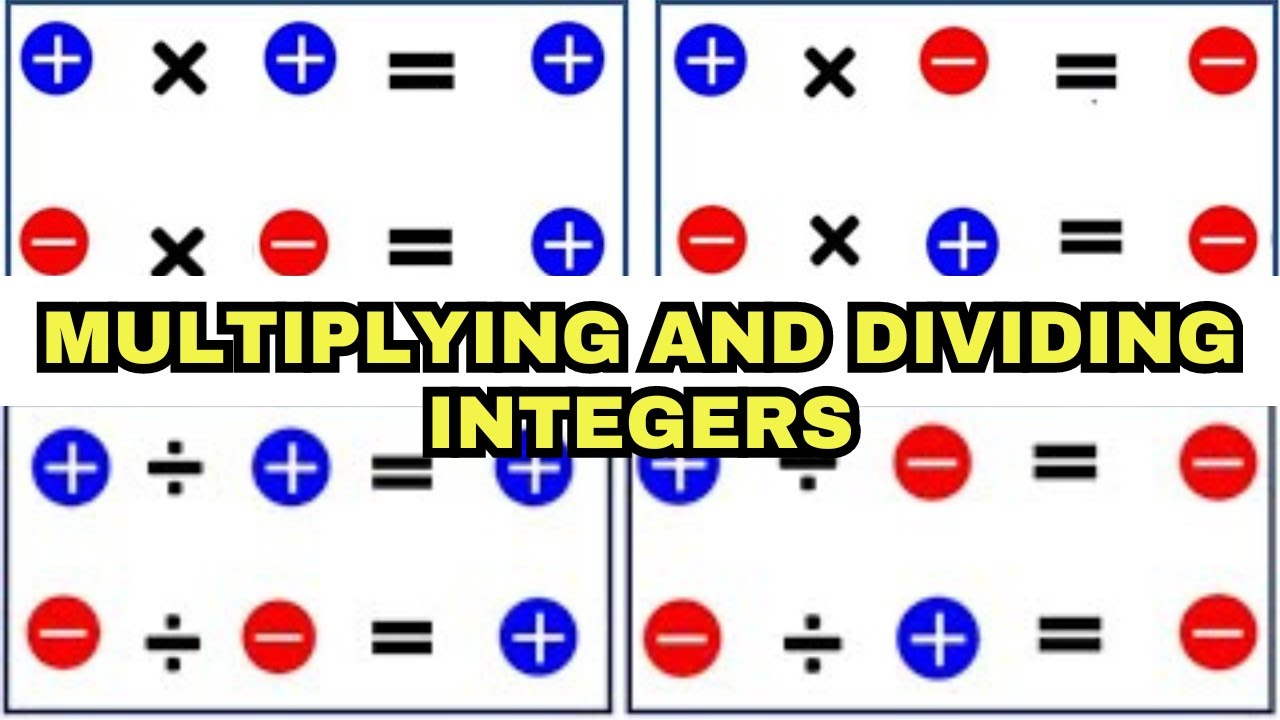
Multiplicar y Dividir Enteros

La multiplicación de enteros suele seguir una regla sencilla también. El producto de dos enteros será positivo si tienen el mismo signo y negativo si sus signos son diferentes. Por ejemplo:

$(+4)\times (+5)=+20$

$(-3)\times (+6)=-18$

Esta regla se mantiene independientemente de cuán grandes o pequeños sean los enteros. Similar a la multiplicación, las reglas para dividir enteros siguen los mismos principios:

(+10) ÷ (+2) = +5

(-12) ÷ (+4) = -3

Al igual que en la multiplicación, dividir dos enteros con el mismo signo da un resultado positivo, mientras que signos diferentes dan un resultado negativo:

(+15) ÷ (-5) = -3

(-16) ÷ (-4) = +4

Estas operaciones forman la base para manejar enteros en cálculos matemáticos, proporcionando una estructura para resolver ecuaciones algebraicas básicas o incluso construcciones matemáticas más complejas.

Propiedades de los Enteros

Propiedad de Clausura

La propiedad de clausura es una característica clave de los enteros en aritmética. Esta propiedad postula que cuando realizas una operación—ya sea suma, multiplicación o incluso resta—sobre dos enteros, el resultado seguirá siendo un entero.

Por ejemplo:

Si tomamos dos enteros, digamos 7 y 3, y los sumamos:

7 + 3 = 10 (que sigue siendo un entero).

- De manera similar, multiplicando enteros:

$4\times 5=20$ (una vez más, un entero).

Sin embargo, es importante notar que si divides dos enteros, el resultado puede no ser siempre un entero. Por ejemplo:

5 ÷ 2 = 2.5,

lo que significa que 2.5 sale del reino de los enteros, demostrando así que la división no necesariamente satisface la propiedad de clausura.

Propiedades Conmutativa y Asociativa

La propiedad conmutativa se refiere al hecho de que el orden en el que sumas o multiplicas enteros no afecta el resultado. Además, esto significa:

a + b = b + a

Y para la multiplicación, esto significa:

$a\times b=b\times a$

Donde a y b pueden ser cualquier entero. Por ejemplo:

3 + 4 = 4 + 3 = 7

$2\times 5=5\times 2=10$

Sin embargo, la conmutatividad no se aplica a la resta o división. Por ejemplo:

$5-3\ne 3-5$,

Ya que los resultados son diferentes.

La propiedad asociativa, por otro lado, expresa que la forma en la que agrupas los enteros no cambia su suma o producto:

- Para la suma: $a+(b+c)=(a+b)+c$

- Para la multiplicación: $a\times (b\times c)=(a\times b)\times c$

Por ejemplo:

2 + (3 + 4) = (2 + 3) + 4 = 9

$2\times (3\times 4)=(2\times 3)\times 4=24$

Conocer estas propiedades ayuda a simplificar ecuaciones complejas y mejorar la eficiencia de los cálculos.

Aplicaciones Únicas de Enteros

Ejemplos de Uso de Enteros en la Vida Real

Los enteros se encuentran en muchos escenarios cotidianos que requieren números claros y sin ambigüedades, particularmente en casos donde no se pueden tener partes fraccionarias. Ejemplos incluyen:

1. Transacciones Financieras:

Si alguien gana $100ygasta$30, puede expresar su ingreso neto como 100 - 30 = 70. Si luego incurre en un gasto de $20, su saldo de la cuenta se convierte en 70 - 20 = 50.

2. Medición de Temperatura:

Los informes meteorológicos a menudo cubren temperaturas usando enteros. Un día frío de invierno podría reportarse como -5 grados Celsius, mientras que un día cálido de verano podría alcanzar +30 grados.

3. Entornos Digitales:

En la programación de computadoras, los enteros se usan frecuentemente para rastrear puntuaciones en juegos, iteraciones en bucles, y banderas en verificaciones de condiciones. Los lenguajes de programación hacen un uso extensivo de enteros como tipo de dato por su simplicidad y eficiencia.

Entender los enteros no solo mejora las habilidades matemáticas, sino que también equipa a las personas con las herramientas necesarias para comprender las representaciones numéricas diarias y cálculos.

El Papel de los Enteros en la Tecnología

A medida que la tecnología se desarrolla, los enteros siguen siendo un componente indispensable de la computación. Su papel se extiende desde la representación de datos en programación, diseño de algoritmos y matemáticas computacionales hasta estructuras de control como bucles e iteraciones. Los programadores utilizan frecuentemente enteros en estructuras de control como bucles por esta razón.

Por ejemplo, al codificar un bucle para iterar a través de una lista de elementos, se utiliza comúnmente el indexado con enteros:

Para $i=0$ (índice inicial),  i < n (total de elementos), incrementando  i proporciona acceso a cada elemento en la lista.

En áreas como inteligencia artificial y ciencia de datos, los enteros se emplean para representar cantidades y categorías discretas. La programación entera, un campo de la investigación operativa, se centra específicamente en problemas de optimización donde algunas o todas las variables están restringidas a ser enteras.

Además, en el desarrollo de juegos, las puntuaciones, niveles y estadísticas de los personajes se manejan frecuentemente usando enteros. El uso de enteros permite a los desarrolladores escribir código más eficiente y confiable, mejorando en última instancia la experiencia general del usuario.

Preguntas Frecuentes

Malentendidos Comunes Sobre los Enteros

Muchos estudiantes y aprendices pueden tener conceptos erróneos respecto a los enteros. Un mito popular que surge del énfasis común en los números naturales en la educación matemática temprana es que todos los enteros deben ser números positivos; en realidad, los enteros incluyen tanto enteros positivos como negativos, así como valores de cero.

Otro malentendido involucra el cero; muchos pueden preguntar si el cero debería contar como un entero en contextos matemáticos, aunque lo más común es que el cero indiscutiblemente pertenezca a este conjunto de enteros.

La Relevancia Futura de los Enteros

A medida que la tecnología digital se expande, también lo hará su dependencia de las operaciones con enteros; los avances en ciencia de datos e inteligencia artificial dependerán aún más de las operaciones con enteros para sus operaciones; las industrias que dependen de algoritmos computacionales dependen cada vez más de las operaciones con enteros: entenderlos ahora preparará a estudiantes y profesionales para futuros desafíos en campos como la informática, la ingeniería y las matemáticas.

En conclusión, los enteros son componentes cruciales en diversos dominios, enfatizando su importancia inherente tanto en la educación matemática como en las aplicaciones del mundo real. Al comprender las definiciones, operaciones y propiedades que rodean a los enteros, las personas crean una base sólida para conceptos matemáticos más avanzados y habilidades prácticas de resolución de problemas que, sin duda, encontrarán a lo largo de sus vidas. Desde el conteo básico hasta los sistemas tecnológicos sofisticados, el papel de los enteros no puede ser exagerado.

Conclusión

En esta exploración exhaustiva de lo que constituye un entero, hemos profundizado en la definición, tipos, aplicaciones, operaciones y propiedades asociadas con estos números esenciales. Los enteros no solo sirven como elementos fundamentales en las matemáticas, sino que también proporcionan marcos para entender diversas situaciones del mundo real. Reconocer su significado en la vida cotidiana—desde la gestión financiera hasta los cálculos científicos—refuerza la necesidad de dominar los enteros. A medida que la tecnología y los métodos de computación evolucionan, mantener un firme entendimiento del papel de los enteros permitirá a las personas navegar el mundo que les rodea con mayor confianza y comprensión. En última instancia, los enteros no son solo conceptos abstractos sino herramientas vitales que facilitan nuestras interacciones diarias y procesos de toma de decisiones.

Referencia:

https://www.qodo.ai/glossary/programming-logic/

https://www.skillsandlearningace.com/blog/how-maths-courses-can-help-with-money-management/

https://www.incharge.org/understanding-debt/types-of-debt/