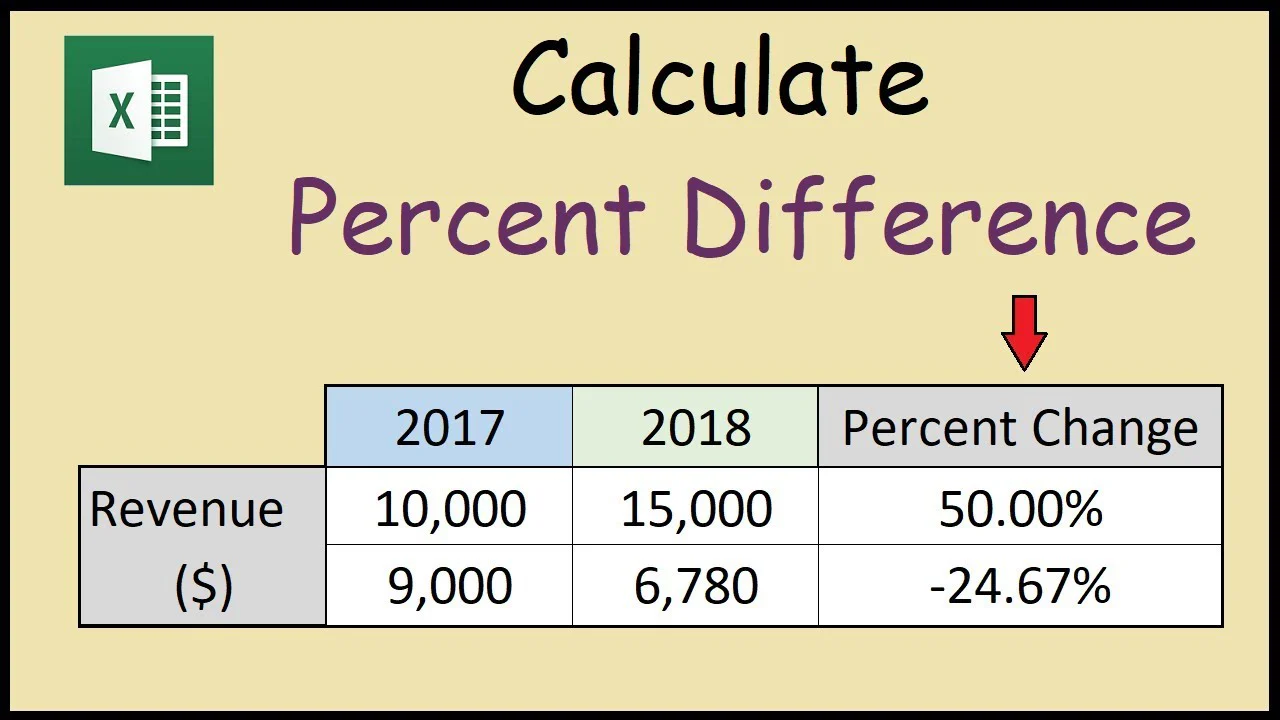
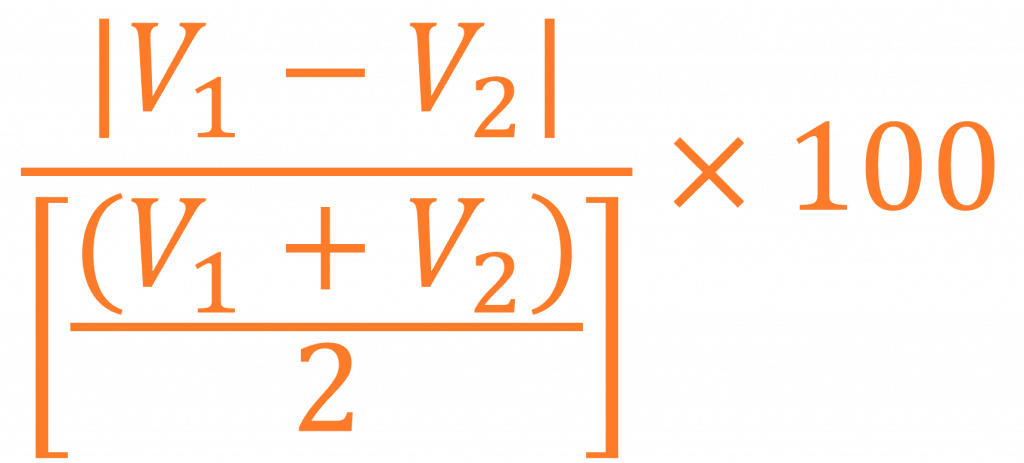¿Cómo Calcular la Diferencia Porcentual?

Fórmula Core y Fundamento Matemático

Definición e Interpretación de Símbolos

La diferencia porcentual cuantifica la disparidad relativa entre dos valores en comparaciones simétricas, donde ningún valor se designa como referencia. No es sinónimo de "cambio porcentual," que mide el crecimiento o la disminución direccional relativa a un valor inicial. La fórmula se expresa como:  

$\text{Diferencia Porcentual}=\left|\frac{V_1-V_2}{\frac{V_1+V_2}{2}}\right|\times 100\%$

Aquí, $V_1$ y $V_2$ representan los dos valores que se comparan. El denominador utiliza el promedio $\frac{V_1+V_2}{2}$ en lugar del valor inicial o final, asegurando simetría.  

Por Qué el Promedio Importa: Detrás de la Fórmula

Usar el promedio como denominador estandariza las comparaciones eliminando el sesgo hacia cualquier valor. Considera dos acciones:  

- Acción A: Aumenta de $50a$100  

- Acción B: Aumenta de $150a$200  

Aunque sus cambios absolutos son idénticos (+50), sus diferencias porcentuales relativas a sus promedios difieren:  

$$\begin{gathered} \text{Accioˊn A: }\left|\frac{100-50}{\frac{100+50}{2}}\right|\times 100\%=66.67\% \\ \text{Accioˊn B: }\left|\frac{200-150}{\frac{200+150}{2}}\right|\times 100\%=28.57\% \end{gathered}$$

Esto demuestra cómo el promedio ancla el cálculo a un punto medio, proporcionando una base normalizada para la comparación.  

Necesidad del Valor Absoluto: Eliminando el Sesgo Direccional

Las fórmulas de valor absoluto están destinadas a asegurar que los resultados permanezcan no negativos, con un énfasis mayor en la magnitud que en la dirección. Cuando se utilizan en entornos de laboratorio, se deben evaluar los errores de calibración entre dispositivos sin favorecer un dispositivo sobre otro. Si la fórmula excluyera el valor absoluto, las diferencias positivas y negativas podrían cancelarse durante los análisis de múltiples mediciones, tergiversando el error total.

Diferencias Estratégicas: Diferencia Porcentual vs. Métricas Similares

Marco Comparativo

- Cambio Porcentual: Calculado como $\frac{V_{\text{final}}-V_{\text{inicial}}}{V_{\text{inicial}}}\times 100\%$, sigue la evolución a lo largo del tiempo.  

- Error Porcentual: Mide la desviación de un estándar: $\left|\frac{\text{Experimental}-\text{Teoˊrico}}{\text{Teoˊrico}}\right|\times 100\%$.  

Punto Ciego Competitivo: Abordando la Confusión de "Manzanas vs. Naranjas"

Antes de aplicar una fórmula, primero valide:

1. Consistencia de Unidades: Convierta todas las medidas a unidades idénticas como kilogramos o mililitros.

2. Alineación Temporal/Espacial: Asegúrese de que las medidas abarquen el tiempo o el espacio geográfico de manera equitativa.

3. Relevancia Contextual: Confirme que las comparaciones cumplan con sus objetivos analíticos.

Ejemplo: Comparar los ingresos anuales $(\$1.2M)$ con los ingresos trimestrales $(\$300K)$ sin ajustar por tiempo da una diferencia porcentual de $\left|\frac{1,200,000-300,000}{750,000}\right|\times 100\%=120\%$, lo cual es engañoso. Anualizar los ingresos trimestrales $(\$300K\times 4=\$1.2M)$ reduce la diferencia porcentual a 0%, reflejando paridad.  

Aplicaciones Científicas Más Allá de los Escenarios de Libros de Texto

Validación de la Replicabilidad Experimental

Porcentaje de diferencia sirve como un umbral de control de calidad en la investigación científica. En un estudio de neurociencia que mide las frecuencias de activación de neuronas (Estudio 1: 15 Hz; Estudio 2: 16.5 Hz):

$\text{Diferencia}=\left|\frac{16.5-15}{15.75}\right|\times 100\%=9.52\%$

Si el umbral de replicabilidad predefinido es 10%, esta diferencia confirma una replicación exitosa.

Normalización de Datos Ambientales

Comparando concentraciones de microplásticos:

- Agua de lluvia ártica: 8 partículas/L

- Agua de lluvia urbana: 32 partículas/L

$\text{Diferencia}=\left|\frac{32-8}{20}\right|\times 100\%=120\%$

Para conjuntos de datos con grandes tamaños de muestra (>1000), aplique transformaciones logarítmicas para mitigar la asimetría:

$\text{Diferencia Ajustada al Log}=\left|\frac{\log (32)-\log (8)}{\frac{\log (32)+\log (8)}{2}}\right|\times 100\%=66.67\%$

Modelado Sociológico: Cuantificación de la Desigualdad

Un coeficiente de brecha de riqueza puede comparar los ingresos de los hogares entre quintiles:

- Promedio del Quintil Superior: 250,000

- Promedio del Quintil Inferior: 35,000

$\text{Diferencia}=\left|\frac{250,000-35,000}{142,500}\right|\times 100\%=118.18\%$

Verificaciones Críticas Pre-Cálculo

Marco de Análisis Dimensional

Utiliza un árbol de decisión para validar la compatibilidad de unidades:

¿Son las unidades idénticas?

- Sí → Proceder

- No → Convertir a unidades comunes (ej., km a metros).

¿Son comparables las escalas de medición?

- Escalas logarítmica vs. lineal requieren normalización.

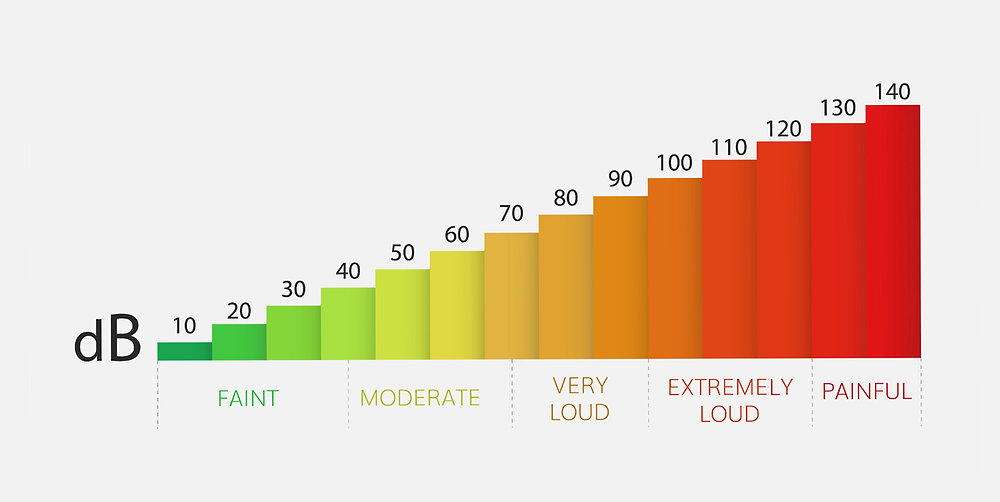
Ejemplo Práctico: Trampa de Escala Decibel vs. Lineal

Comparando intensidades sonoras:

- Mic 1: 50 dB ($10^{-5}$ W/m²)

- Mic 2: 70 dB ($10^{-3}$ W/m²)

Cálculo erróneo usando valores en decibelios:

$\left|\frac{70-50}{60}\right|\times 100\%=33.33\%$

Método correcto usando escalas lineales:

$\left|\frac{0.001-0.00001}{0.000505}\right|\times 100\%=1861.39\%$

Estrategias de Visualización y Narrativa

Mapas de Calor de Umbral Dinámico

Un mapa de calor interactivo puede visualizar rangos aceptables de diferencia porcentual a través de los parámetros:

- Ejes: Ventas mensuales (X) vs. gasto en I&D (Y).

- Gradiente de Color: Verde (0–10% diferencia) a rojo (>50%).

Narrativa de Datos con Granularidad Controlada

Ejemplo para Reportes Corporativos:

1. Resumen Ejecutivo: Diferencia porcentual total en beneficios anuales (15%).

2. Análisis Departamental: Marketing (12%) vs. Producción (22%).

3. Perspectivas Operativas: Fluctuaciones semanales de hasta 35% durante interrupciones en la cadena de suministro.

Protocolo de Manejo de Casos Extremos

Calcular la diferencia porcentual requiere enfoques adaptados en algunos casos extremos para evitar resultados inexactos y engañosos. Tales situaciones podrían involucrar denominadores extremadamente pequeños, tipos de datos mixtos o unidades incomparables, cada escenario debe ser abordado individualmente para producir resultados significativos.

Protocolo de Denominador Casi Cero

Si el promedio de $V_1$ y $V_2$ está cerca de cero, el cálculo de la diferencia porcentual se vuelve inestable. Por ejemplo, comparando 4.95 y 5.05 se obtiene:

$$\begin{gathered} \text{Promedio}=\frac{4.95+5.05}{2}=5.00 \\ \text{Diferencia Porcentual}=\left|\frac{5.05-4.95}{5.00}\right|\times 100\%=2\% \end{gathered}$$

Si el promedio fuera 0.10 en cambio, incluso una pequeña diferencia como 0.05 y $0.15 podría crear una alta diferencia porcentual:

$\text{Diferencia Porcentual}=\left|\frac{0.15-0.05}{0.10}\right|\times 100\%=100\%$

Aquí, informar "los valores se acercan a la paridad" en lugar del porcentaje numérico proporciona una comunicación más clara.

Protocolo de Valores Extremos

Para valores que abarcan múltiples órdenes de magnitud, la diferencia porcentual lineal puede malinterpretar las relaciones. Supongamos que una colonia bacteriana crece de 100 a 10,000 células:

$\text{Diferencia Porcentual}=\left|\frac{10,000-100}{5050}\right|\times 100\%\approx 196\%$

Aunque técnicamente preciso, una comparación en escala logarítmica capta mejor el crecimiento exponencial:

$\text{Diferencia Ajustada al Logaritmo}=\left|\frac{{\log }_{10}(10,000)-{\log }_{10}(100)}{\frac{{\log }_{10}(10,000)+{\log }_{10}(100)}{2}}\right|\times 100\%=66.67\%$

Variaciones Específicas de la Industria en el Cálculo de la Diferencia Percentual

Control de Calidad Farmacéutico

En la fabricación de medicamentos, la diferencia porcentual evalúa la consistencia de los lotes. Por ejemplo, dos lotes de tabletas tienen pesos promedio de 498 mg y 502 mg:

$\text{Diferencia}=\left|\frac{502-498}{500}\right|\times 100\%=0.8\%$

Los límites regulatorios a menudo limitan las diferencias permitidas al 5%, haciendo que este lote cumpla con las normativas.

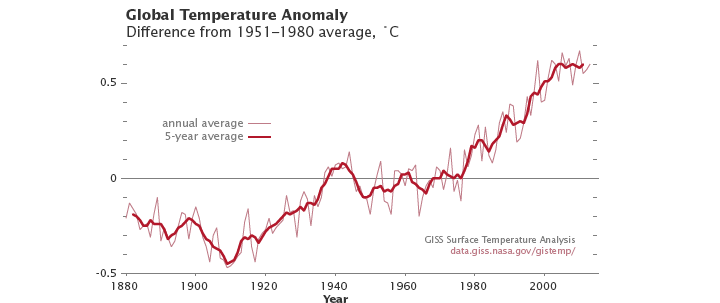
Ciencia Climática: Análisis de Anomalías de Temperatura

La diferencia porcentual ayuda a cuantificar las desviaciones de las temperaturas base. Comparando el promedio global de 2023 (15.2°C) con el promedio del siglo 20 (13.9°C):

$\text{Diferencia}=\left|\frac{15.2-13.9}{14.55}\right|\times 100\%=8.93\%$

Este aumento del 9% provoca evaluaciones de impacto climático.

Consideraciones Computacionales Avanzadas

Implementación Algorítmica para Big Data

Calcular diferencias porcentuales para grandes conjuntos de datos con millones de pares de datos requiere eficiencia computacional. Las operaciones vectorizadas procesan arreglos enteros simultáneamente en lugar de iterar a través de los valores secuencialmente. Considere un conjunto de datos que compara temperaturas diarias de dos sensores durante una década (3,650 pares):

Flujo de Trabajo Vectorizado:

- Almacene lecturas del Sensor A y Sensor B como arreglos $A=[a_1,a_2,...,a_n]$ y $B=[b_1,b_2,...,b_n]$.

- Calcule los promedios: $\text{Avg}=\frac{A+B}{2}$.

- Calcule las diferencias absolutas: $\Delta =|A-B|$.

- Finalice los porcentajes: $\%\text{Diferencia}=\left(\frac{\Delta }{\text{Avg}}\right)\times 100$.

La tecnología de vectorización reduce los tiempos de procesamiento en más del 90% en comparación con los métodos basados ​​en bucles; por ejemplo, 1 millón de pares se pueden procesar ahora en menos de 0.1 segundos en lugar de dos minutos al utilizar bucles tradicionales.

Propagación de Errores en Cálculos de Múltiples Etapas

Cuando los valores de entrada $V_1$ y $V_2$ tienen incertidumbres ($\delta V_1$), $(\delta V_2$), estos errores se propagan a través de la fórmula de la diferencia porcentual. La incertidumbre combinada se calcula mediante derivadas parciales:

$\delta (\text{Diferencia Porcentual})=\sqrt{{\left(\frac{\partial f}{\partial V_1}\cdot \delta V_1\right)}^2+{\left(\frac{\partial f}{\partial V_2}\cdot \delta V_2\right)}^2}$

Derivadas Parciales:

$\frac{\partial f}{\partial V_1}=\frac{200(V_2)}{(V_1+V_2{)}^2},\frac{\partial f}{\partial V_2}=\frac{-200(V_1)}{(V_1+V_2{)}^2}$

Ejemplo: $V_1=100\pm 2$ y $V_2=95\pm 3$ produce:

$\%\text{Diferencia}=5.13\%\pm 1.2\%$

Esto cuantifica la confianza en el resultado, lo cual es esencial para los informes científicos.

Técnicas Pedagógicas para Enseñar la Diferencia Porcentual

Demostraciones Visuales Interactivas

Las herramientas de gráficos dinámicos ayudan a los estudiantes a internalizar el comportamiento de la fórmula. Por ejemplo:  

- Visualización en la Línea Numérica: Grafique $V_1$, $V_2$, y su promedio. A medida que los estudiantes ajustan los valores, la diferencia porcentual se actualiza en tiempo real.  

- Análisis de Sensibilidad: Fije $V_1=50$ y varíe $V_2$ de 30 a 70. Los estudiantes observan cómo la diferencia porcentual alcanza su máximo cuando $V_2$ se acerca a los extremos.

Conceptos Erróneos Comunes y Correcciones

Concepto Erróneo 1: "La diferencia porcentual refleja la disparidad aditiva."

Realidad: Mide la disparidad relativa. Un cambio de 100 a 150 (50% de diferencia) es matemáticamente distinto de 200 a 250 (28.57% de diferencia).

Concepto Erróneo 2: "La fórmula funciona para comparaciones en escala de razones."

Realidad: La diferencia porcentual asume datos en escala de intervalos. Compare diferencias en niveles de pH (escala logarítmica) solo después de convertir a concentración de iones de hidrógeno $[H^{+}]$:

$\%\text{Diferencia en }[H^{+}]=\left|\frac{10^{-{\text{pH}}_1}-10^{-{\text{pH}}_2}}{\frac{10^{-{\text{pH}}_1}+10^{-{\text{pH}}_2}}{2}}\right|\times 100\%$

Evolución Histórica del Concepto de Diferencia Porcentual

Orígenes en la Física Experimental del Siglo XIX

La adopción temprana de la calibración de instrumentos se volvió necesaria debido a estudios de termodinámica y electromagnetismo. Los experimentos de James Clerk Maxwell sobre campos magnéticos a partir de 1873 estandarizaron la presentación de errores con respecto a la diferencia porcentual en la comparación de valores predichos con los observados.

Mejoras Computacionales Modernas

Después de la década de 1950, la computación digital transformó el análisis estadístico:

- Simulaciones de Monte Carlo: Calcular diferencias porcentuales a través de miles de escenarios probabilísticos.

- Modelado Climático: Evaluar la divergencia entre trayectorias de emisiones del IPCC utilizando diferencias porcentuales por celda de cuadrícula.

Implicaciones Éticas en la Presentación de Datos

Manipulación Selectiva de Métricas

Las organizaciones pueden explotar la ambigüedad de las métricas para influir en las percepciones. Por ejemplo:

- Una empresa tecnológica informa de una diferencia del 5% en la eficiencia energética entre dos centros de datos mientras omite que uno es 10 veces más grande.

- Una empresa farmacéutica destaca la diferencia porcentual (simétrica) en lugar del cambio porcentual (direccional) para minimizar el aumento de efectos secundarios.

Transparencia en la Publicación Científica

Revistas como Science ahora exigen:

- Declaración explícita de los umbrales de diferencia porcentual en las secciones de métodos.

- Justificación para elegir la diferencia porcentual sobre otras alternativas (por ejemplo, error porcentual).

Conclusión  

La diferencia porcentual es una herramienta invaluable para cuantificar las disparidades relativas entre muestras similares en comparaciones simétricas, sirviendo como una forma objetiva de cuantificarlas sin emplear métricas sesgadas como el cambio porcentual o medidas basadas en referenciales como el porcentaje de error. Su fundamento matemático—anclado en la fórmula $\left|\frac{V_1-V_2}{(V_1+V_2)/2}\right|\times 100\%$—asegura equidad en el tratamiento de ambos valores, haciéndolo indispensable para escenarios que demandan objetividad, desde pruebas de lotes farmacéuticos hasta detección de anomalías ambientales.

Sin embargo, su eficacia depende de la precisión contextual: utilizar la diferencia porcentual incorrectamente en situaciones que requieren análisis direccional (por ejemplo, tendencias de crecimiento financiero) o evaluaciones de referencia fija (por ejemplo, precisión experimental) corre el riesgo de malinterpretación y tergiversación de los resultados. Los practicantes deben adaptar las metodologías de acuerdo con desafíos únicos, como aplicar transformaciones logarítmicas cuando se estudian estudios de crecimiento biológico o emplear principios de propagación de errores al tener en cuenta las tolerancias de ingeniería, ya que la incertidumbre puede causar interpretaciones erróneas de diferencias de medición y los principios de propagación de errores pueden explicar las incertidumbres de medición cuando se tienen en cuenta las tolerancias de ingeniería con incertidumbres de medición que no pueden medirse fácilmente utilizando metodologías convencionales por sí solas.

Las consideraciones éticas refuerzan su uso responsable. La presentación transparente, como justificar la selección de métricas en estudios revisados por pares o divulgar cálculo de umbrales en informes de sostenibilidad corporativa, es crucial para mitigar riesgos de representación selectiva de datos y crear total transparencia sobre los umbrales de cálculo en informes de sostenibilidad corporativa. Cuando se usa correctamente, la diferencia porcentual puede servir como un lente de claridad, ya sea para evaluaciones de desigualdades socioeconómicas o validación de modelos climáticos. Sobresale como un lente pero solo cuando se combina con una aplicación disciplinada y honestidad narrativa, creando finalmente un diálogo sólido a través de los dominios científicos, industriales y sociales en lugar de mera simplicidad computacional por sí sola.

Referencia:

https://www.mtsu.edu/faculty/wroberts/teaching/log_1.php

https://www.nature.com/articles/s41746-024-01242-1