¿Qué es un rayo en geometría?

Definición de un Rayo en Geometría

Definición Matemática

La geometría define un rayo como una parte de una línea que se extiende infinitamente en una dirección desde un punto final y nunca termina; a diferencia de las líneas que se extienden infinitamente en ambas direcciones o de los segmentos de línea con puntos finales fijos, su longitud no puede determinarse con precisión para esta característica geométrica que proporciona direccionalidad con una extensión infinita en una dirección específica.

Imagina una carretera recta que comienza desde un punto marcado (su punto final), extendiéndose indefinidamente en una dirección; tal carretera podría describirse como un rayo infinito.

Para comprender mejor los rayos, imagínalos como "calles de un solo sentido" de la geometría; cada uno representa un camino que se mueve infinitamente hacia adelante desde donde comenzó. Además, su forma corresponde con el tiempo que avanza mientras el pasado permanece estático y abundan las posibilidades futuras: una analogía que proporciona claridad para entender los rayos.

Notación de Rayo en Geometría

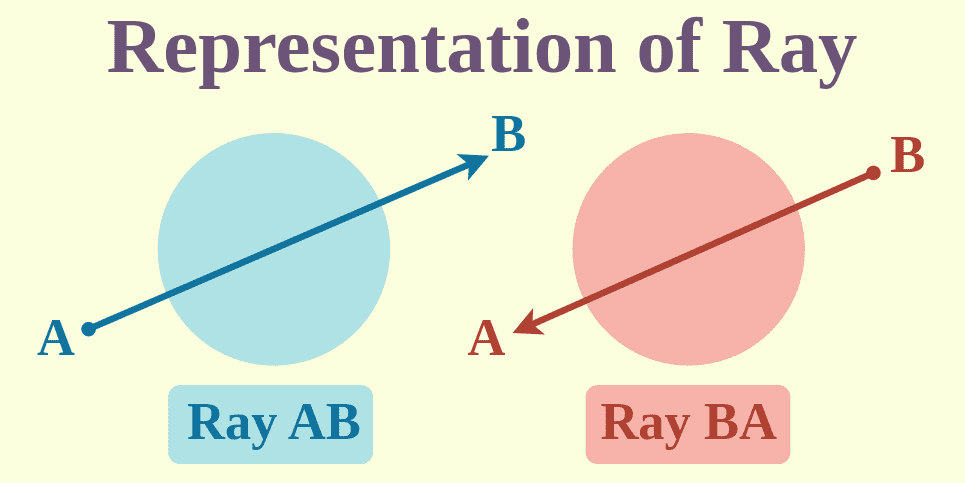
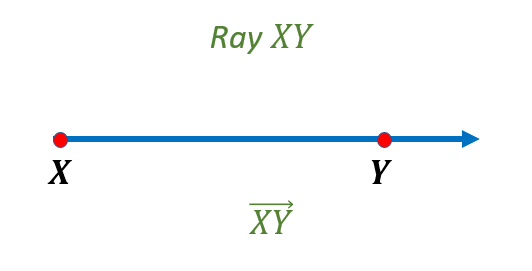
Los rayos se representan usando una notación específica, con el punto final listado primero. Por ejemplo, si un rayo comienza en el punto A y pasa por el punto B en una dirección infinita, se denota como AB →. Nota la flecha apuntando a la derecha, lo que indica la extensión infinita en esa dirección. Es importante destacar que el orden importa—AB → no es lo mismo que BA → porque el punto de inicio (A) siempre debe listarse primero para indicar la direccionalidad del rayo.

Para consolidar este entendimiento, imagina dibujar una línea en papel. Fija el punto A como el origen y dibuja la línea hacia el punto B, agregando una flecha al final. Esta visualización representa el rayo AB →, donde la dirección está claramente de A a B.

Ejemplos Reales de Rayos

Observación Práctica de Rayos

Los rayos no son simplemente conceptos teóricos en geometría; aparecen en todas partes, desde entornos naturales hasta edificios hechos por el hombre a nuestro alrededor, y nos ayudan a comprender mejor su principio central: los rayos nos ayudan a conceptualizarlos de manera intuitiva:

Luz Solar

El sol nos ofrece un ejemplo ideal de un rayo en la vida real. A medida que su punto final permanece fijo, emite rayos de luz continuos que viajan infinitamente hacia afuera en líneas rectas desde su punto central, esta expansión refleja las propiedades infinitas de los rayos geométricos. En días soleados, su interacción con los objetos produce sombras que nos ayudan a visualizar cómo los rayos se extienden en una dirección.

Punteros Láser

Los punteros láser ofrecen una ilustración adecuada de la acción de los rayos. Una vez activados, su rayo láser crea una corriente de luz intensamente enfocada que emana desde un punto (generalmente su fuente emisora de luz) antes de irradiar indefinidamente en todas las direcciones: la ilustración perfecta del viaje enfocado a lo largo de la trayectoria invisible de un rayo.

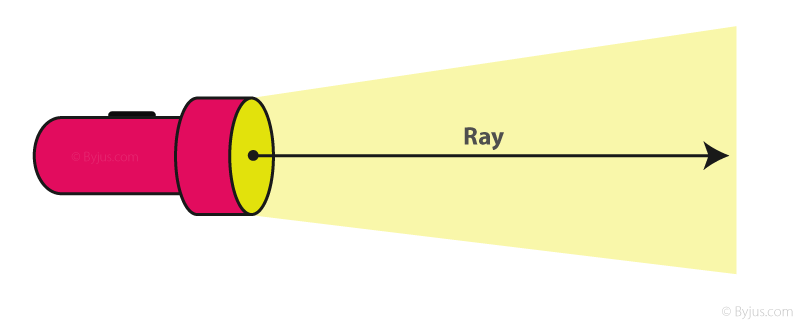
Linternas

Tan pronto como una linterna se activa en una habitación oscura, su haz de luz se expande desde su bombilla de manera ordenada y directa, actuando como una representación exacta de un rayo geométrico que se origina en un único punto y proyecta luz a lo largo de un camino sin interrupciones a lo largo de su trayectoria. Incluso cuando su direccionalidad se disipa a largas distancias.

Aplicaciones en la Vida Cotidiana

Más allá de los ejemplos físicos directos y obvios, los rayos presentan aplicaciones sutiles pero críticas en nuestra vida diaria. Estos ejemplos destacan cómo interactuamos continuamente con estructuras similares a rayos, a menudo sin darnos cuenta:

Navegación Vial

Los dispositivos de navegación modernos, incluidos los sistemas GPS, utilizan trayectorias similares a rayos para ayudarnos a planificar y seguir rutas. Una ruta mostrada por estos sistemas comienza desde tu ubicación actual (que sirve como el punto de inicio fijo), proyectándose hacia tu destino en una dirección específica, similar a cómo se comportan los rayos geométricamente, hasta que finalmente alcanza su punto final, reforzando aún más la importancia de la direccionalidad al recorrer las carreteras al asegurar la alineación entre la representación de extensión infinita.

Vías del Ferrocarril

Un par de vías ferroviarias rectas que se extienden hacia el horizonte evoca la imagen de un rayo. Desde la perspectiva del observador, las vías parecen comenzar desde un punto fijo y extenderse hacia el infinito en una sola dirección, aunque eventualmente pueden curvarse o detenerse.

Haz de un Faro

Los faros proporcionan otro ejemplo sutil pero impactante de rayos en acción. Un haz de faro comienza desde la fuente central de luz y se desplaza hacia el vasto océano, guiando a los marineros en una dirección clara y específica. El haz enfocado se puede ver como una representación de rayos direccionales, ayudando a la navegación de manera similar a cómo los rayos en geometría guían nuestra comprensión de la dirección.

Mangueras de Agua

Imagina el agua saliendo de la boquilla de una manguera como una corriente que se extiende en una dirección definida desde su punto de liberación, disipándose eventualmente pero comenzando como un camino evidente similar a los rayos geométricos con puntos de origen fijos.

Cámaras de Vigilancia

Muchos sistemas de seguridad modernos utilizan haces infrarrojos para la vigilancia. Estos haces se extienden en direcciones específicas desde la fuente de la cámara, creando "rayos" invisibles de detección. Las propiedades de estos haces, caminos rectos que irradian desde un punto final específico, son similares a los rayos en geometría.

A simple vista, los rayos aparecen en todas partes: desde formas tangibles como la luz hasta representaciones más abstractas como los sistemas de navegación. Los rayos como construcciones geométricas fundamentales no solo nos ayudan a comprender mejor los principios matemáticos, sino que también definen y mejoran muchos sistemas que encontramos diariamente en la vida.

Propiedades de los Rayos

Características Fundamentales

Los rayos poseen características distintivas que los diferencian de otros elementos geométricos básicos como las líneas y los segmentos de línea. A continuación, se presentan sus propiedades clave:

Un Solo Extremo

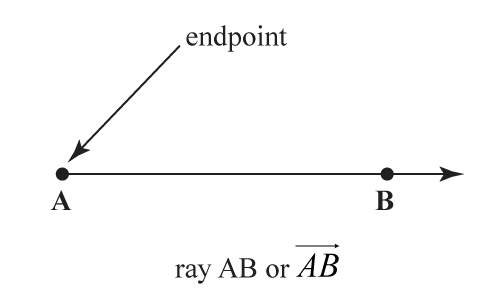
Un rayo siempre comienza en un punto fijo, conocido como el extremo. Este punto de inicio actúa como el origen del rayo y es una característica definitoria que lo diferencia de una línea, que no tiene extremos. Por ejemplo, en el rayo AB →, el punto A es el punto de inicio fijo.

Extensión Infinita

Un rayo infinito se diferencia de su equivalente lineal en que se extiende indefinidamente en una dirección sin límites; una vez que sale de un extremo, continúa sin límites en esa dirección elegida, usualmente representada como una flecha en papel milimetrado.

Longitud Inmedible

Como la longitud de un rayo se extiende indefinidamente en una dirección, su medida no puede ser cuantificada o evaluada con precisión en comparación con los segmentos de línea, que tienen extremos fijos que permiten dichas mediciones.

Naturaleza Direccional

Un rayo tiene una dirección clara y específica determinada por su extremo de inicio y el camino que sigue. Esta característica direccional es crucial para determinar ángulos, graficar desigualdades y otras aplicaciones en geometría. Por ejemplo, la dirección de AB → es de A hacia B, y no puede revertirse o desviarse.

Igualdad de los Rayos

Dos rayos se consideran iguales si y solo si cumplen dos condiciones específicas:

Comparten el mismo extremo.

Se extienden en la misma dirección exacta.

Si estas dos condiciones se cumplen, los rayos son indistinguibles y se consideran iguales. Por ejemplo, los rayos AB → y AC → son diferentes a menos que los puntos B y C se encuentren a lo largo del mismo camino recto originado desde A.

Analogía Ilustrativa:

Imagínate dos corredores que comienzan en una carrera de relevos. Ambos parten desde el mismo bloque de inicio y viajan a lo largo de una pista idéntica - sus caminos son idénticos. Dos rayos también pueden considerarse "gemelos direccionales", compartiendo un origen (extremo) pero apuntando en direcciones opuestas - hacen que sean indistinguibles geométricamente entre sí.

Rayos y Ángulos

Formación de Ángulos por los Rayos

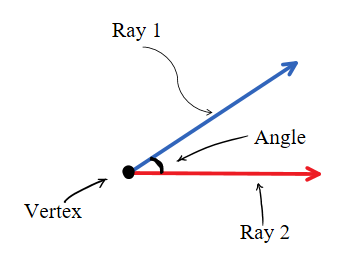
Cuando dos rayos comparten un extremo común, se forma un ángulo. El extremo se convierte en el vértice del ángulo, mientras que los dos rayos que se extienden hacia afuera se llaman los lados del ángulo. Por ejemplo, si dos rayos, OA → y OB →, comparten el extremo O, forman el ángulo ∠AOB.

Los ángulos pueden tomar diversas formas dependiendo de la orientación de los rayos:

Ángulo Agudo: Los rayos forman un ángulo menor a 90°.

Ángulo Recto: Los rayos forman un ángulo perfecto de 90°.

Ángulo Obtuso: Los rayos forman un ángulo mayor a 90° pero menor a 180°.

Rayos en Polígonos

Los lados de un polígono también pueden visualizarse como fragmentos de rayos. Cada lado se origina en un vértice y se extiende hacia el siguiente vértice, asemejándose a segmentos de un rayo que están limitados en longitud.

Un polígono puede verse como "fragmentos de rayos cosidos," donde cada rayo ha sido sincronizado para terminar en un punto específico — formando formas cerradas como triángulos o pentágonos.

Comparando Rayos, Líneas y Segmentos de Línea

Definición de Cada Uno

Para comprender las diferencias entre líneas, segmentos de línea y rayos, es esencial comenzar con sus definiciones precisas:

Línea

Una línea es una forma geométrica interminable sin puntos de inicio o finalización fijos que continúa indefinidamente en ambas direcciones sin llegar nunca a un punto final. La naturaleza infinita de una línea se representa a menudo usando dos flechas en cada extremo para simbolizar su naturaleza infinita.

Segmento de Línea 

A diferencia de una línea, un segmento de línea tiene dos puntos finales fijos y es finito en longitud. Representa una porción específica de una línea con una distancia medible entre los dos puntos finales. Los segmentos de línea se identifican por los dos puntos que los delimitan, por ejemplo, AB, donde A y B son los puntos finales.

Rayo

Un rayo es una combinación de los dos, compartiendo propiedades de ambas líneas y segmentos de línea. Tiene un punto de inicio fijo, conocido como el punto final, y se extiende infinitamente en solo una dirección. Los rayos se denotan con una sola flecha que apunta en la dirección de extensión infinita, como AB →, donde A es el punto de inicio fijo, y el rayo viaja infinitamente hacia B.

Diferenciación Visual

Para diferenciar claramente entre una línea, un segmento de línea y un rayo, la representación visual es invaluable:

Línea

Una línea se representa típicamente por una línea recta con flechas en ambos extremos, denotando su extensión en ambas direcciones. Por ejemplo, AB ↔ demuestra que la línea se extiende infinitamente más allá de A y B.

Segmento de Línea

Un segmento de línea se dibuja con dos puntos fijos, a menudo denominados puntos finales, y no incluye flechas. Su representación, como AB , indica la porción finita de una línea que existe entre los puntos A y B.

Rayo

Un rayo se representa con un solo punto final y una flecha en el otro extremo para significar su dirección de extensión infinita. Por ejemplo, AB → comienza en el punto A (el punto final fijo) y va infinitamente hacia el punto B.

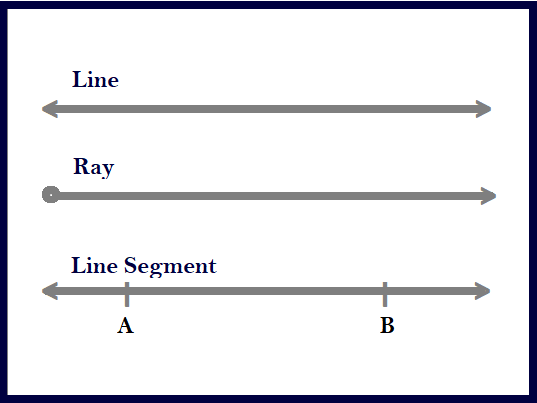
Para comprender mejor estas distinciones, imagina los tres originándose desde el mismo punto:

La línea se extiende infinitamente a la izquierda y a la derecha.

El segmento de línea existe solo entre dos puntos fijos en la línea.

El rayo comienza en un punto y se extiende infinitamente en solo una dirección.

Este tipo de diagrama es una excelente herramienta para comparar visualmente las tres formas geométricas.

Comparación de Aplicaciones Cotidianas

Cada uno de estos elementos geométricos tiene analogías en la vida real, especialmente cuando se compara con diferentes tipos de fuentes de luz:

Líneas

Imagina líneas como caminos de luz interminables que se extienden en ambas direcciones, muy parecidos a un "haz de luz" abstracto sin un punto final o punto de origen, como un haz infinito que ilumina ambos ejes del tiempo del pasado al futuro, extendiéndose infinitamente a través de la eternidad y de regreso al presente. ¡Las líneas del tiempo de hecho se parecen mucho a caminos de luz infinitos!

Segmentos de Línea

El haz tiene un inicio y fin específicos, al igual que un segmento de línea tiene dos puntos finales definidos. La longitud medible del haz corresponde a la porción finita de la línea que representa.

Rayos

Los rayos son análogos a los faros de un coche. Cuando se encienden, la luz se origina en un punto fijo (la bombilla del faro) y se extiende infinitamente en una dirección, iluminando el camino por delante. El haz no se extiende hacia atrás hacia el coche y, por lo tanto, se asemeja perfectamente a la geometría de un rayo.

Una analogía usando fuentes de luz es especialmente útil para entender cómo funcionan las figuras geométricas: las líneas simbolizan la extensión infinita en todas las dimensiones; los segmentos de línea tienen longitud finita y son medibles, mientras que los rayos iluminan solo en una dirección desde su punto de origen, creando así un marco metafórico atractivo para comprender conceptos abstractos más fácilmente.

Rol de los Rayos en la Representación Gráfica de Desigualdades

Rayos en una Línea Numérica

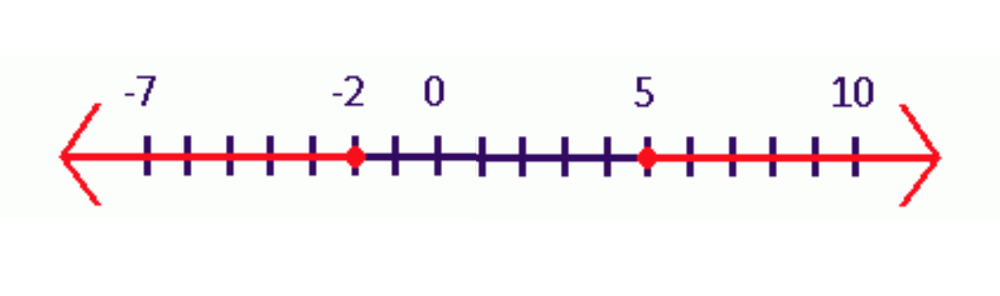
Los rayos desempeñan un papel crucial en la representación visual de desigualdades en una línea numérica. Por ejemplo, la desigualdad x ≥ 7 implica que x incluye todos los valores mayores o iguales a 7, extendiéndose infinitamente en la dirección positiva. En una línea numérica, esta desigualdad se representa comenzando en el punto fijo 7, marcándolo con un círculo lleno (para indicar que se incluye 7), y dibujando un rayo que se extiende hacia la derecha con una flecha para significar extensión infinita.

Ejemplo : Para representar x ≥ 7 :

Dibuja una línea numérica.

Ubica el punto 7 en la línea y márcalo con un círculo lleno.

Dibuja un rayo comenzando en 7, apuntando a la derecha con una flecha para mostrar todos los valores mayores que 7.

De manera similar, para desigualdades como x > 7 , la representación cambia ligeramente. En lugar de un círculo lleno en 7, se usa un círculo abierto para indicar que 7 no está incluido, pero el rayo aún se extiende infinitamente hacia la derecha.

Explorando su Significado

Los rayos en una línea numérica proporcionan una ayuda visual efectiva para comprender desigualdades con crecimiento no acotado o potencial disminuido. Su extensión infinita enfatiza el potencial no acotado o la progresión, lo cual es esencial al entender desigualdades en múltiples contextos.

Aplicación Única: Geometría de Rayos en Gráficos por Computadora

Principios de Trazado de Rayos

El trazado de rayos en gráficos por computadora se basa en un concepto central: el rayo. Los rayos que emanan de fuentes de luz interactúan con objetos virtuales para simular interacciones de la luz; su reflejo, refracción y creación de sombras resultan en imágenes hiperrealistas.

Usos Prácticos en Juegos y Películas

El trazado de rayos se ha convertido en el pilar de los gráficos por computadora modernos, impulsando efectos visuales en películas como Avatar y renderizado fotorrealista en juegos como Cyberpunk 2077. Al simular la iluminación del mundo real a través de rayos, estas industrias crean experiencias visuales inmersivas.

Los rayos en gráficos imitan nuestra comprensión de la luz física pero la extienden infinitamente en dimensiones computacionales, conectando geometría con innovación.

Consejos para Identificar Rayos en Problemas de Geometría

Enfoque Paso a Paso

Observa la figura y busca un único punto extremo conectado a una línea.

Verifica si la línea tiene una punta de flecha en un extremo, indicando extensión infinita.

Asegúrate de que la direccionalidad esté claramente marcada por la flecha para distinguirla de otros elementos geométricos.

Errores Comunes a Evitar

Introducido el "Regla de Confusión de Flechas", los estudiantes a menudo malinterpretan una punta de flecha como un punto extremo en lugar de un indicador de extensión, ¡recuerda que cada rayo solo necesita un punto extremo fijo y mantente firme con este enfoque!

Conclusión

Como uno de los conceptos fundamentales en geometría, los rayos ofrecen conocimientos incomparables sobre los elementos matemáticos. Desde su definición y aplicaciones prácticas, los rayos desempeñan un papel integral en la comprensión de ángulos, polígonos, desigualdades, así como en la navegación de gráficos por computadora, entre muchos otros campos.

Los rayos representan más que líneas estáticas; representan posibilidades infinitas en geometría, innovación tecnológica y vida cotidiana. Comenzando desde un solo punto, podemos imaginar un potencial inagotable de creatividad matemática que quizás nunca agotemos en la vida misma.

Referencia:

https://www.sciencedirect.com/journal/optics-and-lasers-in-engineering

https://developer.nvidia.com/discover/ray-tracing

https://link.springer.com/chapter/10.1007/978-3-540-75388-9_9