Álgebra Lineal Numérica y Álgebra Lineal

¿Estás confundido entre Álgebra Lineal y Álgebra Lineal Numérica como cursos separados? Aunque sus programas de estudio puedan parecer similares, estas materias difieren significativamente en la práctica, como al discutir dinámica de fluidos. El álgebra lineal ofrece caminos de solución teóricos, mientras que el álgebra lineal numérica asegura que estas rutas lleguen a su destino de manera exitosa y segura.

Una Introducción Sencilla al Álgebra Lineal

Definiciones Básicas

El álgebra lineal es la rama de las matemáticas que se ocupa de los espacios vectoriales y las aplicaciones entre estos espacios, incluyendo su intersección. El álgebra lineal estudia líneas, planos y subespacios así como propiedades comunes entre todos ellos.

Vectores y matrices están en el núcleo del estudio del álgebra lineal, actuando como arreglos de números que forman vectores o arreglos bidimensionales en ambas formas; ambas estructuras representan varios objetos matemáticos o transformaciones.

Los espacios vectoriales pueden definirse como colecciones de vectores que pueden sumarse y multiplicarse usando valores escalares para producir vectores adicionales en ese mismo espacio. Forman el concepto central detrás de muchas áreas de las matemáticas y sus aplicaciones.

Las transformaciones lineales son funciones que transfieren vectores entre vectores respetando operaciones como la suma y multiplicación de vectores, representadas como matrices en álgebra lineal. El estudio de estas transformaciones constituye, por lo tanto, uno de sus temas centrales.

Si te interesa esto y deseas saber más, explora el Asesoramiento de Tutores de UpStudy!

Conceptos Clave

Variables (ej., x, y, z)

El álgebra lineal utiliza variables como elementos de espacios vectoriales o coordenadas de cualquier espacio dado; por ejemplo, x, y, y z representan coordenadas en el espacio tridimensional, respectivamente y estas pueden modificarse usando reglas de suma o multiplicación de vectores.

Operadores (suma, resta, multiplicación, división)

El álgebra lineal ofrece varios operadores que funcionan como operaciones matemáticas: suma, resta, multiplicación y división. La suma y resta combinan vectores, mientras que la multiplicación incluye tanto la multiplicación escalar (es decir, multiplicar un vector por un valor escalar) como la multiplicación de matrices, que utiliza la representación matricial de las transformaciones lineales para fines computacionales.

Diferencia entre expresiones y ecuaciones

"Expresión" en álgebra lineal se refiere a cualquier combinación de variables y constantes usando operadores de suma, resta, multiplicación y división. Una ecuación establece que dos expresiones son iguales, y resolver ecuaciones lineales es una de las principales tareas en álgebra lineal, que a menudo incluye encontrar valores de variables que satisfacen conjuntos dados de ecuaciones.

Problemas Estudiados

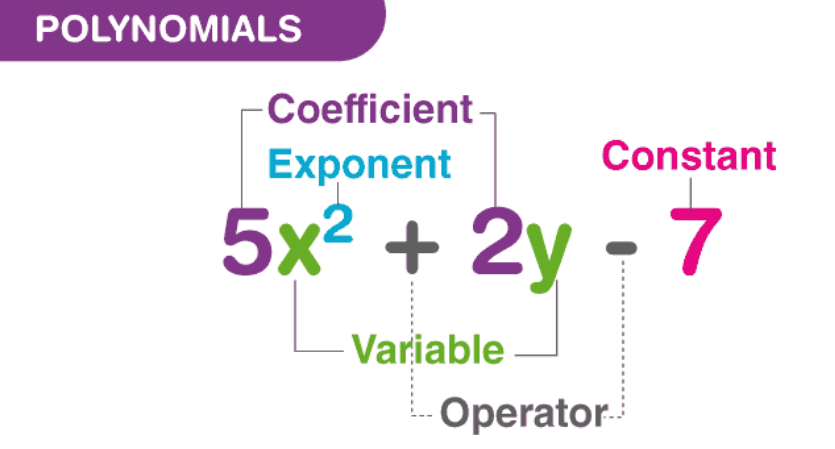
Polinomios

Las ecuaciones características del álgebra lineal usan polinomios como herramientas para localizar los valores propios de la matriz; sus raíces proporcionan una visión clave sobre sus características, tales como sus valores propios o cómo puede comportarse su transformación lineal.

Puedes encontrar muchas preguntas sobre todo lo anterior en el banco de preguntas de UpStudy.

Resolución de sistemas de ecuaciones

Uno de los problemas centrales en álgebra lineal es resolver sistemas de ecuaciones lineales, o encontrar valores que satisfagan múltiples ecuaciones lineales simultáneamente. La eliminación gaussiana, la inversión de matrices y el uso de determinantes pueden proporcionar medios efectivos para lograrlo con éxito.

Matrices y determinantes

Las matrices se utilizan para representar transformaciones lineales y sistemas de ecuaciones lineales. Los determinantes, o los valores derivados al calcular a partir de matrices cuadradas, proporcionan información importante como la invertibilidad. Las matrices y sus determinantes forman la base para comprender las estructuras y soluciones de los sistemas lineales.

Para resolver este tipo de preguntas, puedes probar nuestro Calculadora de Álgebra.

Desarrollo Histórico

Orígenes

El álgebra lineal encuentra sus fundamentos en los estudios de determinantes utilizados durante el siglo XVII para resolver sistemas de ecuaciones lineales, iniciados por matemáticos como Leibniz y Cramer, quienes sentaron las bases para el desarrollo del álgebra lineal.

Crecimiento y Expansión

Matemáticos como Gauss, Jordan y Hamilton contribuyeron significativamente al desarrollo de la teoría de matrices y espacios vectoriales durante los siglos XIX y principios del XX. El álgebra lineal fue entonces formalizada como su propia disciplina matemática gracias a las contribuciones de numerosos matemáticos, resultando en su forma actual.

Contenido Principal de Investigación

Direcciones de Investigación

La investigación actual en álgebra lineal involucra investigar espacios vectoriales más complejos, como los espacios infinitamente dimensionales, y desarrollar métodos innovadores para resolver sistemas lineales. Los investigadores también exploran sus aplicaciones en disciplinas como la física, la informática y la ingeniería.

Teoremas Importantes

Los teoremas clave del álgebra lineal incluyen el Teorema de Rango-Nulidad y el Teorema Espectral, ambos sirviendo como piezas fundamentales para entender y aplicar el álgebra lineal. Estas declaraciones sirven como bloques esenciales en la construcción de tu base de conocimiento en álgebra lineal.

Una Introducción Simple al Álgebra Lineal Numérica

Definiciones Básicas

El álgebra lineal numérica (ALN) es un área del álgebra lineal que se ocupa de desarrollar y analizar algoritmos para realizar cálculos en modelos algebraicos lineales usando computadoras, así como aspectos prácticos asociados con la resolución de problemas similares utilizando computadoras.

Conceptos clave en álgebra lineal numérica incluyen la estabilidad numérica, es decir, cómo se propagan los errores en los cálculos, y la eficiencia, o los recursos computacionales requeridos. Los métodos numéricos deben diseñarse para minimizar los errores mientras se maximiza la eficiencia.

Los problemas de álgebra lineal numérica generalmente requieren cálculos complejos que no pueden completarse manualmente, incluyendo la solución de grandes sistemas de ecuaciones lineales, el cálculo de valores y vectores propios, y la realización de factorizaciones de matrices.

Desarrollo Histórico

Orígenes

El álgebra lineal numérica surgió a mediados del siglo XX debido a la necesidad de resolver grandes problemas científicos e ingenieriles utilizando computadoras, impulsando su formación por la evolución de las primeras computadoras, el surgimiento de la tecnología de cómputo digital y las tendencias relacionadas. Todas estas innovaciones desempeñaron su papel.

Crecimiento y Expansión

Los desarrollos tecnológicos han ampliado enormemente el álgebra lineal numérica como área. Los investigadores han creado algoritmos sofisticados y bibliotecas de software, como LAPACK y MATLAB, que son ampliamente utilizados para aplicaciones de cómputo científico. Además, la computación de alto rendimiento impulsa los desarrollos continuos dentro de la investigación de álgebra lineal numérica.

Contenido Principal de Investigación

Direcciones de Investigación

La investigación en álgebra lineal numérica se centra en desarrollar algoritmos más eficientes y robustos. Esto incluye mejorar los métodos existentes, como los solucionadores iterativos y precondicionadores, así como crear técnicas innovadoras para la computación paralela y distribuida.

Métodos Importantes

El álgebra lineal numérica ofrece muchas herramientas y enfoques útiles, desde solucionadores directos como la descomposición LU y la factorización QR hasta métodos iterativos como la solución de Gradiente Conjugado. Estos enfoques son esenciales al resolver problemas a gran escala para diversas aplicaciones científicas o ingenieriles.

La Conexión Entre el Álgebra Lineal Numérica y el Álgebra Lineal

Sus Principios Fundamentales

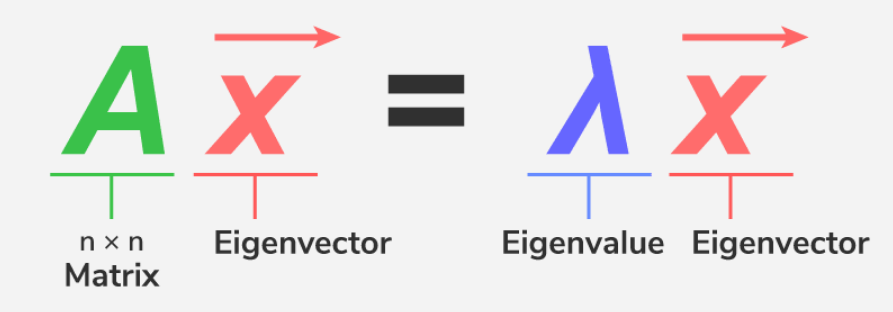
El álgebra lineal y el álgebra lineal numérica comparten principios fundamentales, incluyendo el estudio de espacios vectoriales, transformaciones lineales y propiedades de matrices. Ambos campos dependen de fundamentos teóricos similares que incluyen conceptos como valores y vectores propios, y factorizaciones de matrices.

El álgebra lineal enfatiza aspectos abstractos y teóricos, mientras que el álgebra lineal numérica involucra su implementación práctica en tiempo real a través de algoritmos computacionales para realizar cálculos de álgebra lineal de manera eficiente y precisa.

Los Problemas que Buscan Solucionar

El álgebra lineal busca resolver problemas teóricos mediante la comprensión de espacios vectoriales y transformaciones lineales, así como sus propiedades, demostrando teoremas sobre las estructuras de estos espacios y encontrando soluciones generales a sistemas de ecuaciones lineales.

El álgebra lineal numérica se especializa en resolver problemas prácticos que surgen de aplicaciones científicas e ingenieriles, incluyendo la creación de algoritmos para resolver grandes sistemas de ecuaciones lineales de manera eficiente y precisa, mientras se calculan valores y vectores propios eficientemente y se realizan factorizaciones de matrices precisa y rápidamente.

La Diferencia Entre el Álgebra Lineal Numérica y el Álgebra Lineal

Áreas de Enfoque

Investigación Teórica Abstracta

El álgebra lineal se centra en gran medida en la investigación teórica que implica investigar propiedades de espacios vectoriales y transformaciones lineales, así como desarrollar un conocimiento profundo de las estructuras matemáticas involucradas. La investigación en álgebra lineal a menudo surge de un interés por entender principios matemáticos fundamentales y crear teorías novedosas.

Aplicaciones Computacionales

El álgebra lineal numérica enfatiza las aplicaciones computacionales de los cálculos de álgebra lineal en computadoras. Esto implica desarrollar algoritmos y software para realizar cálculos de álgebra lineal, como resolver grandes sistemas de ecuaciones lineales y calcular valores y vectores propios y factorizaciones de factores de matrices, todo con el objetivo de desarrollar soluciones precisas a problemas prácticos de ingeniería científica.

Relación de Subordinación

El álgebra lineal numérica puede considerarse como el campo subordinado al álgebra lineal, en el sentido de que se basa en sus fundamentos teóricos para producir algoritmos útiles con fines prácticos. Mientras que el álgebra lineal ofrece principios abstractos y teoremas, el álgebra lineal numérica se esfuerza en aplicarlos eficientemente utilizando medios computacionales.

Aplicaciones del Mundo Real

Aplicaciones del Álgebra Lineal Numérica

Procesamiento de Imágenes y Señales

El álgebra lineal numérica desempeña un papel esencial en el procesamiento de imágenes y señales. Técnicas como la Descomposición en Valores Singulares (SVD) proporcionan funciones esenciales, incluyendo la compresión de imágenes, reducción de ruido y extracción de características, ayudando a procesar eficientemente grandes volúmenes de datos para aplicaciones como la imagen médica o la fotografía digital.

Ingeniería Financiera

La ingeniería financiera utiliza el álgebra lineal numérica para modelar y resolver problemas relacionados con la gestión de riesgos, la optimización de carteras y la fijación de precios de derivados. Los algoritmos de cálculo matricial juegan un papel integral en la simulación de mercados financieros y la toma de decisiones de inversión informadas.

Dinámica de Fluidos

El álgebra lineal numérica desempeña un papel esencial en la dinámica de fluidos al resolver ecuaciones diferenciales parciales que rigen el flujo de fluidos; al mismo tiempo, los métodos de elementos finitos y los solucionadores iterativos ayudan a los ingenieros a modelar comportamientos complejos de fluidos para cumplir con los estándares ambientales.

Aplicaciones del Álgebra Lineal

Animación por Computadora

El álgebra lineal se encuentra en el núcleo de la animación por computadora, utilizada para modelar y manipular geometrías de objetos mediante técnicas como transformaciones, rotaciones y escalados. Con tales métodos, surgen animaciones realistas en películas o videojuegos, así como efectos visuales impresionantes que dan vida a sus guiones gráficos.

Aprendizaje Automático

El álgebra lineal se encuentra en el núcleo del aprendizaje automático, proporcionando algoritmos para el análisis de datos y el reconocimiento de patrones. Entender conceptos como espacios vectoriales, factorizaciones matriciales y valores propios es primordial al desarrollar métodos como el Análisis de Componentes Principales o la Descomposición en Valores Singulares (SVD).

Referencia:

1. https://en.wikipedia.org/wiki/Linear_algebra

2. https://en.wikipedia.org/wiki/Numerical_linear_algebra