¿Qué es un valor p?

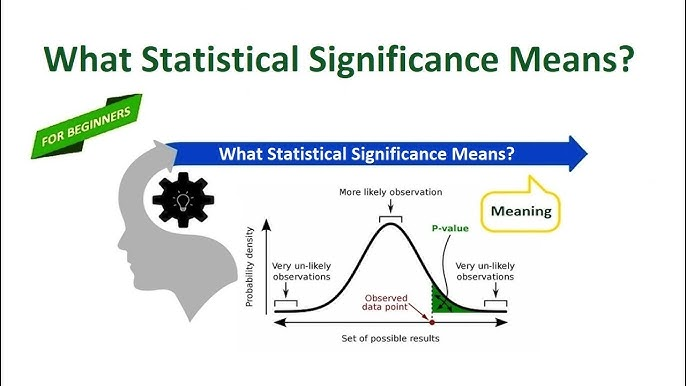
Los datos juegan un papel esencial en nuestra vida cotidiana, ayudándonos a evaluar la probabilidad de varios eventos. Xiaoming quería probar si la moneda en su posesión era realmente justa realizando un experimento: lanzándola diez veces. Xiaoming puede comenzar a sospechar que su moneda tiene un sesgo inherente que hace que 8 de cada 10 lanzamientos caigan de cara, indicando una aparente no aleatoriedad que no puede simplemente explicarse como aleatoriedad. En tales momentos, el valor P se convierte en un concepto poderoso e indispensable en la estadística. El valor P nos permite cuantificar la probabilidad de resultados inesperados o situaciones extremas al ofrecernos una herramienta de evaluación para ver si los resultados pueden atribuirse a la aleatoriedad. Al proporcionar una medida tan precisa, nos ayuda a tomar decisiones más racionales e informadas basadas en datos. Entonces, ¿qué es exactamente un valor P, por qué la estadística moderna depende de él y cómo puede guiar los procesos de toma de decisiones? Vamos a profundizar.

Concepto Básico del Valor P

Definición y Concepto Fundamental del Valor P

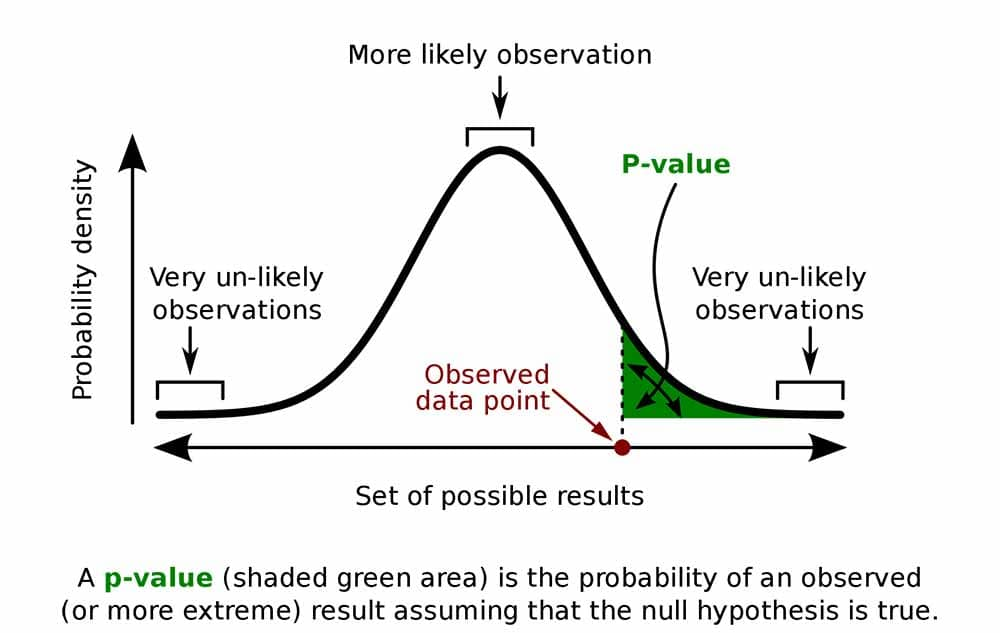
El valor P, también conocido como valor de probabilidad, es una métrica integral utilizada en la prueba de hipótesis estadística. Representa el riesgo de que resultados tan extremos o más extremos que los observados ocurran asumiendo que se mantiene la hipótesis nula. Dicho esto de manera simple, cuanto más bajo sea el valor P, menos probable es que lo observado se deba únicamente al azar.

Relación Entre el Valor P y la Probabilidad

Un valor P es una medida de probabilidad utilizada para evaluar la rareza de los resultados de datos y generalmente varía entre 0 y 1:

Tales valores proporcionan una fuerte evidencia en contra de aceptar la hipótesis nula; un resultado así bajo esta hipótesis casi nunca ocurriría y, por lo tanto, sugiere evidencia en contra de su aceptación.

Un valor P cercano a 1 indica que los resultados bajo la hipótesis nula son altamente probables, lo que dificulta que alguien la refute.

Ejemplo: Una Explicación Intuitiva del Valor P  

Imagina un aula en la que tanto niños como niñas usan gafas de una marca con la misma frecuencia; después de muestrear aleatoriamente este grupo, un investigador encuentra una proporción ligeramente mayor de niños usando esta marca de lo que se esperaba del muestreo aleatorio solamente. Después de calcular su valor P, este investigador determina que "si las probabilidades verdaderas de usar gafas entre géneros fueran iguales, un resultado tan extremo del muestreo aleatorio solo ocurriría el 3% del tiempo,"-lo que implica que los niños pueden realmente usar esa marca más frecuentemente que las niñas.

El Valor P y la Prueba de Hipótesis  

Hipótesis Nula e Hipótesis Alternativa  

Definiciones y Roles

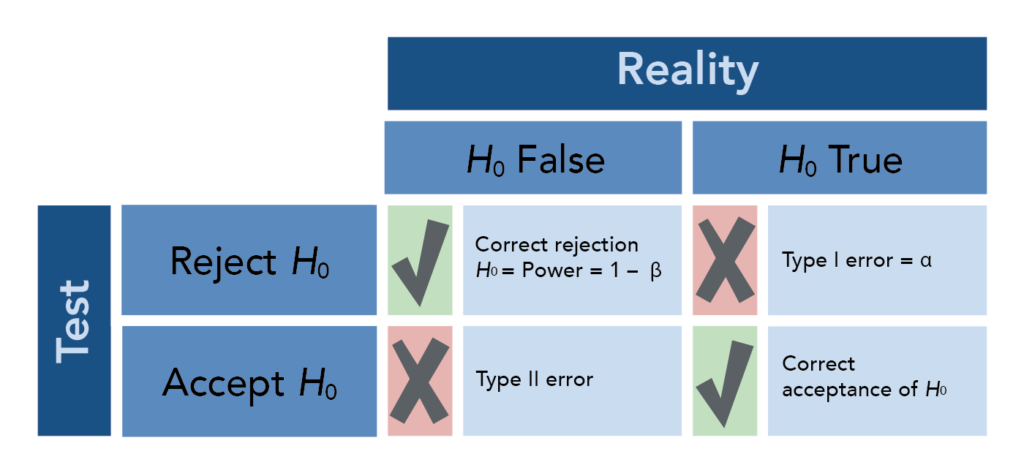
La prueba estadística emplea la prueba de hipótesis estadística en la cual dos supuestos, conocidos como H0 (o la "suposición por defecto") y una hipótesis alternativa H1, sirven para demostrar que no hay diferencia significativa en un experimento. Luego, los estadísticos utilizan el valor P para evaluar si hay suficiente evidencia en contra de rechazar H0.

Ejemplo: al probar la eficacia de un nuevo medicamento, la hipótesis nula podría declarar, "No hay diferencia significativa en la eficacia entre este nuevo medicamento y su predecesor," mientras que la hipótesis alternativa propondría "El nuevo medicamento es significativamente más efectivo." Dependiendo del análisis de datos experimentales y los cálculos del valor P, los investigadores pueden decidir si existe tal diferencia.

Papel del Valor P en la Prueba de Hipótesis

Nivel de Significación y Decisiones Estadísticas

El nivel de significación (α) establece el umbral para rechazar la hipótesis nula. Por ejemplo, si α se establece en 0.05 y tiene un valor P menor que este valor, entonces los resultados son estadísticamente significativos, y los investigadores pueden rechazar su hipótesis nula.

Interpretación con Diferentes Niveles de Significación

Diferentes niveles de significación representan diferentes niveles de tolerancia al riesgo al hacer conclusiones erróneas. Por ejemplo, los investigadores médicos que examinan la efectividad de un medicamento podrían requerir el uso de valores de significación más bajos (por ejemplo, 0.01) para minimizar cualquier posibilidad de rechazar incorrectamente hipótesis nulas.

Ejemplo: Valor P y Decisiones Estadísticas  

Imagina esto: al realizar pruebas para medir la eficacia de un nuevo medicamento, el análisis de datos genera un valor P de 0.03 mientras que el nivel de significación (α) se encuentra en 0.05. Como P es menor que α, los investigadores concluyen que sus resultados son estadísticamente significativos y rechazan su hipótesis nula en favor de la hipótesis de que tal vez este nuevo medicamento podría realmente funcionar efectivamente.

¿Cómo calcular un valor P?

Métodos básicos de cálculo

Integración del área de la curva de distribución de probabilidad

El cálculo de los valores P generalmente se basa en la teoría estadística y las distribuciones de probabilidad. Integrar las áreas bajo una curva de distribución normal estándar, por ejemplo, puede ayudar a estimar probabilidades asociadas con estadísticas de prueba; tales áreas corresponden a valores P.

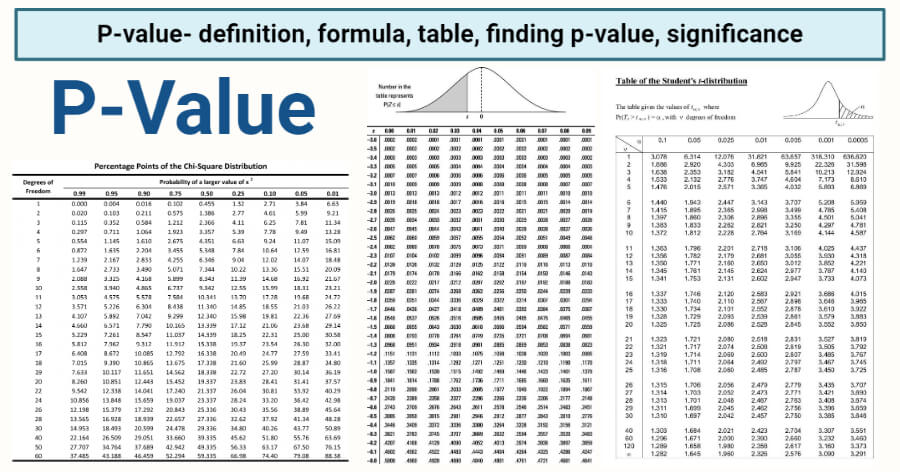
Uso de tablas de valores P

Los estadísticos han desarrollado tablas estándar de valores P para facilitar la búsqueda rápida de intervalos aproximados de valores P asociados con estadísticas de prueba específicas (por ejemplo, pruebas t y pruebas chi-cuadrado). Estas permiten una referencia rápida al realizar estas pruebas comunes (incluyendo pruebas t y pruebas chi-cuadrado).

Herramientas de software y cálculo automatizado

Aprovechando software como R, SPSS, etc.

El software estadístico moderno ha simplificado enormemente los cálculos de valores P gracias a innovaciones tecnológicas, por ejemplo, el lenguaje de programación R ahora puede realizar pruebas y proporcionar el valor P en una sola línea de código; haciendo el análisis de datos complejo mucho más accesible y eficiente que antes.

Conceptos erróneos comunes sobre los valores P y interpretaciones correctas

Conceptos erróneos sobre los valores P

Un valor P no prueba directamente una hipótesis

Un valor P extremadamente pequeño no indica que una hipótesis alternativa sea realmente correcta; más bien, indica que, bajo la suposición de una hipótesis nula, sus datos actuales son poco probables de haber ocurrido solo por casualidad y no sirven como apoyo directo para la hipótesis alternativa.

Valor P pequeño ≠ alta confianza

Aunque un valor P bajo proporciona evidencia contra la hipótesis nula, no cuantifica la probabilidad de que sea verdadera; se necesita generalmente un contexto adicional y validación de datos antes de llegar a conclusiones confiables.

Consejos para una comprensión correcta de los valores P

Interpretación de valores P desde una perspectiva de probabilidad

Un valor P es un concepto integral en estadísticas que mide la probabilidad de que los datos actuales, o algo más extremo, ocurran bajo una suposición llamada hipótesis nula. Así ayuda a evaluar la aleatoriedad. Un valor P más pequeño indica resultados menos probables de lo esperado bajo la hipótesis nula - lo que fomenta pruebas adicionales o revisiones basadas en esta nueva información.

Interpretación de valores P en escenarios de la vida real

Para usar correctamente los valores P, es imperativo considerar su uso dentro de su diseño experimental, tamaño de la muestra y otras consideraciones relevantes. No debe ocurrir una interpretación del valor P de forma aislada de su contexto circundante.

La Relación Entre Valores P y Otros Métricas Estadísticas  

Valores P y Niveles de Significancia (Alfa) 

Definición y Configuración de Niveles Alfa  

El nivel alfa o nivel de significancia sirve como el umbral máximo de probabilidad utilizado para tomar decisiones sobre rechazar hipótesis nulas y sugerir efectos que no podrían haber surgido solo debido al azar. Su valor más frecuentemente empleado en análisis estadístico se establece en 0.05; esto significa que si el valor P cae por debajo de este umbral, el resultado se considera estadísticamente significativo y, por lo tanto, lleva al rechazo de la hipótesis nula y sugiere mecanismos causales poco probables de los efectos observados.

Ejemplo: Comparación Entre Valores P y Alfa  

Imagina esto: al investigar la eficacia de un medicamento, un experimento arroja un valor P de 0.03 con un nivel alfa de 0.05; dado que 0.03 está por debajo de este umbral, se rechaza la hipótesis nula inferiendo que su uso podría ser efectivamente eficaz.

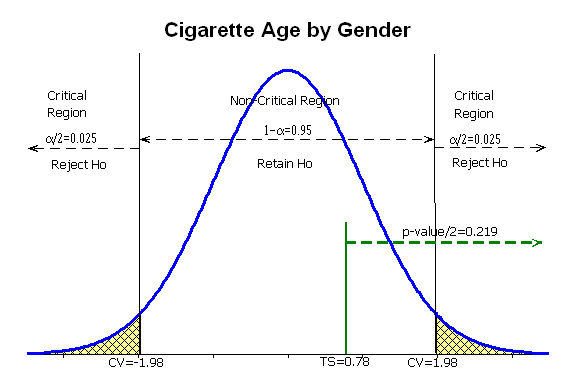
Valores P y Valores Críticos  

Valores Críticos en Pruebas Como F-Tests

Valores críticos juegan un papel integral en pruebas estadísticas como F-tests al proporcionar puntos de referencia para medir la significancia. Cuando el valor F calculado supera este umbral de valor crítico, esto significa que las diferencias observadas entre varianzas de grupos no pueden haber ocurrido solo por azar; así ayudando a los investigadores a tomar decisiones fundamentadas sobre la prueba de la hipótesis nula o intervenciones realizadas en los estudios.

Ejemplo: Decisiones Basadas en Valores Críticos y Valores P  

Ciertas pruebas estadísticas, como ANOVA, que emplean estadísticas F, utilizan un valor crítico para establecer si sus resultados son estadísticamente significativos. Cuando los valores F superan este umbral crítico, un resultado se considera estadísticamente significativo y debe ser interpretado con valores P para proporcionar una comprensión profunda de tus datos y conclusiones precisas sobre cualquier efecto que se esté estudiando.

Valores P y Significado Estadístico

Juzgando el Significado Estadístico

¿Qué es el Significado Estadístico?

El significado estadístico mide si una diferencia observada probablemente no ha surgido solo por casualidad. Cuando el valor P cae por debajo de un umbral de significación establecido (por ejemplo, 0.05), esto indica que la variación es probablemente atribuible a efectos reales en lugar de ruido aleatorio.

Ejemplo: Evaluando la Significación en Resultados Experimentales

Imagina esto: los resultados de un experimento de psicología demuestran una terapia alternativa efectiva con un impresionante valor P de 0.01. Como este umbral está muy por debajo de los niveles típicos de significancia (como 0.05), los investigadores podrían concluir que hubo un efecto genuino de la terapia, pero deben ser cautelosos para detectar posibles factores de confusión e influencias negativas que podrían oscurecer cualquier correlación positiva.

Valores P y Apoyo a las Hipótesis de Investigación

Ejemplo: Entendiendo Cómo los Valores P Apoyan una Hipótesis

Un hallazgo importante de un estudio reveló un valor P de 0.001, lo que significa que incluso bajo la hipótesis nula, existe un 0.1% de probabilidad de observar un resultado tan extremo, proporcionando un fuerte apoyo para una hipótesis alternativa.

Combinando Valores P con Otros Métricas Estadísticas

Aunque el valor P es una herramienta indispensable en el análisis estadístico, usarlo solo puede llevar a malentendidos y errores en las conclusiones. Los investigadores deben combinar varios métricas - tamaño del efecto, calidad del diseño experimental y tamaño de la muestra entre ellas - junto al valor P para obtener resultados más sólidos.

Limitaciones de los Valores P y Tendencias Futuras en su Aplicación

Limitaciones de los Valores P

Capacidad Limitada para Inferir Causalidad

Los valores P tienen una limitación clave que restringe su utilidad; solo indican significancia estadística y no pueden inferir directamente relaciones causales entre variables. Incluso en estudios observacionales donde valores P pequeños pueden indicar significancia estadística, esto no asegura conclusiones causales precisas.

Influencia del Tamaño de Muestra sobre los Valores P

Los tamaños de muestra grandes a menudo llevan a valores P extremadamente pequeños, lo que podría simplemente reflejar un aumento del poder estadístico en lugar de su significancia práctica. Por lo tanto, es imperativo que se consideren los tamaños del efecto junto con los valores P al realizar análisis estadísticos.

Tendencias Futuras y Avances en la Aplicación de Valores P

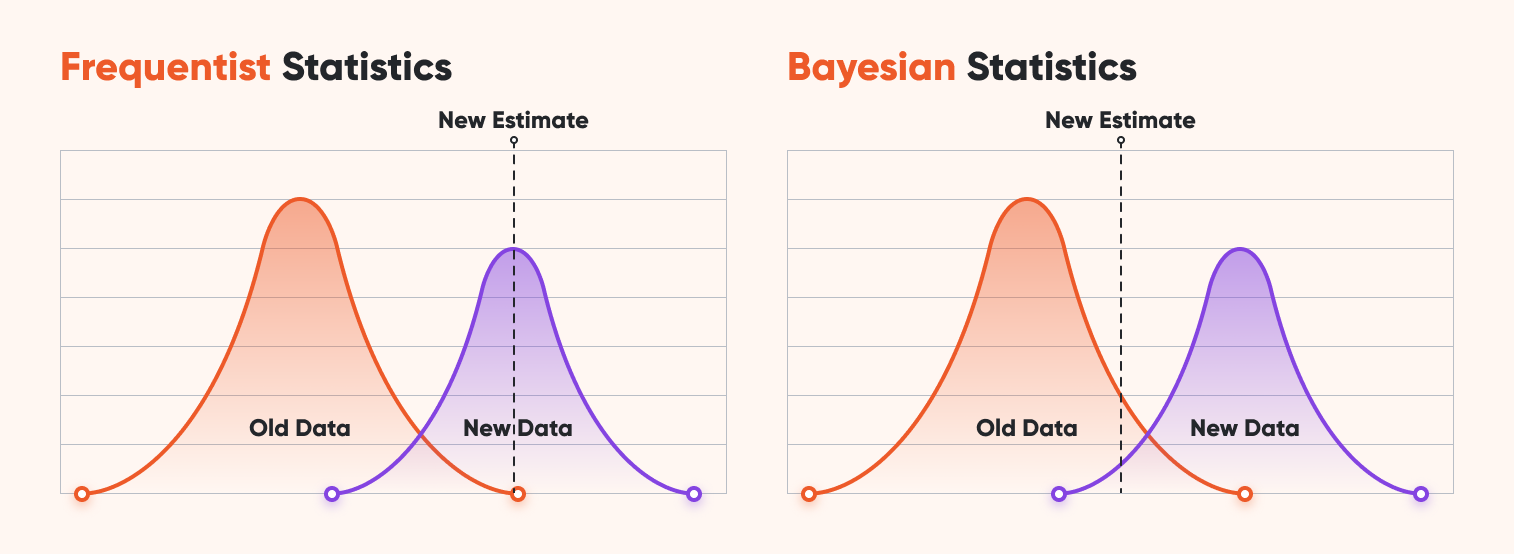
Integración con Métodos Estadísticos Bayesianos

Un número creciente de investigadores está empleando el análisis de probabilidad posterior bayesiana además de los valores P en sus procesos de evaluación. Esto proporciona análisis más matizados en relación con juzgar la credibilidad de las hipótesis en comparación con las pruebas de significancia tradicionales.

Ajustes para Pruebas Múltiples para Mejorar la Interpretación

Los investigadores que realizan pruebas de hipótesis múltiples, como la investigación genética, a menudo recurren a ajustes de Bonferroni como una forma de alterar su umbral de valor P y disminuir las tasas de falsos positivos a la vez que mejoran la credibilidad de los hallazgos y establecen estándares más altos para entender los valores P.

Estudios de Caso del Mundo Real de Valores P

Ejemplo: Inversión y Comparación de Indicadores de Mercado

Un ejemplo de nuestro banco de preguntas: un inversor que afirma que su cartera se compara favorablemente con un indicador de mercado S&P 500, por ejemplo. Después de realizar un análisis estadístico sobre esta afirmación, los investigadores llegan a un valor P de 0.02, que está por debajo del nivel de significancia de 0.05 y, por lo tanto, proporciona información significativa para futuras decisiones de inversión.

Ejemplo: Aplicaciones de los Valores P en Investigación Científica y Médica

Los valores P juegan un papel esencial en la evaluación médica de nuevos medicamentos. Tras realizar ensayos clínicos, los investigadores pueden encontrar que un grupo muestra una tasa de curación significativamente mayor que su grupo de control, obteniendo un valor P de 0.001. Esto sugiere que solo había un 0.1% de probabilidad, bajo la hipótesis nula, de que existieran esos datos y fortalece la evidencia a favor de nuevos medicamentos efectivos. Este resultado respalda firmemente su afirmación.

Los valores P, una herramienta esencial en el análisis estadístico, ofrecen a los investigadores una medida cuantitativa de la significancia de los resultados de los datos. Sin embargo, una dependencia excesiva en los valores P para la toma de decisiones puede conducir a interpretaciones erróneas o pasarse por alto aspectos importantes del diseño del estudio. De cara al futuro, la integración de otras técnicas estadísticas, como medidas de tamaño de efecto, enfoques bayesianos y correcciones para múltiples hipótesis, se convertirán en elementos clave para mejorar el rigor científico y la precisión de los análisis estadísticos. Comprender y usar correctamente los valores P son partes integrales de la toma de decisiones basada en datos en proyectos de investigación científica, análisis de inversión y aplicaciones médicas. ¡Comprender y usar los valores P adecuadamente es integral para tomar decisiones basadas en datos!

referencia:

https://en.wikipedia.org/wiki/P-value

https://en.wikipedia.org/wiki/Statistical_significance

https://en.wikipedia.org/wiki/Null_hypothesis