¿Qué es una Secuencia?

¿Has experimentado este enigma: cada día ahorras dinero, pero calcular su total después de un mes parece terriblemente complejo? Imagina un estanque donde solo aparece una hoja de loto el día 1, dos el día 2, cuatro el día 3, seis el día 4... En cada día sucesivo después, su número se duplica... ¿Puedes predecir cuántas aparecerán para el día 10? Estos problemas involucran secuencias. La secuencia se define como una serie ordenada de números organizada según reglas específicas, que no solo tiene aplicaciones directas en la vida cotidiana sino que también se encuentra en las matemáticas, la informática, la previsión económica y la investigación en inteligencia artificial. Entender las secuencias puede ayudarnos a resolver problemas basados en patrones más rápidamente y realizar análisis más profundos. Siguiendo este artículo, obtendrás un conocimiento completo de las definiciones, clasificaciones, fórmulas y aplicaciones reales de las secuencias, descubriendo tanto su belleza lógica como su uso práctico.

Conceptos Fundamentales de las Secuencias

Qué es una Secuencia

Una secuencia es uno de los conceptos fundamentales en matemáticas, representando un conjunto ordenado de números arreglados según reglas o patrones específicos. Dicho de manera sencilla, una secuencia puede ser cualquier colección de números ordenados como 1, 2, 3, 4, 5. Estos números pueden seguir un patrón particular o incluso parecer aleatorios; sin embargo, lo que unifica a todas las secuencias es que a cada término se le asigna una posición específica, normalmente representada por números naturales como 1, 2, 3, 4, y así sucesivamente.

Las secuencias han estado por mucho tiempo en el núcleo de los estudios matemáticos - desde matemáticas elementales con tablas numéricas hasta estudios avanzados usando secuencias complejas como herramientas matemáticas esenciales para su aplicación y desarrollo. Las secuencias pueden ser finitas (número limitado de términos incluidos), infinitas o intermedias y juegan un papel esencial en el desarrollo y aplicación del conocimiento sobre sistemas matemáticos.

Definición y Características

Las secuencias tienen definiciones y rasgos específicos:

1. Orden: Cada término en una secuencia ha sido designado un número de índice o número de término que usualmente toma la forma de números naturales como su representación.

2. Regla de Generación: El valor de cada término está determinado por una regla explícita o implícita que puede incluir relaciones recursivas y/o ser expresada explícitamente.

3. Finita o Infinita: Las secuencias pueden contener números finitos de términos (por ejemplo, los primeros 10 términos), o podrían incluir una secuencia crecientemente ilimitada (es decir, una secuencia crecientemente infinita).

4. Generalidad: Las secuencias pueden representar desde patrones simples con estructuras fácilmente reconocibles hasta fenómenos más complicados como el movimiento físico y tendencias financieras - haciéndolas poderosas herramientas matemáticas que sirven ambos propósitos igualmente bien.

Representación de las Secuencias

Las secuencias pueden ser representadas de diferentes maneras dependiendo de su complejidad y las necesidades de los investigadores, incluyendo:

Fórmula Explícita

Una fórmula explícita (o de forma cerrada) expresa directamente cualquier término en una secuencia con expresiones matemáticas; por ejemplo, en una secuencia aritmética:

\(a_n = a_1 + (n - 1)d\)

Aquí, \(a_1\) representa el primer término mientras que \(d\) es su diferencia común, y \(n\) significa su posición. Usando esta ecuación, se pueden calcular rápida y eficientemente cualquier término subsecuente usando solo el conocimiento de los existentes.

Fórmula Recursiva

Las fórmulas recursivas se utilizan para definir cada término según los anteriores, como en la secuencia de Fibonacci (que usa esta fórmula recursiva), como

\(a_n = a_{n-1} + a_{n-2} \quad (n \geq 3, a_1 = 1, a_2 = 1)\)

Las relaciones recursivas pueden ser particularmente útiles en secuencias donde cada término depende de los otros para propósitos de definición.

Símbolos Especiales y Tablas Numéricas

Los matemáticos usan símbolos especiales o tablas numéricas para simplificar la representación de secuencias, tales como:

1. Denotar números secuencialmente usando \(\{a_n\}\) o \((a_n)\) símbolos.

2. Mostrar términos en tablas que alinean sus valores con índices específicos para aumentar claridad.

Estos tres enfoques juntos ofrecen métodos versátiles para analizar y expresar secuencias.

La Diferencia Entre Secuencias y Series  

Las secuencias y series son dos conceptos matemáticos relacionados, pero cada uno tiene una importancia distinta. En pocas palabras, secuencia se refiere a una lista ordenada de números mientras que las series enfatizan su suma. A continuación, más información sobre sus diferencias:

1. Concepto Básico: Una secuencia se refiere a un arreglo ordenado y secuencial de términos individuales, por ejemplo, determinando su valor cuando se combinan, mientras que una serie se refiere a la acumulación acumulativa. Un ejemplo de una secuencia podría incluir 1, 2, 3, 4, 5...

Serie Correspondiente: \(1 + 2 + 3 + 4 + 5 + \dots\)  

2. Representación Matemática: Las secuencias a menudo pueden representarse usando notaciones anotativas como \(\{a_n\}\), que denotan la forma general de cada término sucesivo de una secuencia, mientras que las series se expresan usando notación de sumatoria \(\Sigma\):

\(S_n = \sum_{k=1}^{n} a_k\)  

3. Perspectiva de Estudio: Las secuencias se enfocan en estudiar los valores individuales de los términos y sus relaciones entre ellos, mientras que las series se enfocan en sumas acumuladas con propiedades como convergencia o divergencia.

4. Aplicaciones: Las secuencias se utilizan para pronosticar patrones individuales como el análisis de series temporales, mientras que las series son útiles en cálculos acumulativos como la acumulación de intereses o la estimación de errores en cálculos numéricos.

En resumen, una secuencia puede verse como "punto a punto", mientras que las series expanden esta idea con técnicas de resumen; ambos proporcionan herramientas complementarias pero distintas para resolver problemas.

Tipos Comunes de Secuencias  

Tipos Básicos de Secuencias  

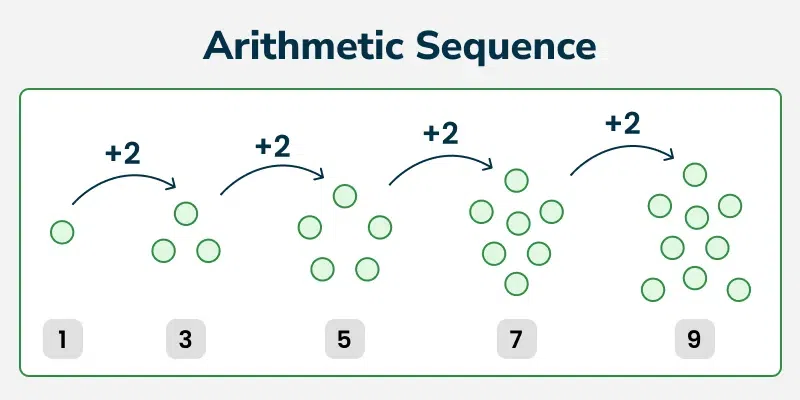
Secuencia Aritmética  

Una secuencia aritmética es uno de los tipos de secuencia básicos, caracterizado por tener una diferencia constante, conocida como "diferencia común," entre términos consecutivos. Para escribir su fórmula de término general:

\(a_n = a_1 + (n - 1)d\)  

Donde \(a_1\) representa el primer término, \(d\) representa su diferencia común y \(n\) denota su índice de término.

Un ejemplo del banco de preguntas: Una secuencia aritmética que consiste en 2, 5, 8, 11... se conoce como una serie aritmética en la que su primer término es 2 y su diferencia común, 3. Las series aritméticas son a menudo utilizadas en muchos campos para ahorrar dinero a intervalos regulares de manera uniforme, aumentando los ahorros totales con el tiempo según un patrón uniforme.

Secuencia Geométrica  

Las secuencias geométricas son otro tipo clásico de secuencia en la que la razón entre términos consecutivos permanece constante; este valor fijo se suele llamar razón común. Una forma general para tal enfoque podría verse como sigue:

\(a_n = a_1 \cdot r^{n-1}\)  

Donde \(a_1\) representa el primer término, \(r\) es su razón común y \(n\) es su índice de término.

Ejemplo: La secuencia 3, 6, 12, 24... es un ejemplo de una secuencia geométrica con 3 como su primer término y 2 como su razón común. Las secuencias geométricas pueden ser herramientas útiles en el estudio del crecimiento o decrecimiento exponencial, como el crecimiento de la población o la desintegración radiactiva.

Tipos Especiales de Secuencias  

Secuencia Cuadrática  

Las secuencias cuadráticas siguen un patrón en el que cada término de su secuencia puede determinarse usando una ecuación cuadrática, típicamente expresada como:

\(a_n = an^2 + bn + c\)  

Donde \(a, b, c\) son constantes. Por ejemplo, la secuencia 1, 4, 9, 16, 25... es un ejemplo de una secuencia cuadrática; cada término corresponde a\(n^2\) de esta manera. Las secuencias cuadráticas suelen usarse como formas de representar el movimiento parabólico de objetos como las trayectorias de proyectiles.

Secuencia Armónica  

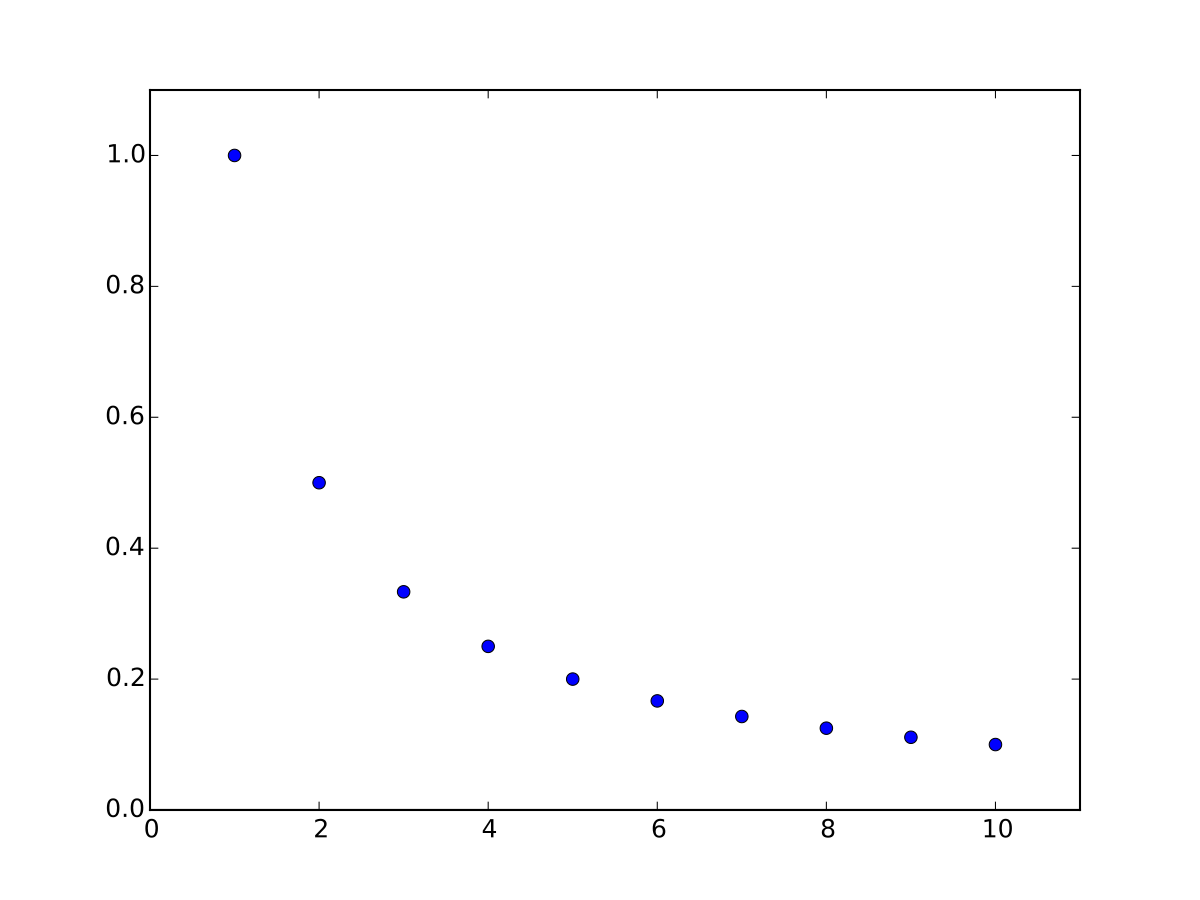
Las secuencias armónicas se definen por términos que representan recíprocos de números naturales, usando esta fórmula general:

\(a_n = \frac{1}{n}\)  

Secuencias armónicas como 1, 1/2, 1/3... pueden verse frecuentemente al analizar el rendimiento de redes o problemas de asignación de recursos.

Secuencia de Números Cuadrados  

Las secuencias de números cuadrados, definidas como aquellas donde cada término corresponde a su índice al cuadrado, pueden representarse usando esta expresión:

\(a_n = n^2\)  

Un ejemplo sería 1, 4, 9, 16, 25... que forma tal secuencia y a menudo se utiliza en arquitectura y diseño para modelar diseños o estructuras basadas en cuadrados.

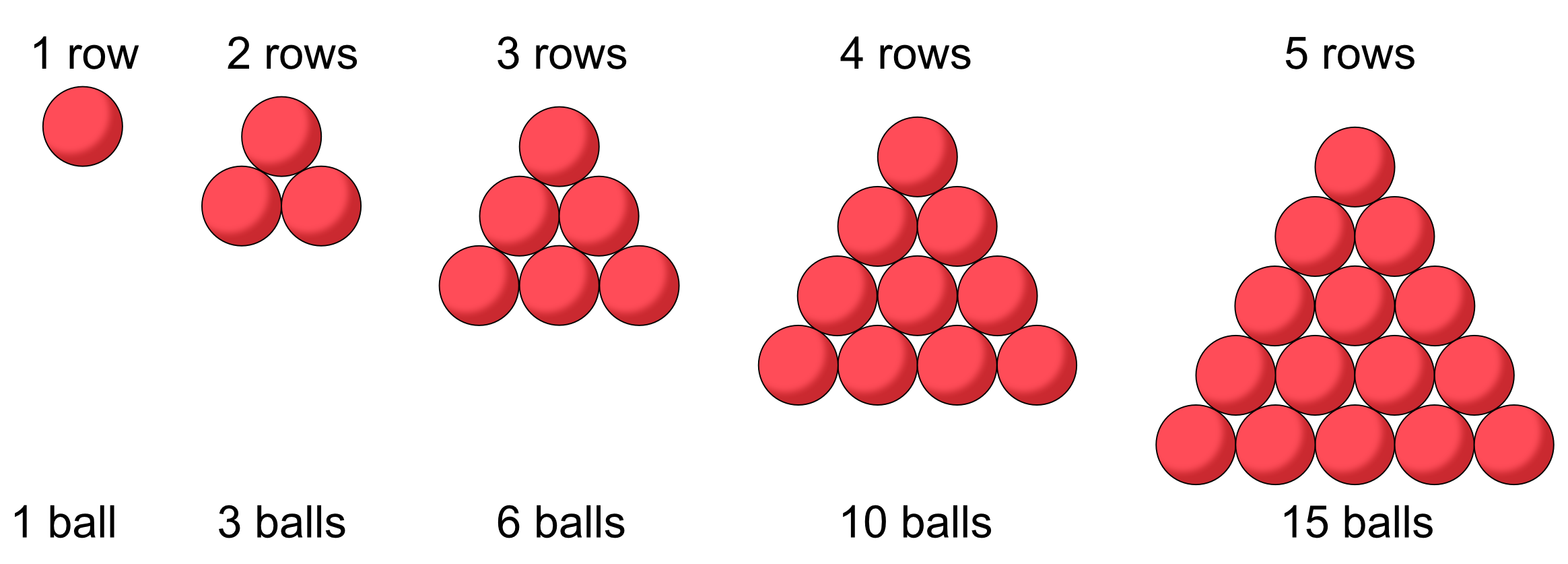
Secuencia Triangular  

Las secuencias triangulares pueden definirse como series de números que representan el número total de puntos encontrados dentro de un patrón triangular, usualmente representados como términos. Su fórmula de cálculo típicamente sigue este formato:

\(a_n = \frac{n(n+1)}{2}\)  

Ejemplo de secuencias triangulares es 1, 3, 6, 10, 15... Estas secuencias triangulares a menudo surgen en combinatoria al estudiar problemas de arreglos y combinaciones.

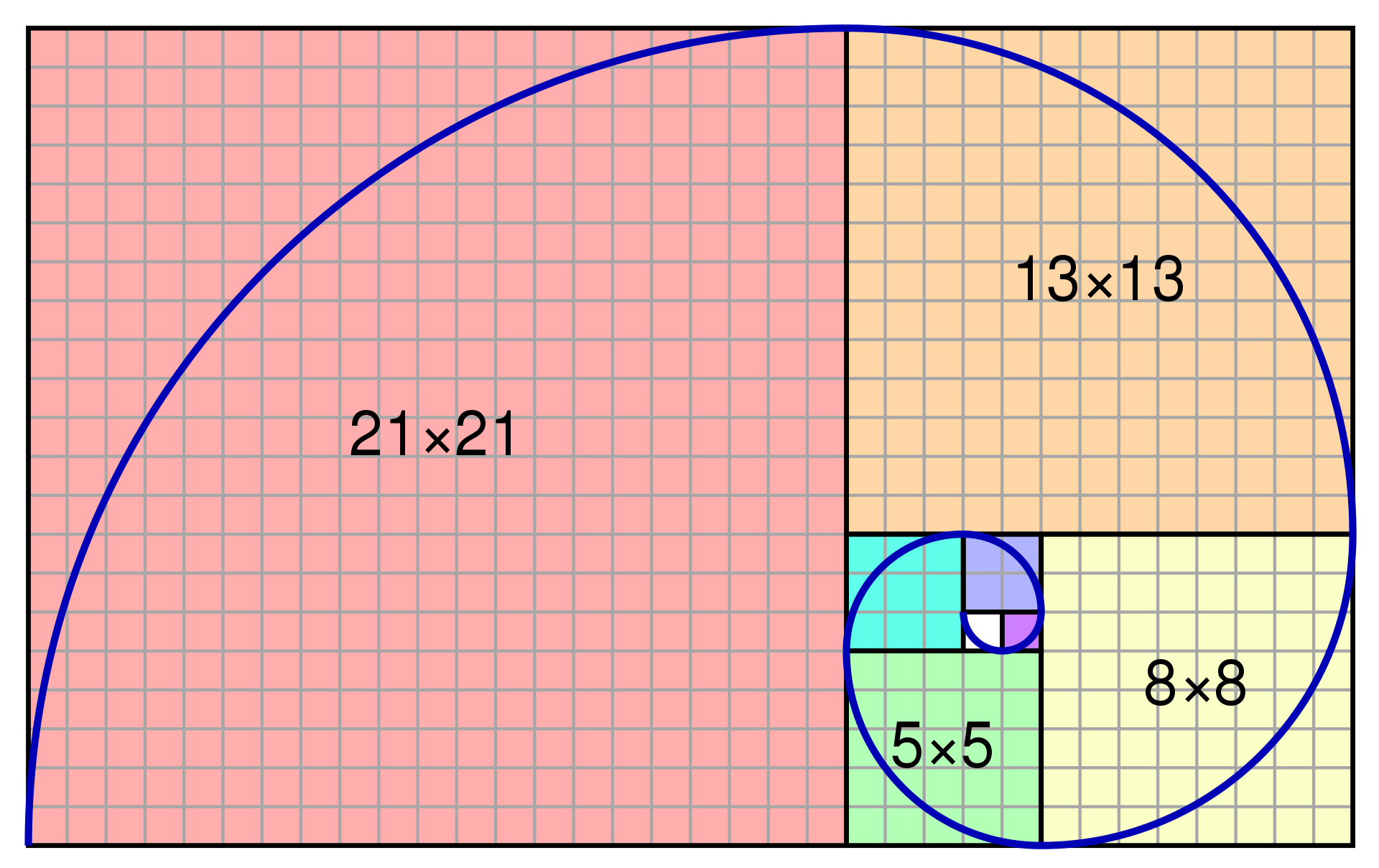
Secuencia de Fibonacci  

La secuencia de Fibonacci es una antigua secuencia matemática definida por su fórmula:

\(a_n = a_{n-1} + a_{n-2} \quad (n \geq 3, a_1 = 1, a_2 = 1)\)  

Una ilustración: la secuencia de Fibonacci comprende 1, 2, 3, 5, 8, 13... Esta expresión matemática tiene aplicaciones en disciplinas como la biología, economía y arte, así como en estudios como el análisis de la proporción áurea o patrones de crecimiento natural.

Patrones de Secuencias Extendidas  

Secuencias Doble Recursivas  

Las secuencias doble recursivas son más complicadas, donde cada término depende no solo de uno o dos términos anteriores, sino que puede involucrar recursión de múltiples pasos, por ejemplo:

\(a_n = a_{n-1} + 2a_{n-2} - a_{n-3}\)  

Estas secuencias complejas pueden verse a menudo al tratar con la creación de algoritmos o tareas de modelado avanzado.

Secuencias Generadas por Datos y Algoritmos 

Las secuencias impulsadas por algoritmos representan una expansión innovadora de las secuencias tradicionales. Los modelos de aprendizaje automático, por ejemplo, pueden generar secuencias basadas en reglas dinámicas extraídas de datos para producir fórmulas flexibles que se adaptan más fácilmente a patrones encontrados dentro de grandes conjuntos de datos que las fórmulas fijas.

Fórmulas y Métodos de Sucesiones

Fórmulas Comunes para Sucesiones

Fórmulas de Sucesiones Aritméticas

La fórmula general para una sucesión aritmética se puede expresar de la siguiente manera:\(a_n = a_1 + (n - 1)d\).

Además, se puede calcular la suma de los primeros \(n\) términos usando esta ecuación:

\(S_n = \frac{n}{2} \cdot (a_1 + a_n) \quad \text{o} \quad S_n = \frac{n}{2} \cdot [2a_1 + (n - 1)d]\)  

Estas fórmulas facilitan el cálculo de términos individuales o la suma de varios términos dentro de una sucesión aritmética.

Por ejemplo: Dada una sucesión aritmética con \(a_1 = 3\) y \(d = 2\), calcula tanto el 5º término como su suma:

1. Término general: \(a_5 = 3 + (5-1) \cdot 2 = 11\)  

2. Suma de los primeros cinco términos\(S_5 = \frac{5}{2} \cdot (3 + 11) = 35\)  

Fórmulas de Sucesiones Geométricas

La fórmula general para sucesiones geométricas es la siguiente:

\(a_n = a_1 \cdot r^{n-1}\)  

La suma de los primeros \(n\) términos se puede expresar de la siguiente manera:\(S_n = \frac{a_1 (1 - r^n)}{1 - r}, \quad r \neq 1\)  

Para sucesiones donde \(|r| < 1\) y donde \(n\) se aproxima al infinito, su suma infinita se puede escribir como:

\(S_\infty = \frac{a_1}{1 - r}\)  

Por ejemplo: Dada una sucesión geométrica con ( a_1 = 2 \) y \(r = 3\), Calcula el 4º término y la suma de los primeros 4 términos

1. Término general: \(a_4 = 2 \cdot 3^{4-1} = 54\)  

2. Suma de los primeros 4 términos: \(S_4 = \frac{2(1-3^4)}{1 - 3} = 80\)  

Fórmulas para Sucesiones Especiales

Fórmula de la Sucesión de Números Cuadrados

La suma de los primeros \(n\) términos en una sucesión de números cuadrados se da por:  

\(S_n = \frac{n(n+1)(2n+1)}{6}\)  

Ejemplo: Para la sucesión de números cuadrados 1, 4, 9, 16..., encuentra la suma de los primeros 4 términos:  

\(S_4 = \frac{4 \cdot 5 \cdot 9}{6} = 30\)  

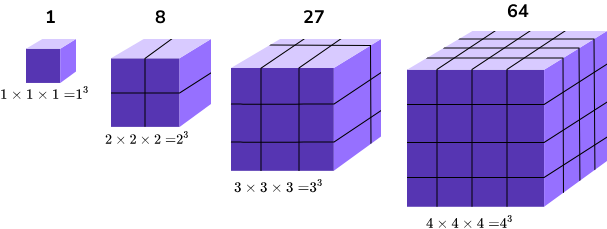
Fórmula de la Sucesión de Números Cúbicos

La suma de los primeros \(n\) términos en una sucesión de números cúbicos se da por:  

\(S_n = \left( \frac{n(n+1)}{2} \right)^2\)  

Ejemplo: Para la sucesión de números cúbicos 1, 8, 27, 64..., encuentra la suma de los primeros 3 términos:  

\(S_3 = \left( \frac{3 \cdot 4}{2} \right)^2 = 36\)  

Fórmula de la Sucesión Triangular

El término general para una sucesión triangular es:  

\(a_n = \frac{n(n+1)}{2}\)  

La suma de los primeros \(n\) términos se expresa como:  

\(S_n = \frac{n(n+1)(n+2)}{6}\)  

Ejemplo: Para la sucesión triangular 1, 3, 6, 10, encuentra la suma de los primeros 4 términos:  

\(S_4 = \frac{4 \cdot 5 \cdot 6}{6} = 20\)  

Fórmula de la Sucesión de Fibonacci

La sucesión de Fibonacci se puede expresar utilizando una fórmula de forma cerrada (Fórmula de Binet):  

\(a_n = \frac{\phi^n - \psi^n}{\sqrt{5}}\)  

Donde \(\phi = \frac{1 + \sqrt{5}}{2}\) y \(\psi = \frac{1 - \sqrt{5}}{2}\).  

Esta fórmula ilustra que incluso las sucesiones recursivas pueden tener expresiones explícitas obtenidas mediante técnicas matemáticas avanzadas.

Fórmula de la Sucesión Armónica

Las sucesiones armónicas tienen la siguiente forma general:

\(a_n = \frac{1}{n}\)  

Su suma se puede expresar como:

\(H_n = 1 + \frac{1}{2} + \frac{1}{3} + \ldots + \frac{1}{n}\)  

Los números armónicos desempeñan un papel clave en el análisis numérico y la estimación asintótica.

Generalización y Derivación de Fórmulas

Conversión de Fórmulas Explícitas y Recursivas

Las fórmulas explícitas y recursivas a menudo se pueden convertir entre sí, por ejemplo, al considerar una sucesión aritmética con su fórmula recursiva:

\(a_n = a_{n-1} + d \quad (a_1 = 1)\) ,

La versión explícita se puede producir entonces:

\(a_n = a_1 + (n-1)d\)  

Esta conversión implica el análisis de patrones acumulativos. Es aplicable a sucesiones más complejas.

Generación Algorítmica de Fórmulas de Sucesiones

La tecnología moderna facilita la derivación automática de fórmulas de sucesiones a través de algoritmos. El análisis de regresión o los modelos de aprendizaje automático, por ejemplo, pueden detectar patrones ocultos dentro de grandes conjuntos de datos para generar automáticamente fórmulas recursivas o explícitas, una capacidad invaluable en el procesamiento de datos a gran escala y predicciones en tiempo real.

Aplicaciones y Usos Prácticos de las Secuencias  

Encontrar Términos Faltantes en una Secuencia  

Método de Observación de Patrones  

La observación de patrones implica analizar los términos conocidos de una secuencia para discernir su regla subyacente y extrapolar los términos faltantes basados en esta regla. Por ejemplo, en una secuencia que consta de 2, 4, 6X 10, el patrón observado muestra una diferencia común aparente de 2, por lo que extrapolando esa regla se llegaría a la conclusión de que su término faltante, en este caso\(X\), es igual a 8. Este enfoque funciona bien al tratar con secuencias simples y estructuradas.

Uso de Fórmulas de Retroceso  

Las fórmulas de retroceso pueden ayudar a desentrañar secuencias complejas deduciendo términos faltantes. Al crear una fórmula de término abstracto o una relación recursiva, se puede ingresar su ubicación y valor de cualquier término faltante para deducir su existencia y valor.

Ejemplo: Para secuencias geométricas con \(a_1 = 3\), \(r = 2\), pero falta el 4º término, usa esta fórmula general:

\(a_4 = a_1 \cdot r^{4-1} = 3 \cdot 2^3 = 24\)  

Este enfoque resuelve eficientemente términos desconocidos incluso en secuencias complejas o grandes.

Integrando Secuencias con la Tecnología Moderna  

El Papel de las Secuencias en el Análisis de Datos  

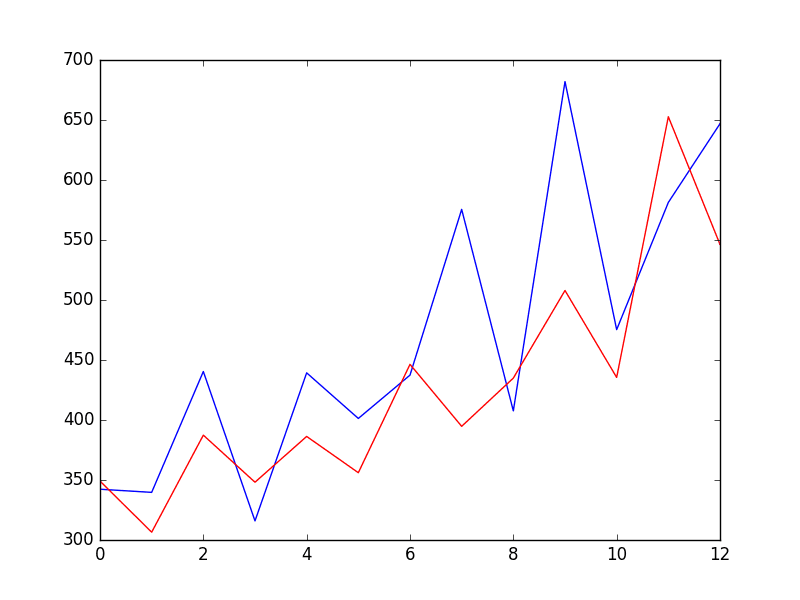
Las secuencias se utilizan comúnmente al analizar datos de series temporales, incluidos cambios de temperatura, movimientos del mercado de valores y rendimiento de ventas a lo largo del tiempo. Reconociendo una secuencia subyacente y haciendo predicciones sobre su comportamiento en futuros eventos de series temporales como temperaturas o cifras de ventas, los modelos ARIMA (Auto-Regressive Integrated Moving Average) utilizan datos de series temporales como herramientas predictivas en la previsión de información dependiente del tiempo y apoyan los procesos de toma de decisiones financieras y económicas.

Las secuencias juegan un papel fundamental en el análisis estadístico, proporcionando representaciones eficientes para distribuciones uniformes y normales. La investigación de patrones de secuencia permite a los analistas descubrir tendencias ocultas dentro de los conjuntos de datos mientras aumentan la precisión predictiva y las habilidades para resolver problemas.

Modelado de Secuencias en IA y Aprendizaje Automático  

Las secuencias desempeñan un papel esencial en la inteligencia artificial y el aprendizaje automático, particularmente para datos dependientes del tiempo. El Procesamiento de Lenguaje Natural (NLP), por ejemplo, depende en gran medida del modelado secuencial para analizar la entrada del usuario y generar respuestas; los sistemas de recomendación aprovechan las secuencias de actividad del usuario como indicadores predictivos para sugerir productos o contenidos relevantes a esas preferencias.

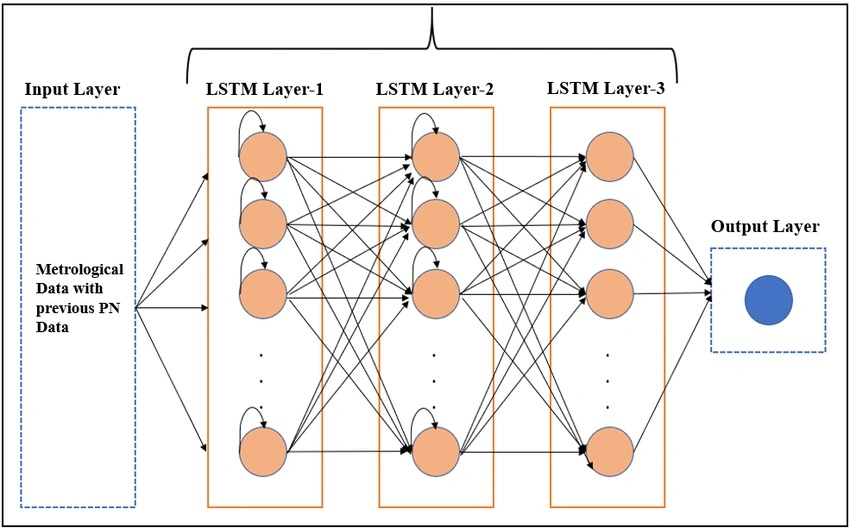
Las redes de Memoria a Largo Corto Plazo (LSTM), un ejemplo de Redes Neuronales Recurrentes (RNNs), fueron específicamente desarrolladas para procesar datos secuenciales para detectar relaciones interdependientes a lo largo del tiempo. Además, la teoría de secuencias es un componente clave para los modelos de aprendizaje de refuerzo como GANs (Redes Generativas Antagónicas), que utilizan modelos probabilísticos para la generación de patrones dinámicos. Integrar la teoría de secuencias en IA ha impulsado avances en numerosas áreas, desde chatbots hasta análisis predictivo.

referencia：

https://en.wikipedia.org/wiki/Sequence

https://en.wikipedia.org/wiki/Long_short-term_memory

https://en.wikipedia.org/wiki/Backtracking