¿Qué es un vector?

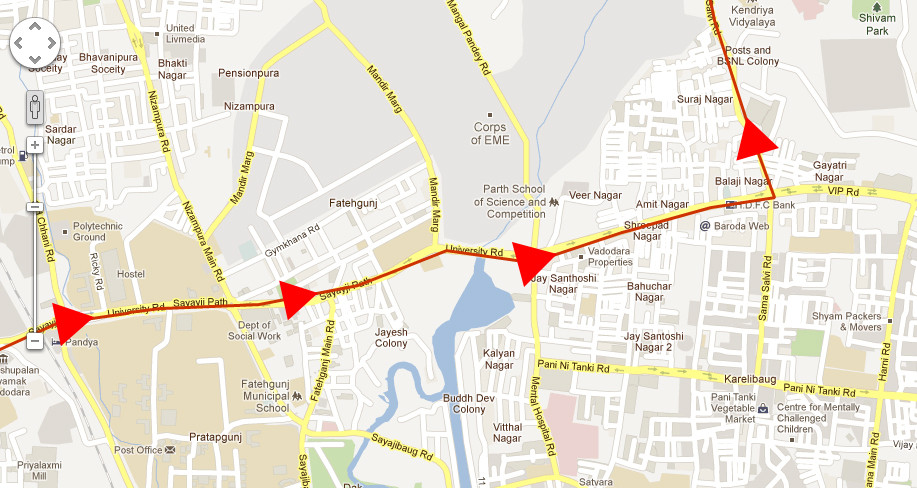
Los vectores, los objetos fundamentales utilizados en matemáticas para representar magnitud y dirección, cumplen la misma función en la vida real que nuestra brújula común: mostrarnos la dirección. Imagina pasear por un parque y de repente decidir dirigirte hacia un pequeño lago idílico, utilizando el mapa de tu smartphone como guía y la clara flecha que muestra como orientación - ¡tal es la vida involucrando vectores! Esta escena representa con precisión su papel, ya que los vectores están siempre presentes a lo largo de las experiencias cotidianas. Los vectores desempeñan una función integral en la ciencia, la ingeniería y la tecnología moderna: no solo representan tu dirección de viaje, sino que también miden la distancia a tu ubicación deseada. Este artículo introduce a los lectores desde la experiencia cotidiana en este emocionante ámbito detallando completamente sus conceptos básicos, métodos operativos y aplicaciones - ¡mucho más de lo que aparenta a simple vista!

Conceptos Básicos de Vectores

Definición y Representación  

Definición Matemática y Notación  

Las matemáticas definen un vector como cualquier cantidad con magnitud y dirección; esta entidad matemática representa posiciones espaciales o cantidades físicas con precisión. Los vectores se pueden denotar usualmente con símbolos como $\vec{v}=(v_1,v_2,\dots ,v_n)$, donde cada componente $v_i$ representa un valor a lo largo del respectivo eje de coordenadas - esto formaliza las operaciones y muestra claramente cada proyección a lo largo de cada eje de coordenadas; más manipulaciones algebraicas se construyen sobre esta base de conocimiento de vectores a medida que la formalización continúa progresivamente con el tiempo - proporcionando un conocimiento fundamental que refina y profundiza aún más la teoría sobre los vectores como entidades teóricas que abarcan espacios/bases/dimensiones, lo que hace que la comprensión de su teoría sea aún más profunda.

Intuición Geométrica  

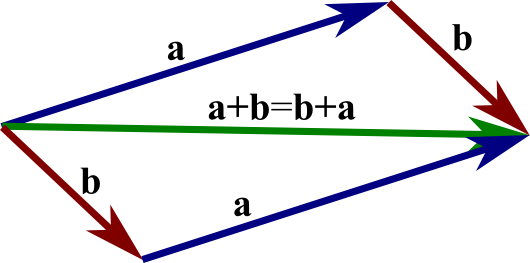
Geométricamente hablando, los vectores se pueden definir como un segmento de línea con flecha que comienza en un punto y lleva a otro punto, su longitud indica magnitud mientras la dirección muestra hacia dónde apunta. Un vector actúa como una flecha en un mapa que ayuda a las personas a navegar con precisión hacia sus metas ofreciendo una guía precisa para encontrar sus caminos. A través de la intuición geométrica, muchos conceptos algebraicos abstractos se vuelven concretos, haciendo que la suma de vectores, la resta y los cambios de dirección sean más accesibles, mientras que las representaciones gráficas hacen que sus ángulos y relaciones sean instantáneamente aparentes.

Propiedades Básicas  

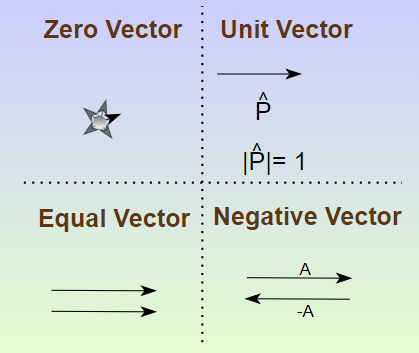
Vector Cero y Vector Unitario  

Los vectores cero $\vec{0}$ no tienen dirección y sirven como un elemento identidad al sumar vectores, mientras que los vectores unitarios con magnitud de uno suelen representar unidades estándar en direcciones específicas - por ejemplo, en sistemas de coordenadas bidimensionales $\vec{i}=(1,0)$ y $\vec{j}=(0,1)$ representan direcciones horizontal y vertical respectivamente; su introducción no solo simplifica la representación sino que también facilita la extracción y estandarización en problemas prácticos.

Vectores Paralelos, Perpendiculares y Otras Relaciones Fundamentales  

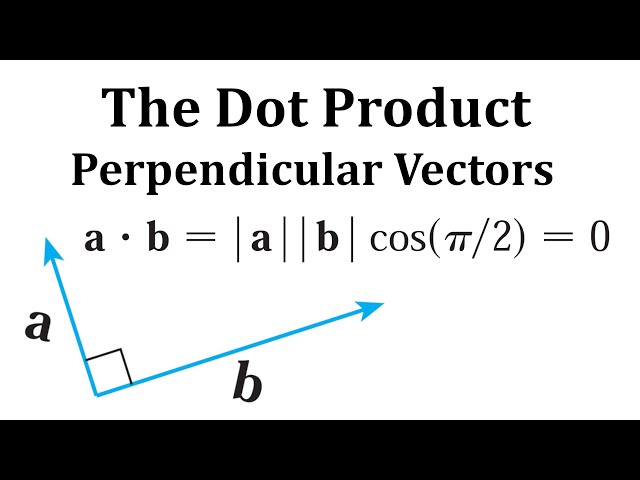
Los vectores paralelos comparten direcciones iguales u opuestas; cuando dos vectores perpendiculares se encuentran en ángulos rectos entre sí, se los llama ortogonales; para distinguir estas condiciones en dos vectores ortogonales, la siguiente condición se aplica a ambos $\vec{u}$ y $\vec{v}$ la condición.  

$\vec{u}\cdot \vec{v}=0$  

Esta propiedad de los espacios vectoriales es ampliamente utilizada en la práctica para establecer relaciones direccionales y realizar transformaciones de coordenadas, proporciona una base efectiva para discutir las bases y los esquemas de ortogonalización y es un elemento indispensable del análisis de espacios vectoriales.

Magnitud y Dirección  

Fórmulas y Métodos para el Cálculo  

La magnitud, también conocida como su tamaño o valor absoluto, de un vector, es su medida cuantitativa. Por ejemplo, para el vector bidimensional $\vec{v}=(v_1,v_2)$, su magnitud se puede encontrar como $\Vert \vec{v}\Vert =\sqrt{v_1^2+v_2^2},$

y para un vector tridimensional $\vec{u}=(u_1,u_2,u_3)$ es  

$\Vert \vec{u}\Vert =\sqrt{u_1^2+u_2^2+u_3^2}.$  

La determinación de dirección involucra descripciones tanto de magnitud como de ángulo de los vectores. Al tratar con vectores bidimensionales, el ángulo $\theta$ entre ellos y el eje horizontal se puede calcular usando la función arctángente, $\theta =\arctan \frac{v_2}{v_1}$. Una forma intuitiva pero precisa de representar cantidades físicas como fuerza o velocidad hace que la teoría de vectores sea aplicable en muchos campos de estudio.

Operaciones Vectoriales

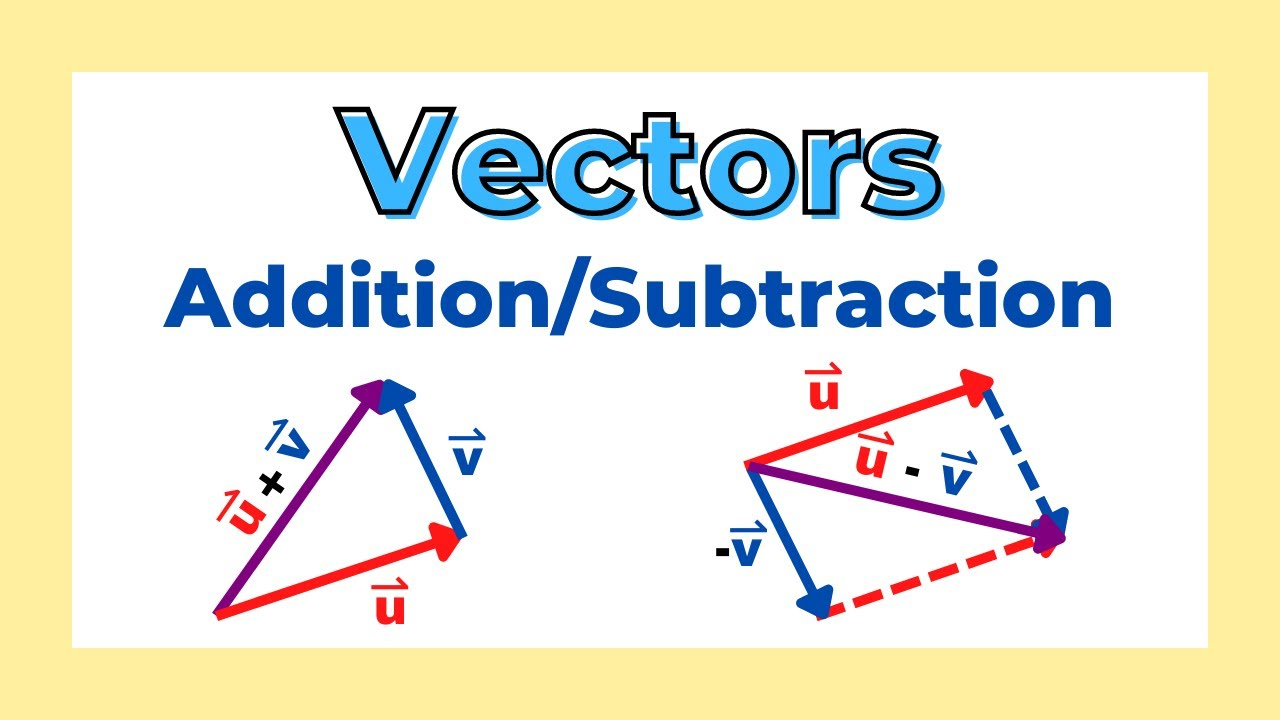
Adición y Sustracción

Leyes Operativas (Conmutatividad y Asociatividad)

La suma de vectores es una de las operaciones principales en álgebra lineal, proporcionando reglas confiables para sumar vectores. Según su ley conmutativa, cada vez que combinamos los vectores $\vec{u}$ y $\vec{v}$, obtenemos el resultado:

$\vec{u}+\vec{v}=\vec{v}+\vec{u}$.

De manera similar, la ley asociativa, expresada como

$(\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w})$,

indica que la agrupación no altera los resultados. La sustracción sigue con una resta consistente $\vec{u}-\vec{v}=\vec{u}+(-\vec{v})$

Esta propiedad verificada desempeña un papel integral en cálculos científicos simplificando problemas complejos asociados con ingeniería, gráficos por ordenador o física mediante la manipulación de vectores predecible y estandarizada de manera eficiente.

Ejemplos Típicos

Considera dos vectores bidimensionales$\vec{a}=(3,4)$ y $\vec{b}=(1,2)$ que se suman de la siguiente manera; su suma se puede expresar como $\vec{a}+\vec{b}=(3+1,4+2)=(4,6),$  

mientras que su diferencia se obtiene de $\vec{a}-\vec{b}=(3-1,4-2)=(2,2).$  

Estos ejemplos básicos ilustran claramente operaciones por componentes para la adición y sustracción.

Multiplicación Escalar

Reglas de Cálculo y Ejemplos de Aplicación

La multiplicación escalar se refiere a multiplicar un vector por un número real entero, cambiando efectivamente tanto su longitud como su dirección (si es negativo, la invierte). Dado un vector$\vec{v}=(v_1,v_2,\dots ,v_n)$ y una entrada de escalar $k$ , obtenemos $k\vec{v}=(k{v}_1,k{v}_2,\dots ,k{v}_n).$

Por ejemplo, asumiendo $k=2$ y configurando $\vec{v}=(3,4)$ resulta en $2\vec{v}=(6,8),$ con su dirección sin cambios. Esta operación duplica la longitud del vector manteniendo su dirección sin modificar.

Operaciones de Multiplicación

Producto Punto (Producto Escalar) Fórmula y Ejemplos

El producto punto (también referido como producto escalar) es una operación invaluable que convierte dos vectores en un valor escalar. Su fórmula se lee como:

$\vec{u}\cdot \vec{v}={\sum }_{i=1}^n{u}_i{v}_i$,

por ejemplo, si dos vectores tienen componentes $\vec{u}=(1,2)$ y $\vec{v}=(3,4)$ entonces el producto punto se calcula como $\vec{u}\cdot \vec{v}=1\cdot 3+2\cdot 4=3+8=11$.

El producto punto desempeña un papel esencial al establecer si dos vectores son ortogonales al igualar a cero, calcular proyecciones vectoriales y medir el ángulo entre vectores. Debido a estas propiedades, encuentra amplia aplicación en campos como la física, ingeniería y gráficos por computadora, demostrando así su significativa utilidad práctica.

Producto Cruz (Producto Vectorial) Fórmula y Ejemplos

Los productos cruz se aplican principalmente a vectores tridimensionales y proporcionan un nuevo vector que es perpendicular a ambos originales. Pueden describirse mediante esta ecuación de matriz:

$$\vec{u}\times \vec{v}=\left|\begin{array}{ccc}\vec{i}& \vec{j}& \vec{k}\\ u_1& u_2& u_3\\ v_1& v_2& v_3\end{array}\right|.$$  

Asumiendo $\vec{u}=(1,0,0)$ y $\vec{v}=(0,1,0)$, entonces su producto cruz sería $\vec{u}\times \vec{v}=(0,0,1),$ ; mostrando que su vector resultante está perpendicular al plano XY. Los productos cruz se emplean frecuentemente en ciencias físicas para describir torques y campos magnéticos.

Descomposición Vectorial

Extracción de Componentes Horizontales y Verticales

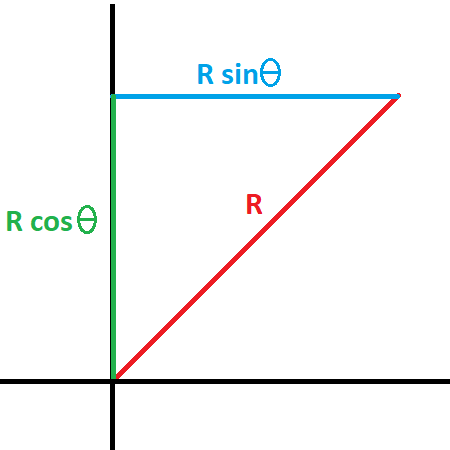
La descomposición vectorial involucra descomponer un vector en componentes mutuamente perpendiculares. Un vector bidimensional $\vec{v}$ puede descomponerse en componentes horizontales y verticales usando funciones seno y coseno:

$v_x=\Vert \vec{v}\Vert \cos \theta ,v_y=\Vert \vec{v}\Vert \sin \theta ,$  

donde $\theta$ es el ángulo entre el vector y el eje horizontal. En física, esta ecuación se puede utilizar para identificar componentes de movimiento.

Representación de Componentes en Múltiples Dimensiones

La descomposición vectorial sigue siendo efectiva incluso en espacios de mayores dimensiones al usar bases ortogonales como vectores base; cada vector puede entonces ser representado como la combinación lineal de esos vectores base; por ejemplo:

$\vec{v}=v_1{\vec{e}}_1+v_2{\vec{e}}_2+\cdots +v_n{\vec{e}}_n.$  

Esta forma de descomposición ayuda a simplificar el proceso de resolver problemas multidimensionales y se utiliza ampliamente en aplicaciones de análisis de datos y gráficos por computadora.

Vectores Avanzados y Extendidos

Vectores Espaciales y de Alta Dimensión  

Los vectores bidimensionales proporcionan la base para resolver problemas de mayor dimensión. Los vectores tridimensionales juegan un papel integral en el diseño de ingeniería, gráficos por computadora y control de movimiento robótico, ya que describen la posición, velocidad y fuerzas de los objetos en el espacio. Los vectores de alta dimensión tienen un papel igualmente fundamental en el análisis de grandes volúmenes de datos como herramientas para construir características de muestra y analizar correlaciones, como representar imágenes, audio o datos textuales como vectores de alta dimensión puede facilitar el modelado matemático de fenómenos complejos y el cálculo subsiguiente.

Ejemplos de Cálculo para Vectores Tridimensionales y de Ultra Alta Dimensión  

Tomando un vector tridimensional $\vec{v}=(v_1,v_2,v_3)$ como ejemplo, su magnitud se da por  

$\Vert \vec{v}\Vert =\sqrt{v_1^2+v_2^2+v_3^2}.$  

Para un vector de mayor dimensión $\vec{u}=(u_1,u_2,\dots ,u_n)$, la fórmula de magnitud se generaliza a  

$\Vert \vec{u}\Vert =\sqrt{{\sum }_{i=1}^n{u}_i^2}.$  

Considere, por ejemplo, un vector de cuatro dimensiones: $\vec{w}=(1,2,2,1)$; su magnitud se puede calcular usando esta ecuación:

$\Vert \vec{w}\Vert =\sqrt{1^2+2^2+2^2+1^2}=\sqrt{1+4+4+1}=\sqrt{10}.$

Escenarios de Aplicación Práctica y Significado Físico  

Los vectores tridimensionales proporcionan una herramienta intuitiva para la composición y descomposición de fuerzas que actúan sobre objetos, sus trayectorias y estados de rotación, proporcionando un medio efectivo para su composición o descomposición. Los ingenieros suelen emplear métodos vectoriales en análisis de estrés y vibración, mientras que los vectores de ultra alta dimensión sobresalen en ciencia de datos, análisis estadístico y aplicaciones de aprendizaje automático al medir distancias y ángulos entre vectores para cumplir con diversos objetivos de clasificación de datos, agrupación o eliminación de grupos. Estos usos prácticos de vectores profundizan aún más nuestra comprensión de los fenómenos físicos al tiempo que impulsan el desarrollo de teorías adicionales y metodologías computacionales relacionadas.

La Historia del Desarrollo y las Fronteras Teóricas de los Vectores

Antecedentes Históricos y Evolución Teórica

Los Orígenes del Concepto de Vector en el Desarrollo de las Matemáticas

La historia de los vectores se remonta a la antigua Grecia, donde los estudiosos de la geometría discutieron por primera vez sobre segmentos de línea dirigidos. En los siglos XVII y XVIII, con el establecimiento del Sistema de Coordenadas Cartesianas, los matemáticos combinaron gradualmente la intuición geométrica con operaciones algebraicas en la teoría de vectores, que ahora sustenta el desarrollo de la física moderna. En ese momento, los vectores se convirtieron no solo en herramientas esenciales para describir posiciones y movimientos de objetos, sino que también proporcionaron un respaldo matemático riguroso para desarrollos posteriores dentro de ella.

Principales Avances Teóricos y su Importancia

Con el desarrollo de teorías como los álgebras de Lie y el espacio euclidiano a mediados del siglo XIX, los vectores se ampliaron de manera sistemática. Los matemáticos introdujeron estructuras fundamentales como los espacios vectoriales y los espacios de producto interno. Un producto interno se define como $⟨\vec{u},\vec{v}⟩={\sum }_{i=1}^n{u}_i{v}_i.$   

Formulaciones como la teoría de vectores proporcionaron una base teórica sólida para muchos campos de las matemáticas y la física moderna, incluyendo métodos de ortogonalización como el proceso de Gram-Schmidt para ortogonalizar conjuntos de datos, así como la optimización y la mecánica cuántica. Con sus contribuciones innovadoras en la teoría de vectores, brindando un fuerte apoyo teórico a muchas ramas de las matemáticas y la física modernas.

El Impacto de las Teorías Matemáticas Emergentes en la Extensión de los Vectores

Las últimas décadas han presenciado avances significativos en topología, análisis funcional y geometría no euclidiana que han abierto nuevas vías para la exploración de vectores. Campos emergentes como el análisis de datos de alta dimensión, la teoría de variedades y los espacios tensoriales incorporan conceptos de vectores extendidos que los hacen más adecuados para resolver problemas estructurales no lineales que nunca antes. El aprendizaje automático utiliza vectores de características y métodos kernel, que utilizan vectores y sus estructuras de producto interno como medios para la proyección de datos y la reducción de dimensión, impulsando el desarrollo de la inteligencia artificial. A medida que surgen nuevas teorías que utilizan estos conceptos para este propósito, su importancia aumenta, ofreciendo al mismo tiempo ideas y métodos innovadores para aplicaciones multidisciplinarias.

Aplicaciones de Ingeniería y Física de Vectores

Análisis de Casos en Mecánica y Movimiento  

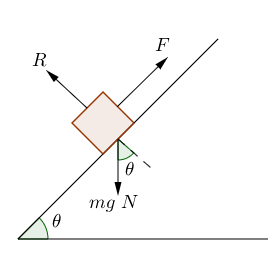
Los vectores en mecánica se utilizan para describir el movimiento y las fuerzas que actúan sobre los objetos, así como los cambios en la velocidad. Por ejemplo, los estudios de objetos que se mueven a lo largo de un plano inclinado muestran que su vector gravitacional puede descomponerse en componentes paralelos y perpendiculares: por ejemplo, su componente paralelo con el plano sería

$mg\sin \theta ,$  

mientras que el componente perpendicular es  

$mg\cos \theta .$  

Cálculos como estos ayudan a los ingenieros a medir tanto el estado de movimiento como la magnitud de la fricción con mayor precisión, presentando la velocidad y la aceleración como vectores para mostrar dirección y tasa de movimiento de manera más efectiva, permitiendo a los ingenieros diseñar sistemas de movimiento y dispositivos de seguridad más precisos.

Otros Ejemplos de Aplicación en los Campos de Matemáticas e Ingeniería  

Los vectores juegan un papel esencial en la mecánica física, así como en el análisis de circuitos, la ingeniería estructural y los gráficos por computadora. Las transformaciones vectoriales juegan un papel esencial en los gráficos por computadora al rotar y trasladar objetos 3D; la descomposición ortogonal de espacios vectoriales (como la transformada de Fourier) ayuda a reducir el ruido y extraer información de características; los problemas de programación lineal y optimización también dependen de operaciones vectoriales, ya que los espacios vectoriales restringidos proporcionan herramientas poderosas para resolver problemas de ingeniería complejos.

La Aplicación de Vectores en la Tecnología Moderna  

Con el progreso tecnológico continuo, los vectores han surgido como poderosas herramientas en el aprendizaje automático, la inteligencia artificial y el análisis de grandes datos. A través de métodos de incrustación, los textos e imágenes pueden transformarse en vectores de alta dimensión, permitiendo la extracción de características y el análisis de conglomerados. Además, las matrices de pesos de redes neuronales contienen numerosos vectores que componen matrices de pesos mientras que usando operaciones de producto interno de vectores, las correlaciones pueden calcularse eficientemente; todo esto ilustra la enorme vitalidad y potencial ilimitado de la teoría de vectores en la tecnología moderna.

A partir de un ejemplo de guía de dirección en el mundo real, este artículo examina los conceptos de vectores y reglas operativas mientras muestra sus amplias aplicaciones a espacios de alta dimensión, ingeniería mecánica y tecnología moderna. Desde sus humildes orígenes como simples flechas, han crecido hasta convertirse en herramientas sofisticadas que representan la belleza matemática mientras estimulan la innovación científica y fomentan avances interdisciplinarios, allanando el camino para el futuro brillo científico y posibilidades infinitas.

referencia:

https://en.wikipedia.org/wiki/Vector_(mathematics_and_physics)

https://en.wikipedia.org/wiki/Cross_product

https://en.wikipedia.org/wiki/Dot_product