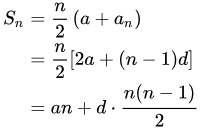¿Qué es una secuencia aritmética?

Las matemáticas pueden parecer abstractas, sin embargo, sus aplicaciones en nuestra vida diaria son profundas. Pensemos en instalar un suelo de madera y necesitar que cada tabla esté espaciada uniformemente como un ejemplo de algo conocido en matemáticas como una "sucesión aritmética," donde la diferencia entre términos consecutivos permanece constante a lo largo del tiempo. Este artículo ofrecerá un examen extenso de su definición, propiedades y aplicaciones prácticas; ¡haciendo que un concepto matemático de otra manera abstracto se vuelva accesible y tangible!

Representación y Conceptos Básicos de Secuencias Aritméticas

Para comprender completamente una secuencia aritmética, primero debemos entender su representación y conceptos básicos. Una secuencia aritmética es una serie en la que la diferencia entre términos consecutivos permanece constante. Esta simple regla le otorga a la secuencia su estructura y regularidad. Aquí, discutimos su definición, representación simbólica y componentes clave.

Definición

Una secuencia o progresión aritmética consiste en números en los cuales cualquier dos términos consecutivos siempre difieren en cantidades iguales; matemáticamente, esto puede escribirse como:

\(a_{n+1} - a_n = d\)  

En su esencia está lo que se conoce como la diferencia común\(d\), una constante fija que define la progresión dentro de cualquier secuencia. Por ejemplo, considere la secuencia \(2, 6, 10, 14, \dots\). Cada término aumenta en 4 unidades, lo que hace de esta una secuencia aritmética.

Representación Simbólica

Las secuencias aritméticas pueden expresarse típicamente usando la notación \(a_1, a_2, a_3, \dots, a_n\), donde \(a_1\) representa el primer término y los términos subsiguientes pueden representarse usando sus posiciones relativas dentro de la secuencia.

Primer Término (\(a_1\))  

Las secuencias aritméticas a menudo comienzan en su primer término \(a_1\). Por ejemplo, en la secuencia \(3, 6, 9, 12, \dots\), el primer término \(a_1 = 3\).

Diferencia Común (\(d\))  

La diferencia común es una cantidad fija que debe ser añadida (o restada) entre cualquier par de términos consecutivos en una secuencia que aumenta, disminuye o permanece constante. Determina si ocurre un crecimiento a lo largo de esta dirección o permanece estancada con el tiempo.

- Si \(d > 0\), la secuencia es creciente (por ejemplo, \(2, 4, 6, \dots\)).  

- Si \(d < 0\), la secuencia es decreciente (por ejemplo, \(10, 7, 4, \dots\)).  

- Si \(d = 0\), todos los términos son iguales (por ejemplo, \(5, 5, 5, \dots\)).

El \(n\)-ésimo Término (\(a_n\))  

El \(n\)-ésimo término de una secuencia aritmética puede calcularse basado en tres criterios: su posición \(n\), el primer término \(a_1\), y la diferencia común \(d\). Abordaremos cómo calcular \(a_n\) más adelante.

Fórmula General de Secuencias Aritméticas

Una secuencia aritmética deriva su poder de su relación recursiva y fórmula general. Una secuencia aritmética puede expresarse utilizando su forma general:

\(a_n = a_1 + (n-1)d\)  

Esta fórmula general hace posible calcular cualquier término en cualquier secuencia sin necesidad de calcular todos los anteriores primero. Por ejemplo, si asumimos dos términos anteriores con valores respectivos de \(a_1 = 2\) y \(d = 3\), respectivamente. Cuando esta ecuación se aplica a los \(5\)-ésimos términos se calcula como:

\(a_5 = 2 + (5-1) \cdot 3 = 2 + 12 = 14\)  

La fórmula general proporciona un medio efectivo para comprender y manipular secuencias aritméticas; exploraremos más a fondo en secciones posteriores.

Tipos de Secuencias Aritméticas

Las secuencias aritméticas vienen en muchas formas; entender sus diversas variedades nos ayuda a apreciar mejor su potencial completo. Las secuencias pueden clasificarse según el número de términos representados o métodos representados empleados, así como características de uso; en esta sección nos enfocamos en secuencias finitas e infinitas formadas de manera recursiva y explícita.

Secuencias Aritméticas Finitas

Las secuencias aritméticas finitas consisten en términos limitados que tienen claros puntos de inicio y fin, donde su número total \(n\), es conocido y preestablecido; un ejemplo sería \(3, 6, 9, 12, 15\), que es una secuencia finita que contiene cinco términos.

Las secuencias aritméticas finitas pueden ser herramientas muy útiles en la programación de eventos, planificación de pagos y organización de recursos. Por ejemplo, al entrenar flexiones durante 10 días consecutivos con 5 cada vez añadiendo 2 extra, la secuencia de entrenamiento se convertiría en \(5, 7, 9, \dots, 23\)con 10 términos dentro de ella y permite cálculos precisos como el conteo total de flexiones.

Secuencias Aritméticas Infinitas

Una secuencia aritmética infinita no termina y se extiende indefinidamente - un ejemplo sería \(1, 4, 7, 10, \dots\). Aquí los términos continúan aumentando sin límite.

Las secuencias infinitas son frecuentemente empleadas en matemáticas teóricas para propósitos como estudiar límites, crear patrones numéricos o explorar series. Una secuencia infinita de números impares como \(1, 3, 5, 7, \dots\). Aunque las secuencias infinitas tienden a tener aplicaciones prácticas menos comunes que las finitas, proporcionan la base de muchos modelos y sistemas matemáticos.

Formas Recursivas vs. Explícitas

Forma Recursiva  

Las formas recursivas de una secuencia aritmética definen cada término según lo que ocurrió antes. Una fórmula podría verse así:

\(a_{n+1} = a_n + d,\quad n \geq 1\)  

este enfoque funciona particularmente bien al producir secuencias iterativamente usando algoritmos de computadora.

Forma Explícita  

La forma explícita proporciona una fórmula directa para calcular cualquier término directamente sin referencia a los anteriores, representada por:

\(a_n = a_1 + (n-1)d\)  

Por ejemplo, si \(a_1 = 3\) y \(d = 2\), el \(10\)-ésimo término es:  

\(a_{10} = 3 + (10-1) \cdot 2 = 21\)  

Esta forma proporciona cálculos rápidos y eficientes al trabajar con grandes secuencias o términos específicos.

Al clasificar las secuencias aritméticas en formas finitas e infinitas y distinguir entre sus representaciones recursivas y explícitas, destacamos su versatilidad y amplia aplicabilidad. Estas distinciones nos servirán para prepararnos para nuestra posterior exploración en fórmulas esenciales para crear estas secuencias.

Fórmulas de Secuencias Aritméticas

Las fórmulas son herramientas poderosas para entender y manipular secuencias aritméticas, proporcionándonos un medio eficiente para calcular términos específicos, sumar totales eficientemente, identificar problemas relacionados con secuencias afines y más. En esta sección veremos tres fórmulas esenciales: estas son: la fórmula del \(n\)-ésimo término, las fórmulas recursivas y las fórmulas para la suma junto con sus derivaciones y aplicaciones.

 \(n\)-ésimo Término Fórmula

La fórmula del \(n\)-ésimo término es el núcleo de las secuencias aritméticas. Calcula el valor de cualquier término \(a_n\) en función de su posición \(n\), el primer término \(a_1\), y la diferencia común \(d\):  

\(a_n = a_1 + (n-1)d\)  

La derivación es simple: empezando desde \(a_1\), cada término subsiguiente se puede representar de la siguiente manera: el segundo término es \(a_2 = a_1 + d\), el tercer término es \(a_3 = a_1 + 2d\), y así sucesivamente. En general, el \(n\)-ésimo término se representa como el primer término más \((n-1)\) múltiplos de la diferencia común.

Considere, por ejemplo, una secuencia con una condición inicial de \(a_1 = 5\) y \(d = 3\). Para calcular su décimo término directamente en esta fórmula:

\(a_{10} = 5 + (10-1) \cdot 3 = 5 + 27 = 32\)  

Esta fórmula encuentra eficientemente cualquier término en una secuencia ascendente sin necesidad de considerar todos los anteriores primero.

Fórmula Recursiva

Las fórmulas recursivas se utilizan para representar una secuencia aritmética en términos de su relación entre términos sucesivos:

\(a_{n+1} = a_n + d,\quad n \geq 1\)  

Esta representación requiere el conocimiento del término inicial \(a_1\) para generar la secuencia. Por ejemplo, si \(a_1 = 2\) y \(d = 4\):  

\(a_2 = a_1 + d = 6,\quad a_3 = a_2 + d = 10,\quad a_4 = a_3 + d = 14\)  

Las fórmulas recursivas pueden ser ideales para cálculos iterativos en programación; sin embargo, son menos convenientes para identificar términos distantes en comparación con la fórmula explícita del \(n\)-ésimo término.

Fórmula para la Suma de la Secuencia Aritmética

La fórmula para la suma calcula la suma de los primeros \(n\) términos de una secuencia aritmética, conocida como\(S_n\):

\(S_n = \frac{n}{2} \cdot (a_1 + a_n)\)  

Si el \(n\)-ésimo término \(a_n\) es desconocido, sustituya \(a_n = a_1 + (n-1)d\) en la fórmula para obtener:  

\(S_n = \frac{n}{2} \cdot [2a_1 + (n-1)d]\)  

Esta fórmula facilita la suma de manera simple y eficiente. Por ejemplo, en una secuencia donde \(a_1 = 2\), \(d = 5\), y \(n = 4\), la suma es:  

\(S_4 = \frac{4}{2} \cdot [2 \cdot 2 + (4-1) \cdot 5] = 2 \cdot [4 + 15] = 38\)  

Derivación de la Fórmula de la Suma

Se puede crear una fórmula para la suma emparejando términos de los extremos opuestos de una secuencia aritmética juntos. Para una secuencia aritmética \(a_1, a_2, \dots, a_n\), escríbala tanto hacia adelante como hacia atrás:  

\(S_n = a_1 + a_2 + \dots + a_n\)  

\(S_n = a_n + a_{n-1} + \dots + a_1\)  

Sumando estos da:  

\(2S_n = n \cdot (a_1 + a_n)\)  

Resolviendo para \(S_n\) se obtiene:  

\(S_n = \frac{n}{2} \cdot (a_1 + a_n)\)  

Cuando un factor desconocido \(a_n\) es desconocido, al reemplazarlo por \(a_n+1\) se crea la forma generalizada \(a_1 + (n-1)d\) .

Estas fórmulas nos permiten trabajar eficientemente con secuencias aritméticas, proporcionando cálculos rápidos incluso para escenarios grandes o complejos. En la siguiente sección, demostraremos operaciones específicas utilizando estas fórmulas a través de ejemplos prácticos.

Cálculos y Operaciones con Secuencias Aritméticas

Las secuencias aritméticas desempeñan un papel esencial tanto en la resolución de problemas matemáticos como en escenarios prácticos, requiriendo varios cálculos y operaciones. Ya sea para continuar una secuencia existente, encontrar términos faltantes o deducir incógnitas a partir de fuentes de información incompletas basadas en conocimiento parcial, las secuencias aritméticas proporcionan bloques fundamentales de construcción matemática que requieren un uso competente; esta sección explora técnicas clave para realizarlas eficazmente.

Cómo Calcular una Secuencia Aritmética

Para identificar o continuar una secuencia aritmética, el primer paso debe ser localizar su primer término (\(a_1\)) y la diferencia común (\(d\)). Conociendo estos detalles, cualquier término de la secuencia se puede calcular utilizando su fórmula para el \(n\)-ésimo término:  

\(a_n = a_1 + (n-1)d\)  

Considere, por ejemplo, una secuencia en la que \(a_1 = 5\) y \(d = 3\). Calcular sus primeros términos da:

\(a_1 = 5, \quad a_2 = 5 + 3 = 8, \quad a_3 = 5 + 6 = 11, \quad a_4 = 5 + 9 = 14\)  

Si necesitamos encontrar el término vigésimo, sustituyendo en la fórmula:  

\(a_{20} = 5 + (20-1) \cdot 3 = 5 + 57 = 62\)  

Este método asegura que incluso los términos distantes en una secuencia se puedan identificar sin sumar \(d\) manualmente de forma repetida.

Además, aquí hay una calculadora AI que puede calcular la secuencia fácil y rápidamente!

Cómo Encontrar Términos Faltantes

Los problemas del mundo real a veces implican términos faltantes en una secuencia aritmética; al estudiar sus relaciones entre términos, estos pueden ser reconstruidos. Por ejemplo, dada una secuencia con \(a_1 = 2\), \(a_4 = 14\), y una \(d\) desconocida, podemos resolver \(d\) sustituyendo los valores conocidos en la fórmula del \(n\)-ésimo término:  

\(a_4 = a_1 + 3d \quad \text{entonces} \quad 14 = 2 + 3d\)  

Resolviendo, obtenemos \(d = 4\). Una vez determinada la diferencia común, los términos faltantes se pueden encontrar:  

\(a_2 = a_1 + d = 2 + 4 = 6, \quad a_3 = a_2 + d = 6 + 4 = 10\)  

Así, la secuencia completa es \(2, 6, 10, 14, \dots\).

Encontrar el Último Término a partir de la Suma de la Secuencia

Si se da la suma de los primeros \(n\) términos (\(S_n\)), pero el último término (\(a_n\)) es desconocido, podemos usar la fórmula de la suma y resolver algebraicamente para \(a_n\):  

\(S_n = \frac{n}{2} \cdot (a_1 + a_n) \quad \Rightarrow \quad a_n = \frac{2S_n}{n} - a_1\)  

Por ejemplo, suponga \(a_1 = 3\), \(n = 5\), y \(S_5 = 40\). El último término se calcula como:  

\(a_5 = \frac{2 \cdot 40}{5} - 3 = 16 - 3 = 13\)  

Este enfoque muestra cómo los datos parciales de la secuencia pueden ayudar a descubrir información crítica faltante.

Estas técnicas de expansión de secuencias, reconstrucción de términos faltantes y resolución de incógnitas son componentes integrales para entender las secuencias aritméticas. Desde las matemáticas teóricas hasta las aplicaciones prácticas, estas habilidades permiten un manejo claro y eficiente de los problemas relacionados con secuencias. A continuación, examinaremos las representaciones gráficas de las secuencias para comprender mejor sus características lineales.

Representación Gráfica de Secuencias Aritméticas

Las secuencias aritméticas pueden representarse gráficamente no solo a través de números y fórmulas, sino también con representaciones geométricas, proporcionándonos una mayor comprensión de su estructura y propiedades. Al trazar sus términos, obtenemos una visión más clara de su relación directa con las funciones lineales, así como una mejor comprensión de sus características.

Secuencias Lineales y su Significado Geométrico

Cuando se trazan como puntos en un plano de coordenadas cartesianas, los términos de una secuencia aritmética como \(a_1, a_2, a_3, \dots, a_n\)forman una línea recta. Cuando se aplica esta fórmula: \(a_n = a_1 + (n-1)d\):

1. La coordenada horizontal \(x\)representa la ubicación del término en la posición \(n\).

2. La coordenada vertical \(y\)representa su valor \(a_n\).

Considere, por ejemplo, la secuencia \(2, 5, 8, 11, \dots\), donde \(a_1 = 2\) y \(d = 3\). trazada sobre una línea recta como se muestra aquí. La representación de cada término da como resultado los puntos \((1, 2), (2, 5), (3, 8), (4, 11)\) en esta línea recta que reflejan una tasa de cambio constante (3 siendo la diferencia común en la secuencia). Esta linealidad refleja la tasa de cambio constante (la diferencia común \(d = 3\)) dentro de la secuencia.

Secuencias Aritméticas y Funciones Lineales

La naturaleza de línea recta de una secuencia aritmética proviene de su conexión con funciones lineales; por ejemplo, la fórmula para cualquier término dado de una secuencia aritmética puede escribirse como una ecuación lineal:

\(a_n = dn + (a_1 - d)\) 

En cada punto a lo largo de la cronología de esta secuencia, \(d\) sirve como su pendiente - reflejando la tasa de cambio de sus términos - mientras que su intercepto se define por \((a_1 - d)\). Cuando\(d > 0\), su línea se inclina hacia arriba, significando una secuencia ascendente. Por el contrario, cuando \(d < 0\), desciende, indicando una secuencia decreciente; cuando \(d\) es igual a cero, significa que sus puntos se encuentran en una misma línea horizontal, ya que todos los términos de su historia tienen tasas de cambio iguales a lo largo del tiempo.

Aplicaciones Prácticas de Secuencias Aritméticas

Las secuencias aritméticas son herramientas poderosas utilizadas en múltiples campos que van desde la economía hasta la arquitectura. Sus estructuras simples pero flexibles permiten modelar patrones, diseñar sistemas y resolver problemas del mundo real de manera efectiva, como se ilustra aquí con respecto al crecimiento económico y los diseños estéticos arquitectónicos. Exploramos dos áreas donde estas secuencias juegan un papel integral: la expansión económica y los diseños estéticos en arquitectura.

Crecimiento Económico y Cálculo de Salarios

La economía y las finanzas a menudo emplean procesos lineales que pueden ser representados con precisión mediante un modelo de secuencia aritmética, como el ajuste salarial. Un ejemplo común sería la acumulación de salarios: cuando los empleados comienzan a recibir un pago salarial inicial así como incrementos anuales con el tiempo, esto crea una secuencia aritmética en términos de salarios a lo largo de los años.

Por ejemplo, si el salario inicial de un empleado es \(5000\) y el aumento anual es \(200\), la progresión salarial se convierte en \(5000, 5200, 5400, \dots\). Usando la fórmula del término \(n\)-ésimo, podemos predecir el salario en el quinto año:

\(a_5 = a_1 + (n-1)d = 5000 + (5-1) \cdot 200 = 5800 \ \text{unidades}\)

Además, para calcular el salario total recibido en cinco años, usamos la fórmula de la suma:

\(S_5 = \frac{n}{2} \cdot (a_1 + a_5) = \frac{5}{2} \cdot (5000 + 5800) = 27,000 \ \text{unidades}\)

Esta metodología se extiende más allá de los salarios para rastrear el crecimiento o disminución de ingresos o gastos anuales, utilizando tendencias consistentes como ingresos o gastos anuales, donde ocurren aumentos o disminuciones consistentes. Industrias experimentando una expansión constante con producción fija cada año pueden usar secuencias aritméticas para predecir su rendimiento en los años siguientes: por ejemplo, si el volumen de producción aumenta en \(10,000\) unidades cada año, entonces la producción acumulada para ciertos años puede calcularse fácilmente utilizando este enfoque.

Secuencias Aritméticas en Diseño Arquitectónico

Los elementos arquitectónicos a menudo aprovechan la armonía estética inherente a las secuencias matemáticas para agregar belleza y función. Desde escaleras hasta diseños de asientos escalonados, su uniformidad y proporcionalidad aportan tanto funcionalidad como belleza al juego.

Diseño de Escaleras

Imagina que tenemos una escalera donde el primer escalón mide \(15\ cm\) de alto, aumentando \(2\ cm\) en cada escalón. Esto forma una secuencia aritmética: \(15, 17, 19, \dots\). Para determinar la altura del décimo escalón, aplicamos la fórmula del término \(n\)-ésimo:

\(h_{10} = h_1 + (n-1)d = 15 + (10-1) \cdot 2 = 15 + 18 = 33 \ \text{cm}\)

Estos diseños reflexivos ofrecen a los usuarios comodidad mientras mantienen la seguridad estructural, haciendo que las secuencias aritméticas sean cruciales para la exactitud y precisión en la construcción.

Estructuras Escalonadas

Los diseños de asientos escalonados en teatros, estadios deportivos y espacios públicos que aumentan de altura o ancho consistentemente siguen una secuencia aritmética, que a menudo se crea usando diseños escalonados que aumentan la profundidad o altura de cada fila consistentemente usando una secuencia aritmética. Por ejemplo, cada fila sucesiva del teatro puede comenzar a \(100\ cm\) de profundidad antes de aumentar \(10\ cm\) cada fila. Al hacer los cálculos necesarios para la construcción usando fórmulas de suma, se vuelve fácil calcular la profundidad para el cálculo de la profundidad de la vigésima fila, así como el material total requerido utilizando fórmulas de suma: ¡creando estructuras que son tanto atractivas visualmente como seguras estructuralmente! ¡Una secuencia aritmética asegura que estas estructuras permanezcan tanto visualmente atractivas como estructuralmente seguras! Su naturaleza secuencial asegura esto.

Estos ejemplos demuestran cómo las secuencias aritméticas puentean las matemáticas con la vida real; desde modelar el crecimiento económico hasta diseñar arquitectura y diseños funcionales pero atractivos, estos ejemplos muestran cómo las herramientas matemáticas versátiles pueden aplicarse a través de disciplinas, así como en la vida cotidiana.

Las secuencias aritméticas son maravillas matemáticas: ¡simples pero estructuradas y poderosas a la vez! En este artículo, desglosamos sus conceptos básicos: desde la magia del primer término hasta la diferencia común; exploramos fórmulas esenciales como la fórmula del término \(n\)-ésimo o fórmula de suma; se proporcionaron métodos para descubrir términos faltantes o expandir secuencias fácilmente así como visualizar representaciones de líneas rectas para ilustrar que estos simples patrones podrían abrir puertas de oportunidades infinitas. ¡Lleno de teoría, trucos de fórmulas y ejemplos del mundo real, este artículo mostró cómo los simples patrones podrían abrir puertas de oportunidades infinitas!

referencias：

https://en.wikipedia.org/wiki/Arithmetic_progression

https://en.wikipedia.org/wiki/Recursion

https://en.wikipedia.org/wiki/Summation