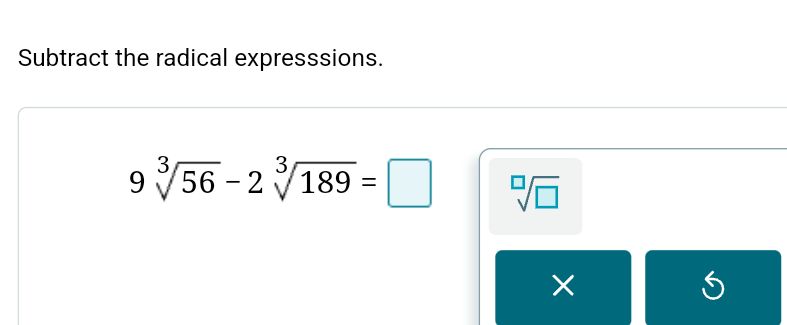
Subtract the radical expresssions. $$ 9 \sqrt[3]{56}-2 \sqrt[3]{189}= $$ $$ \square $$

Question

UpStudy AI · Accepted Answer

To subtract the radical expressions $$ 9 \sqrt[3]{56} - 2 \sqrt[3]{189} $$, we first simplify each cube root.

1. **Simplifying $$ \sqrt[3]{56} $$**:
   $$
   56 = 2^3 \cdot 7
   $$
   Therefore,
   $$
   \sqrt[3]{56} = \sqrt[3]{2^3 \cdot 7} = \sqrt[3]{2^3} \cdot \sqrt[3]{7} = 2 \sqrt[3]{7}
   $$

2. **Simplifying $$ \sqrt[3]{189} $$**:
   $$
   189 = 3^3 \cdot 7
   $$
   Therefore,
   $$
   \sqrt[3]{189} = \sqrt[3]{3^3 \cdot 7} = \sqrt[3]{3^3} \cdot \sqrt[3]{7} = 3 \sqrt[3]{7}
   $$

Now we can substitute these simplifications back into the original expression:
$$
9 \sqrt[3]{56} - 2 \sqrt[3]{189} = 9(2 \sqrt[3]{7}) - 2(3 \sqrt[3]{7})
$$

Calculating each term:
$$
9(2 \sqrt[3]{7}) = 18 \sqrt[3]{7}
$$
$$
2(3 \sqrt[3]{7}) = 6 \sqrt[3]{7}
$$

Now we can combine these results:
$$
18 \sqrt[3]{7} - 6 \sqrt[3]{7} = (18 - 6) \sqrt[3]{7} = 12 \sqrt[3]{7}
$$

Thus, the final result is:
$$
\boxed{12 \sqrt[3]{7}}
$$$$ 12 \sqrt[3]{7} $$

Subtract the radical expresssions. \[ 9 \sqrt[3]{56}-2 \sqrt[3]{189}= \] \( \square \)

Solución de inteligencia artificial de Upstudy

Responder

Solución

Bonus Knowledge

preguntas relacionadas

Latest Algebra Questions