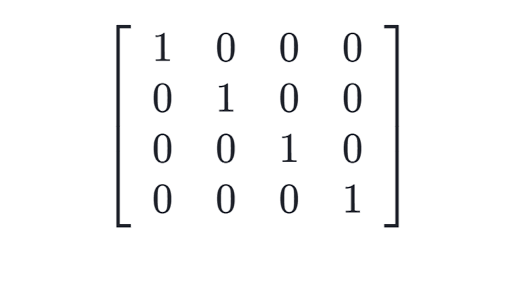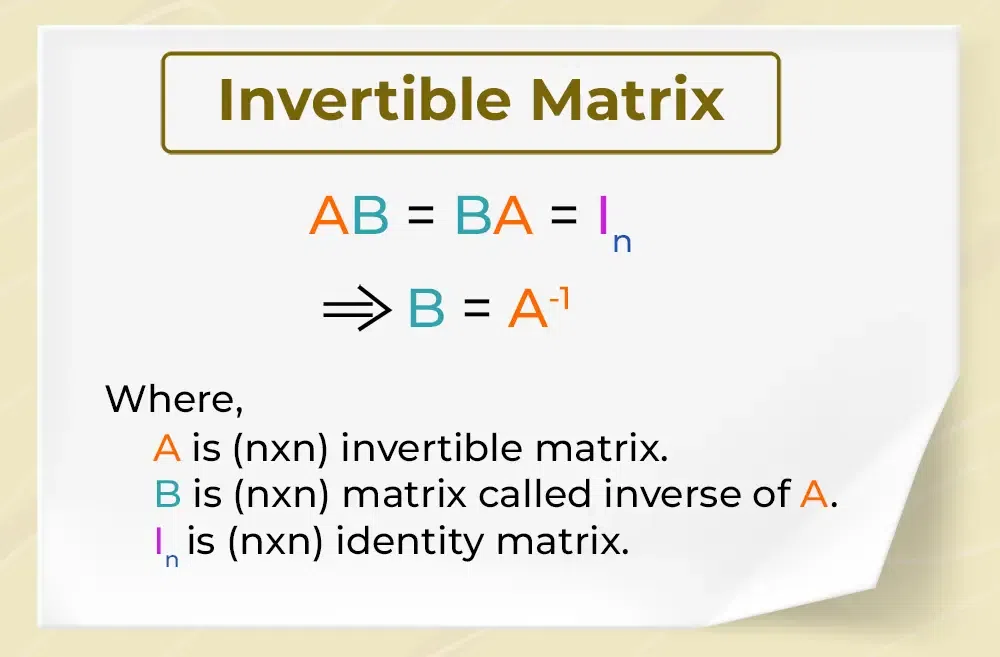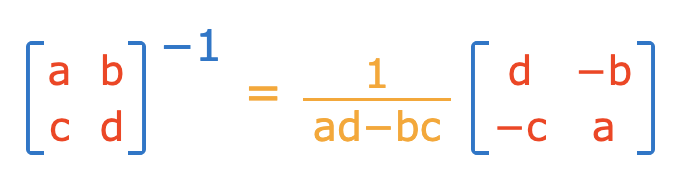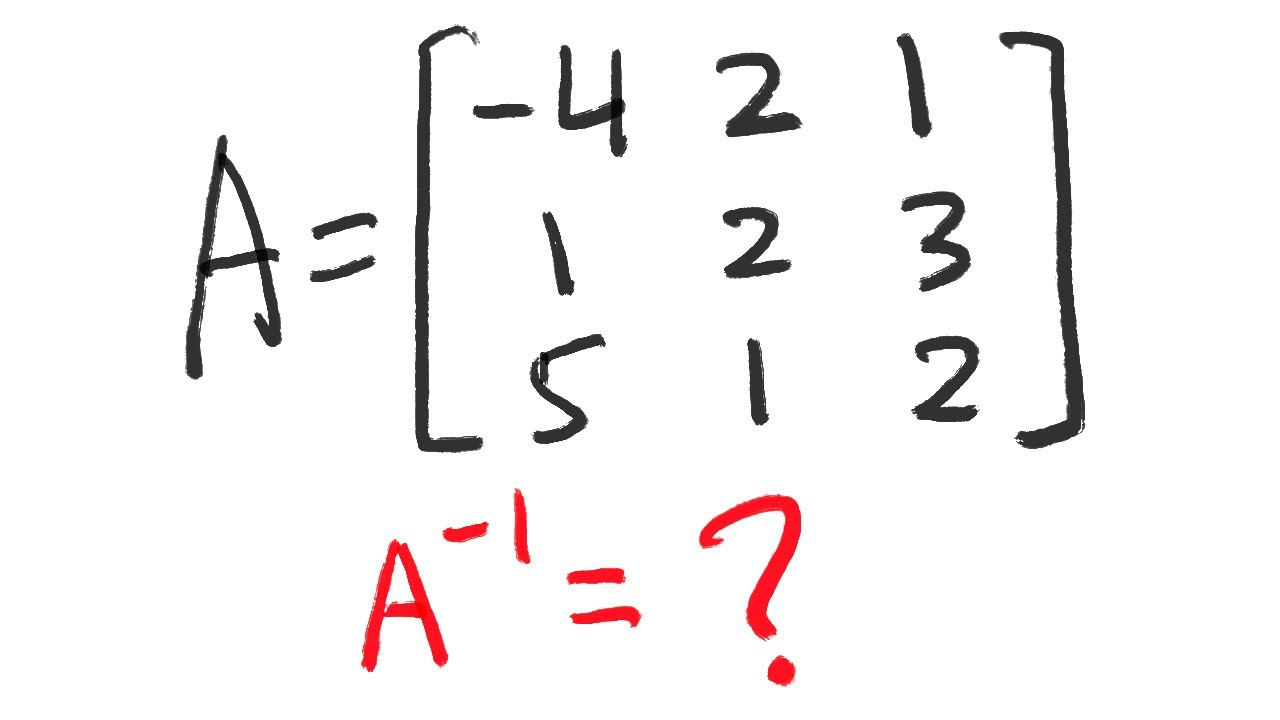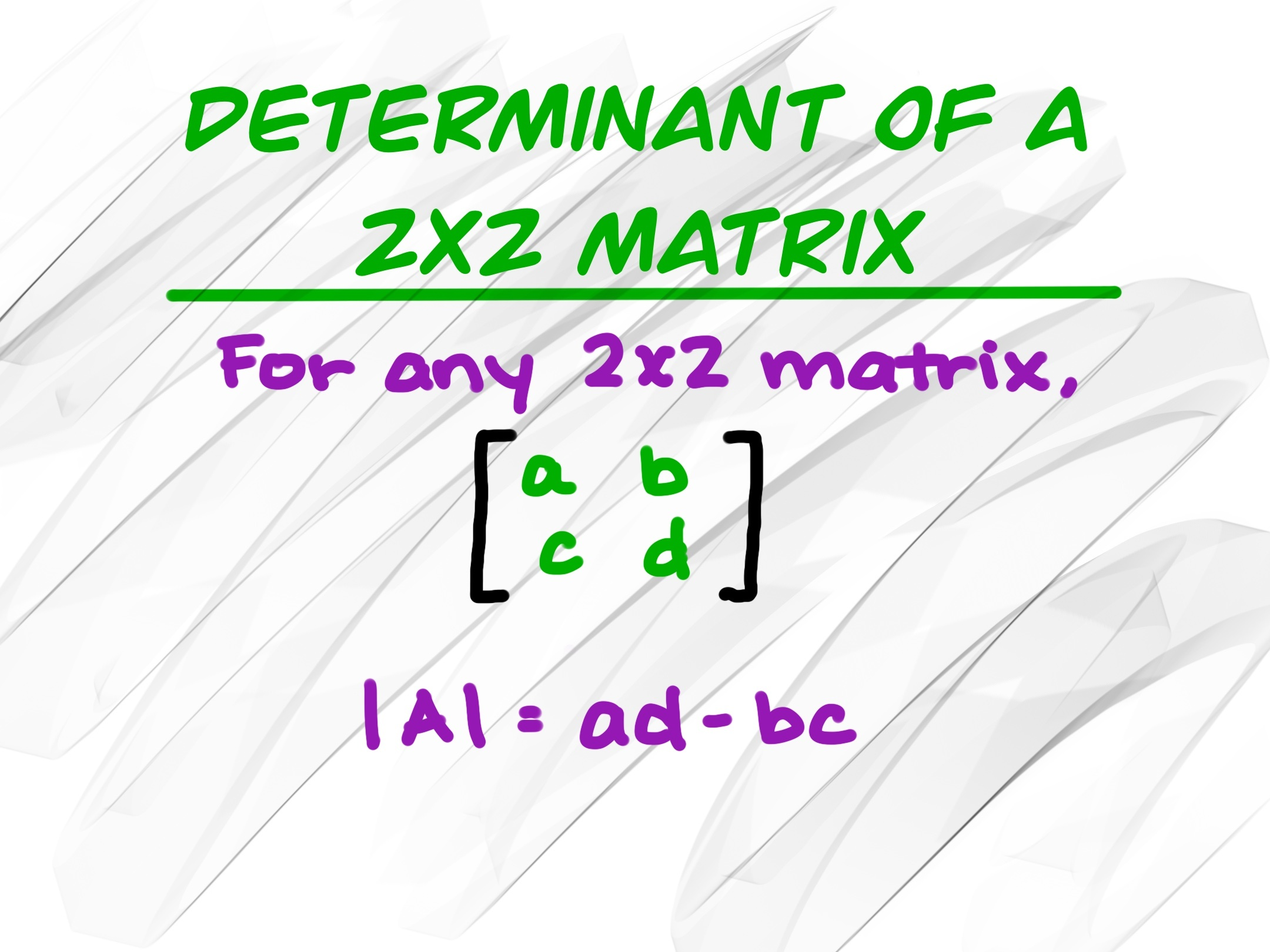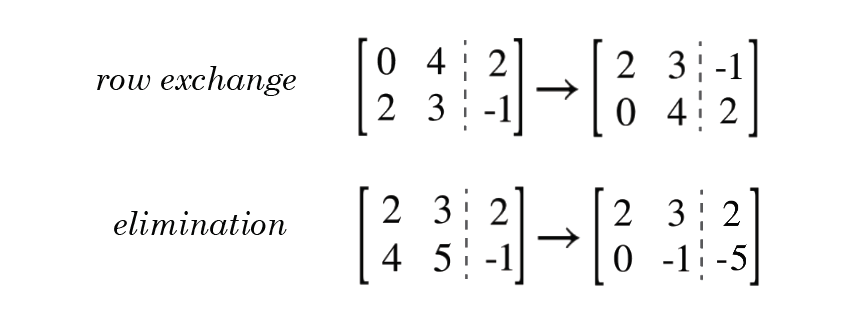¿Cómo Calcular la Inversa de una Matriz?

¿Qué es la Inversa de una Matriz?

Definición y Concepto

La inversa de una matriz es un concepto que se aplica a matrices cuadradas (matrices donde el número de filas es igual al número de columnas). La inversa de una matriz cuadrada \(A\) se denota como \(A^{-1}\). Si tal matriz existe, satisface la siguiente propiedad:

\(A \cdot A^{-1} = A^{-1} \cdot A = I\)

Donde \(I\) es la matriz identidad, una matriz cuadrada que consiste en unos en su diagonal y ceros en todas las otras entradas. Una matriz que posee una inversa se denomina matriz invertible o no singular. Las matrices sin inversa se denominan matrices singulares.

Por ejemplo, considere una simple matriz \(2×2\) \(A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}\). Si \(A^{-1}\) existe, entonces multiplicar \(A\) por su inversa dará la matriz identidad \(2×2\) \(I = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\).

Matriz Identidad y Condiciones para Inversas

La matriz identidad \(I\) es el elemento fundamental de la inversión de matrices. Cumple la misma función para la multiplicación de matrices que el número \(1\) cumple en la multiplicación escalar. Para la matriz \(A\), multiplicar por \(I\) no cambia \(A\):

\(A \cdot I = I \cdot A = A\)

Tres condiciones esenciales deben cumplirse para que exista la inversa de una matriz:

1. La matriz debe ser cuadrada: Solo matrices cuadradas (por ejemplo, \(2×2\), \(3×3\) o \(n×n\)) son elegibles para inversión. Las matrices no cuadradas, como \(2×3\), no pueden tener una inversa.

2.Una matriz debe tener un determinante distinto de cero: esta medida cuantifica propiedades escalares dentro de su estructura de matriz cuadrada. Una matriz con propiedades de determinante cero o negativo se considera singular y no posee una representación de matriz inversa.

3. Las matrices deben poseer rango completo: Esto significa que todas las filas (o columnas, en términos de matrices) de un arreglo deben ser linealmente independientes entre sí.

Métodos Comunes para Calcular la Inversa de una Matriz

Existen múltiples métodos para calcular la inversa de una matriz cuadrada, pero la elección del método a menudo depende del tamaño de la matriz y su estructura. Aquí nos enfocamos en procedimientos paso a paso para \(2×2\) y \(3×3\) matrices y discutimos enfoques generales para matrices más grandes.

Truco para Matrices \(2×2\)

Encontrar la inversa de una matriz \(2×2\) es típicamente sencillo. Dada una matriz \(A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}\), su inversa \(A^{-1}\) existe solo si el determinante es diferente de cero. El determinante (\(\text{det}(A)\)) se calcula como:

\(\text{det}(A) = ad - bc\)

La fórmula para la inversa de una matriz \(2×2\) es:

\(A^{-1} = \frac{1}{\text{det}(A)} \begin{bmatrix} d & -b \\ -c & a \end{bmatrix}\)

Si \(\text{det}(A) = 0\), la matriz no tiene inversa.

Fórmula y Explicación

Utilizando esta fórmula, podemos invertir matrices \(2×2\) simples con facilidad. Por ejemplo, sea \(A = \begin{bmatrix} 2 & 1 \\ 5 & 3 \end{bmatrix}\).

1. Calcula el determinante:

\(\text{det}(A) = (2)(3) - (5)(1) = 6 - 5 = 1\)

2. Sustituye en la fórmula:

\(A^{-1} = \frac{1}{1} \begin{bmatrix} 3 & -1 \\ -5 & 2 \end{bmatrix} = \begin{bmatrix} 3 & -1 \\ -5 & 2 \end{bmatrix}\)

Uso en el Mundo Real

La fórmula de inversión para matrices \(2×2\) es ampliamente usada en sistemas pequeños como sistemas mecánicos básicos, ingeniería eléctrica para cálculos de impedancia y modelos económicos.

Inversa de Matrices \(3×3\)

El proceso para invertir una matriz \(3×3\) es más complejo y consiste en cuatro pasos principales.

Paso 1: Calcular el Determinante

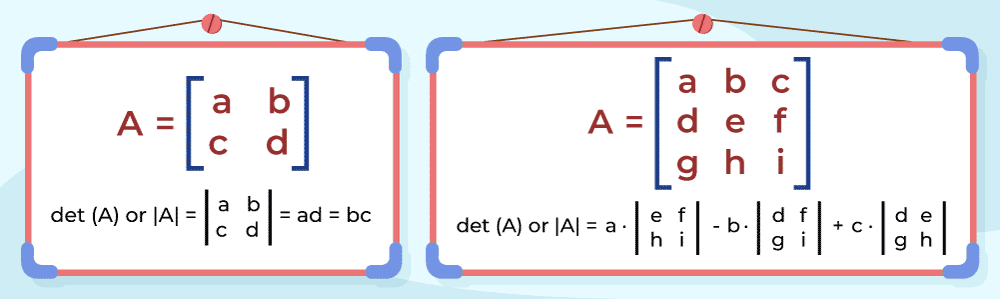
Dada una matriz \(3×3\) \(A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}\), el determinante se calcula usando:

\(\text{det}(A) = a(ei − fh) − b(di − fg) + c(dh − eg)\)

Si \(\text{det}(A) = 0\), la matriz no puede ser invertida.

Paso 2: Calcular Menores y Cofactores

Para cada elemento \(a_{ij}\) de la matriz, calcula su menor eliminando la \(i\)-ésima fila y la \(j\)-ésima columna y calculando el determinante de la \(2×2\) matriz restante. El cofactor es el menor multiplicado por \((-1)^{i+j}\).

Por ejemplo, para \(A = \begin{bmatrix} 2 & 3 & 1 \\ 4 & 1 & 5 \\ 7 & 6 & 8 \end{bmatrix}\), el cofactor de \(a_{11}\) (2) es:

\(\text{Cofactor}(a_{11}) = (-1)^{1+1} \cdot \text{det}\begin{bmatrix} 1 & 5 \\ 6 & 8 \end{bmatrix} = (8 − 30) = -22\)

Paso 3: Construir la Matriz Adjunta

La adjunta de \(A\) se construye reemplazando cada elemento de \(A\) con su cofactor y luego transponiendo la matriz resultante.

Paso 4: Usar la Fórmula

Finalmente, la inversa se calcula como:

\(A^{-1} = \frac{1}{\text{det}(A)} \cdot \text{Adj}(A)\)

Este enfoque paso a paso garantiza un cálculo preciso para matrices \(3×3\).

Operaciones Elementales de Fila y Columna

Las operaciones elementales de fila y columna ofrecen una solución eficiente para la inversión de matrices. Al adjuntar una matriz identidad al lado derecho de la matriz y realizar operaciones de reducción de filas, transformamos ambas versiones en identidades equivalentes mientras las convertimos ambas en versiones invertidas.

Pasos para Invertir una Matriz Usando Aumento

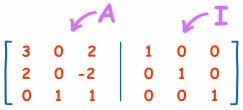
1. Formar una matriz aumentada: Para \(A\), adjunta la matriz identidad \(I\) para formar \([A | I]\).

2. Realizar reducción de filas: Usa la eliminación de Gauss o operaciones de fila para transformar \(A\) en \(I\). Aplica las mismas operaciones a \(I\) simultáneamente.

3. Leer el resultado: Una vez que \(A\) se convierte en \(I\), el \(I\) modificado a la derecha se convierte en \(A^{-1}\).

Este método es particularmente útil para matrices más grandes y puede implementarse fácilmente en herramientas computacionales.

Escenarios Donde Este Método Es Útil

Las operaciones de filas son especialmente útiles al tratar con solvers numéricos en programación de computadoras o cuando se requiere un proceso claro y sistemático para matrices más grandes.

Determinantes y su Papel en la Inversión de Matrices

Los determinantes proporcionan información esencial sobre las matrices cuadradas. Los determinantes juegan un papel crucial en decidir si una matriz puede ser invertida, ya que sus propiedades están directamente vinculadas a ello.

Importancia de los Determinantes

Los determinantes surgen naturalmente durante operaciones con matrices, tales como resolver sistemas de ecuaciones lineales, derivar autovalores y obtener inversas.

Cuando el determinante de una matriz cuadrada es igual a cero, su estado se denomina singularidad, lo que significa que no puede ser invertida en otra forma de matriz.

Para la intuición, considere la interpretación geométrica de los determinantes:

- En dos dimensiones (\(2×2\) matrices), el determinante corresponde al área del paralelogramo formado por los vectores columna de la matriz.

- En tres dimensiones (\(3×3\) matrices), el determinante indica el volumen del paralelepípedo definido por los vectores columna.

Cuando el determinante es igual a cero, los vectores son linealmente dependientes y colapsan en un espacio de menor dimensión (por ejemplo, una línea o un punto).

Esto explica por qué una matriz singular no tiene una inversa.

Matrices Singulares vs. No Singulares

Una matriz singular tiene un determinante cero y no tiene un equivalente invertible; por el contrario, las no singulares presentan determinantes distintos de cero, lo que permite su inversión. Comprender por qué ciertas matrices poseen o no inversa requiere entender esta distinción entre tipos de matrices singulares y no singulares.

Por ejemplo:

- La matriz \(B = \begin{bmatrix} 1 & 2 \\ 2 & 4 \end{bmatrix}\) es singular porque su determinante es:

\(\text{det}(B) = (1×4) - (2×2) = 4 - 4 = 0\)

Esto ocurre porque las filas (o columnas) de \(B\) son linealmente dependientes.

- La matriz \(C = \begin{bmatrix} 2 & 1 \\ 3 & 4 \end{bmatrix}\) es no singular porque su determinante es:

\(\text{det}(C) = (2×4) - (1×3) = 8 - 3 = 5\)

Propiedades Únicas de los Determinantes

Los determinantes pueden proporcionar varias propiedades útiles que simplifican los cálculos relacionados con matrices:

1. Efecto de Intercambio de Filas: Alterar dos filas (o columnas) puede cambiar su determinante. Este cambio afecta su signo y, por lo tanto, su cálculo.

2. Propiedades de Sumas/Resta de Filas: Simplemente sumar múltiplos de una fila en otra no altera su determinante.

3. Escalado: Multiplicar cualquier fila (o columna) por un entero escala su determinante por ese factor.

Utilizar estas propiedades hace que los cálculos manuales sean más rápidos.

Más allá de \(3×3\) Matrices: Técnicas Avanzadas

Para matrices mayores que \(3×3\), el esfuerzo computacional requerido para la inversión aumenta significativamente. Enfoques avanzados, como la eliminación Gaussiana y la explotación de estructuras de matrices especiales, se han vuelto cruciales.

Eliminación Gaussiana

La eliminación Gaussiana es una técnica sistemática para resolver sistemas de ecuaciones lineales que también se puede modificar para encontrar inversas de matrices. Los pasos son similares a los métodos de reducción por filas discutidos anteriormente:

1. Aumenta la matriz \(A\) con la matriz identidad \(I\).

2. Aplica técnicas de reducción por filas para transformar \(A\) en la matriz identidad.

3. La matriz identidad transformada se convierte en la inversa \(A^{-1}\).

Por ejemplo, considera una matriz de \(4×4\) \(D\). La eliminación gaussiana puede involucrar cientos de pasos cuando se realiza manualmente; sin embargo, con computadoras, se vuelve mucho más simple. La eliminación gaussiana ha demostrado ser un método computacional eficiente y escalable que es ideal para tareas computacionales.

Casos Especiales: Matrices Diagonales y Ortogonales

Ciertas categorías de matrices, incluidas las matrices diagonales y ortogonales, poseen propiedades especiales que facilitan la inversión.

Matrices Diagonales

Una matriz diagonal se refiere a una matriz cuadrada donde todos los elementos no diagonales son cero. Por ejemplo,

\(D = \begin{bmatrix} 3 & 0 & 0 \\ 0 & 7 & 0 \\ 0 & 0 & 5 \end{bmatrix}\)

La inversa de una matriz diagonal \((D)\) se calcula tomando el recíproco de sus elementos diagonales:

\(D^{-1} = \begin{bmatrix} 1/3 & 0 & 0 \\ 0 & 1/7 & 0 \\ 0 & 0 & 1/5 \end{bmatrix}\)

Matrices Ortogonales

Una matriz ortogonal \(Q\) es una matriz cuadrada cuyas filas y columnas son vectores ortonormales. Estas matrices satisfacen la propiedad:

\(Q^{-1} = Q^T\)

Esto hace que su inversión sea computacionalmente económica en comparación con matrices generales.

Enfoque Creativo: Visualizando Inversas de Matrices a través de la Teoría de Grafos

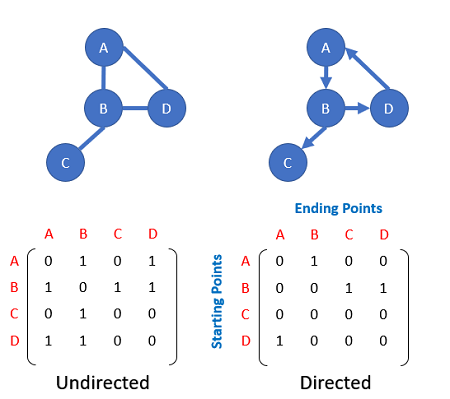
Las matrices a veces pueden ilustrarse y entenderse usando otras áreas de las matemáticas, como la teoría de grafos; este enfoque no tradicional proporciona una intuición útil para los principiantes.

Conectando Matrices y Grafos

Considere un grafo \(G\), donde la matriz de adyacencia \(A\) representa las conexiones entre nodos. La inversa de \(A\), cuando existe, puede verse como codificación de relaciones o dependencias indirectas entre los nodos en el grafo.

Por ejemplo, en un grafo de red social donde los nodos representan individuos y los bordes representan amistades, la matriz de adyacencia inversa podría representar relaciones de confianza indirectas entre personas.

Ejemplo Amigable para Principiantes de Teoría de Grafos

Imagine una pequeña red descrita por la \(2×2\) matriz \(A = \begin{bmatrix} 1 & 1 \\ 1 & 2 \end{bmatrix}\). Su inversa:

\(A^{-1} = \begin{bmatrix} 2 & -1 \\ -1 & 1 \end{bmatrix}\)

Tiene entradas que reflejan relaciones ponderadas entre los nodos, ajustadas por la estructura de la red. Aunque este es un concepto abstracto, relacionar las inversas de matrices con sistemas del mundo real como las redes puede ayudar a la comprensión.

Consejos y Trucos para Cálculos Más Rápidos

Acelerar las inversiones de matrices puede implicar entender atajos, además de aprovechar la tecnología. A continuación, compartimos algunos consejos prácticos.

Técnicas de Memorización para Matrices Pequeñas

Para \(2×2\) matrices, memorizar la fórmula para la inversión es suficiente. Para matrices ligeramente más grandes (\(3×3\) específicamente), practica calcular menores y cofactores para internalizar el proceso.

Verificación Rápida de Soluciones

Después de calcular la inversa, verifique su resultado multiplicando la matriz \(A\) por su inversa \(A^{-1}\). El producto debe dar la matriz identidad \(I\).

Por ejemplo:

\(A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad A^{-1} = \begin{bmatrix} -2 & 1 \\ 1.5 & -0.5 \end{bmatrix}\)

Verifique multiplicando:

\(A \cdot A^{-1} = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\)

Este paso evita propagar errores en cálculos posteriores.

Aplicaciones Reales de la Inversión de Matrices

La inversión de matrices tiene aplicaciones críticas en numerosos dominios. A continuación, describimos tres áreas clave donde desempeña un papel vital.

Ciencia – Resolución de Sistemas de Ecuaciones

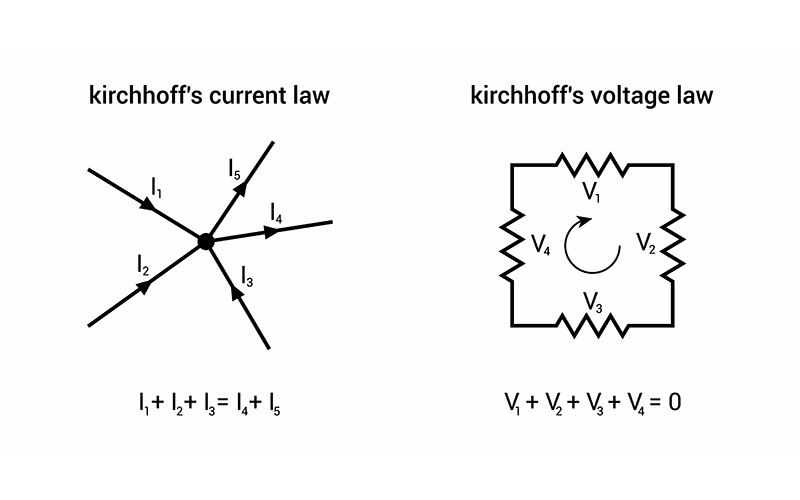
La inversión de matrices se emplea ampliamente en física y química para resolver sistemas de ecuaciones lineales, por ejemplo, en el análisis de circuitos eléctricos cuando las leyes de Kirchhoff crean ecuaciones en forma de matriz que deben resolverse utilizando formas de inversión de matrices; su uso permite calcular corrientes y voltajes no identificados con mayor precisión; de manera similar en mecánica cuántica, al resolver la ecuación de Schrödinger, generalmente se incluye el uso de inversión de matrices para predecir las funciones de onda de partículas así como sus distribuciones de probabilidad.

Ingeniería – Control y Estabilidad

La ingeniería utiliza la inversión de matrices como una técnica esencial tanto en teoría de control como en el análisis de sistemas mecánicos. La robótica se basa en esta práctica para resolver sus problemas de cinemática inversa utilizando la inversión de matrices; de manera similar, el análisis de vibraciones emplea la inversión de matrices de rigidez/masa para evaluar las respuestas del sistema a fuerzas dinámicas para una máxima eficiencia de diseño y estabilidad del sistema.

Estadística/Aprendizaje Automático – Optimización y Modelado

La estadística utiliza matrices de covarianza que han sido invertidas mediante el análisis discriminante gaussiano o cálculos de distancia de Mahalanobis para establecer relaciones entre variables, mientras que el aprendizaje automático se basa en la inversión para optimizar problemas como la refinación de pesos para regresiones o el entrenamiento de redes neuronales; la inversión de matrices acelera la convergencia hacia parámetros óptimos en espacios de alta dimensión.

Estas aplicaciones demuestran cómo la inversión de matrices puede ayudar a resolver problemas complejos en campos científicos, de ingeniería y computacionales.

Palabras Finales: Elegir el Método Correcto

La elección del método para invertir una matriz depende de su tamaño, estructura y contexto. Herramientas computacionales como MATLAB, la biblioteca NumPy de Python y Wolfram Mathematica pueden agilizar el proceso.

Resumen de Métodos Discutidos

Este artículo revisó métodos abreviados para \(2×2\) matrices, cálculos paso a paso para \(3×3\) matrices, herramientas computacionales para matrices más grandes y las propiedades únicas de matrices especiales.

Importancia del Entendimiento Fundamental

Aunque el software puede calcular rápidamente las inversiones de matrices, comprender el proceso matemático es clave para diagnosticar errores, optimizar el código y aplicar estos conceptos de manera efectiva.

Conclusión

La inversión de matrices es un tema indispensable que abarca matemáticas, ingeniería, física, ciencias de la computación y más allá. Calcular y entender matrices inversas es fundamental para resolver problemas del mundo real que van desde el análisis de circuitos eléctricos y la optimización del movimiento de robots en ingeniería hasta realizar análisis estadísticos que respaldan modelos de aprendizaje automático. Ya sea invirtiendo una simple \(2×2\) matriz o tratando con matrices a gran escala en cálculos avanzados, dominar estas técnicas proporciona herramientas invaluables para resolver problemas.

La inversión de matrices se destaca como un método excepcional para simplificar y proporcionar soluciones estructuradas a sistemas complejos de ecuaciones. No solo es útil en términos de conveniencia computacional, sino que comprender su teoría subyacente también profundiza nuestra comprensión de principios matemáticos clave como determinantes, independencia lineal y transformaciones de matrices, mejorando la precisión de las aplicaciones mientras ampliamos nuestra capacidad de innovar nuevas herramientas matemáticas que se adapten rápidamente para enfrentar nuevos desafíos.

El software ha hecho que invertir matrices sea más rápido y accesible; sin embargo, tener una sólida base teórica permite a los profesionales verificar resultados, solucionar errores y seleccionar métodos apropiados para problemas específicos de manera más rápida y confiada. El dominio de la inversión de matrices se convierte así no solo en una habilidad técnica sino en una oportunidad para mejorar las habilidades de pensamiento crítico así como el entendimiento matemático, que son habilidades importantes tanto en entornos académicos como profesionales.

Referencia:

https://mathresearch.utsa.edu/wiki/index.php?title=The_Geometric_Interpretation_of_the_Determinant

https://chem.libretexts.org/Courses/Grinnell_College/CHM_364%3A_Physical_Chemistry_2_(Grinnell_College)/03%3A_The_Schrodinger_Equation_and_a_Particle_in_a_Box/3.04%3A_Wavefunctions_Have_a_Probabilistic_Interpretation

https://www.neuralconcept.com/post/the-role-of-structural-dynamic-analysis-in-engineering-design