¿Cómo Calcular la Probabilidad?

¿Qué es la Probabilidad?

Definiendo la Probabilidad

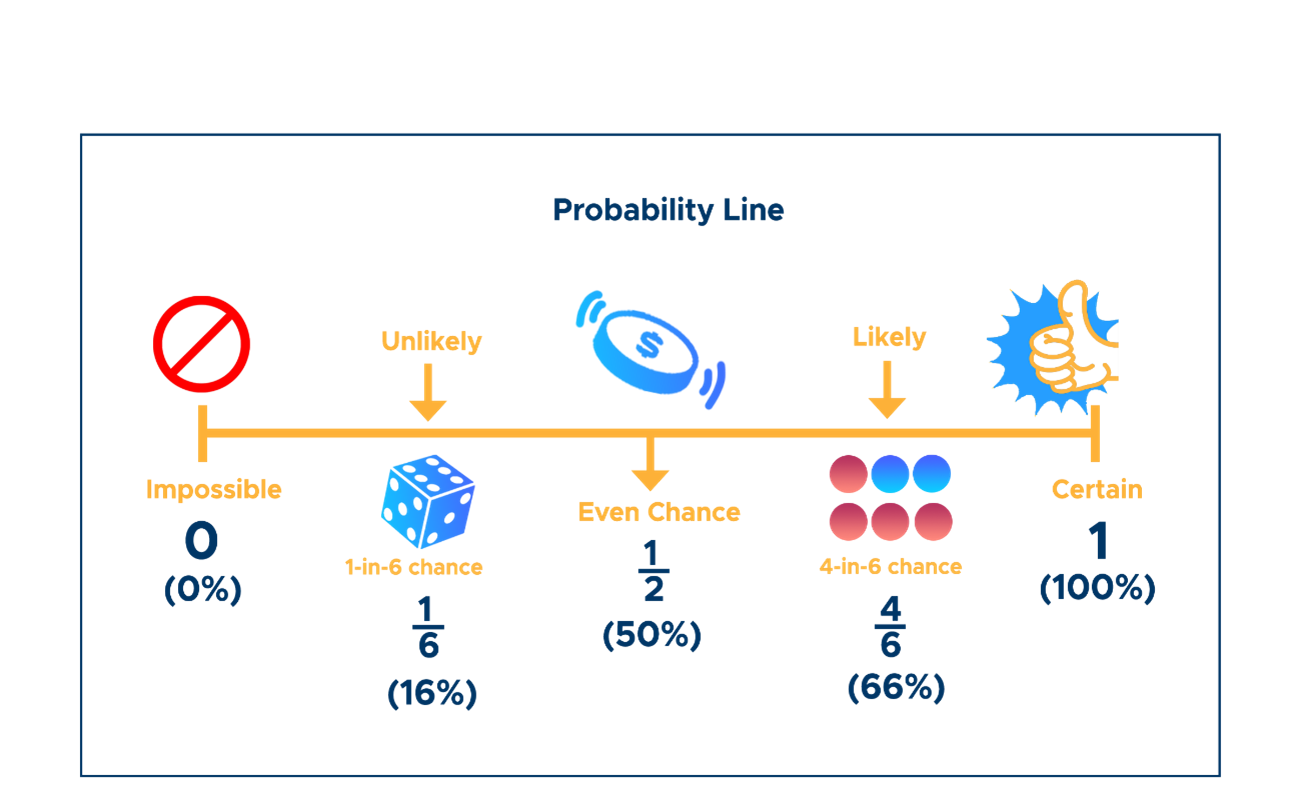
La probabilidad mide la posibilidad de que algo ocurra y se expresa como un número entre 0 y 1. 0 indica imposibilidad, mientras que uno significa certeza; lanzar una moneda justa da una probabilidad de caer en cara del 50%, por ejemplo.

La fórmula para calcular la probabilidad es simple:

P(Evento) = Resultados Favorables / Total de Resultados Posibles

Aquí, "resultados favorables" se refiere a los resultados que nos interesan, mientras que "total de resultados posibles" cuenta todos los resultados que podrían ocurrir.

Elementos Básicos de Probabilidad

Resultados

Estos representan todos los resultados potenciales de un experimento. Por ejemplo, cuando se lanza un dado estándar de seis caras, los resultados podrían ser 1, 2, 3, 4, 5, o 6.

Evento

Un subconjunto deseado de resultados. Por ejemplo, sacar un 5 en el dado constituye un evento.

Espacio Muestral

Todos los resultados son posibles en un experimento dado.

Tome una baraja de cartas, por ejemplo:

El espacio muestral incluye todas las 52 cartas.

El evento podría ser sacar un As, que ofrece resultados favorables de 4.

Por Qué Es Importante Entender la Probabilidad

Probabilidad se aplica mucho más allá de los lanzamientos de dados o juegos de cartas. Tiene muchas aplicaciones en múltiples áreas, incluyendo

Gestión de Riesgos - para calcular primas de seguros según la probabilidad de accidentes;

Medicina - diagnosticar enfermedades usando probabilidades predictivas de resultados de pruebas;

IA y Aprendizaje Automático: Estimando probabilidades con algoritmos predictivos.

El dominio de la probabilidad va mucho más allá de ejercicios teóricos: te equipa con habilidades para examinar situaciones críticamente y tomar decisiones informadas.

Calculando la Probabilidad de Eventos Simples

Calcular la probabilidad de eventos simples implica seguir un proceso simple de tres pasos.

Cálculo Paso a Paso

Paso 1: Definir el Evento

Identifica en qué resultado te estás concentrando. Por ejemplo, si estás lanzando un dado estándar y quieres conocer la probabilidad de sacar un 5, el evento es "sacar un 5."

Paso 2: Determinar los Resultados Posibles Totales

Observa el espacio de muestra del experimento. Con un lanzamiento de un dado de seis caras:

Los resultados posibles son 1, 2, 3, 4, 5, y 6.

Resultados totales = 6.

Paso 3: Aplicar la Fórmula de Probabilidad

Ahora calcula:

P(Sacar un 5)=Resultados Favorables/Resultados Posibles Totales=\(\frac{1}{6}​≈0.1667\)

Ejemplo:

Si deseas la probabilidad de obtener caras al lanzar una moneda, hay 1 resultado favorable (caras) de 2 posibles (caras y cruz). Por lo tanto:

P(Caras)=\(\frac{1}{2}​​=0.5\)

Errores Comunes a Evitar

Los principiantes a menudo cometen errores al identificar resultados favorables o totales:

Olvidar todos los resultados posibles: por ejemplo, en problemas de baraja de cartas, no considerar el palo como parte de un resultado.

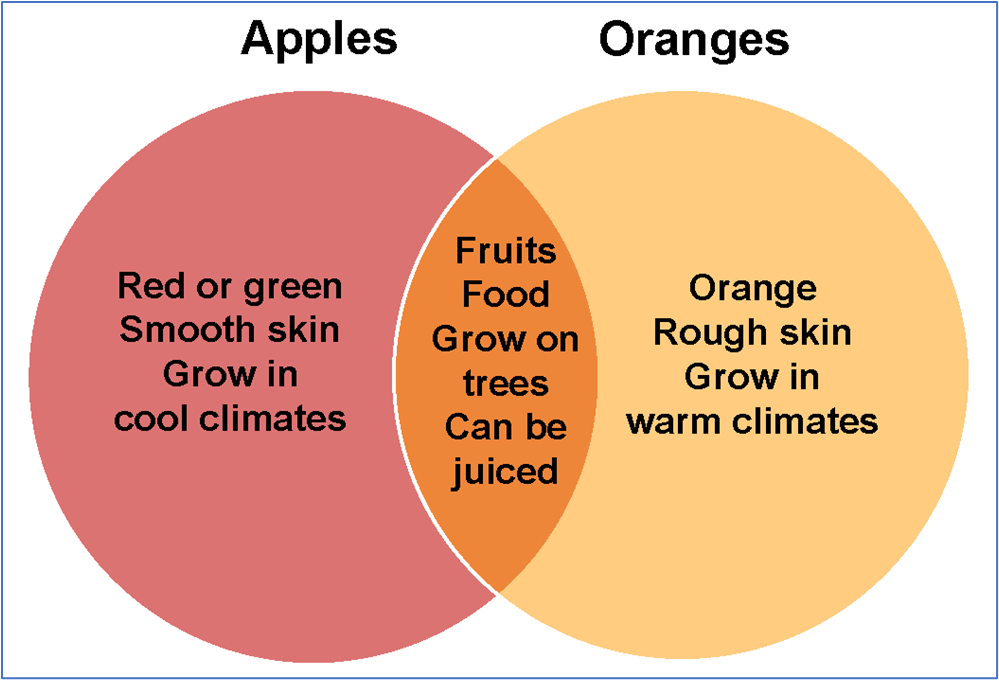
Asumir eventos mutuamente excluyentes cuando los resultados pueden superponerse: por ejemplo, al calcular probabilidades de Reinas rojas sin considerar superposiciones entre cartas rojas y Reinas, puede llevar a resultados confusos. Ayudas visuales como diagramas de Venn o tablas de probabilidad pueden ser soluciones efectivas para abordar estos problemas.

Visualizando Eventos Usando Diagramas

Para problemas de eventos simples, los diagramas pueden ayudar. Por ejemplo:

Ejemplo de Gráfico de Barras: Representa la frecuencia de cada lado de un dado en lanzamientos repetidos para afianzar la comprensión de probabilidades iguales.

Diagrama de Venn Simple: Si lanzas un dado para números mayores que 3, visualiza las superposiciones entre {4, 5, 6} y otros subconjuntos de eventos, si los hay.

Probabilidad para Múltiples Eventos

Los escenarios del mundo real a menudo implican múltiples eventos que ocurren juntos o en secuencia. Para tales casos, necesitas herramientas adicionales.

Eventos Independientes

Si el resultado de un evento no afecta al otro, son independientes.

Ejemplo: Lanzar un dado y tirar una moneda.

Fórmula:

P(A y B)=P(A)×P(B)

Escenario:

¿Cuál es la probabilidad de obtener cara y un 6?

P(Obtener cara) = 1/2

P(Obtener un 6) = 1/6

P(Cara y 6)=\(\frac{1}{2}​×\frac{1}{6}​=\frac{1}{12}\)

Eventos Dependientes

Con eventos dependientes, el resultado de uno afecta la probabilidad del otro.

Ejemplo: Robar cartas de una baraja sin devolverlas.

Fórmula:

P(A y B)=P(A)×P(B∣A)

Aquí, P(B|A) representa la probabilidad de B dado que A ha ocurrido.

Escenario:

La probabilidad de robar dos As seguidos de una baraja mezclada:

P(Robar el primer As) = 4/52

P(Robar el segundo As) = 3/51 (ya que un As ya ha sido retirado)

P(Dos Ases)=\(\frac{4}{52}​×\frac{3}{51}​=\frac{1}{221}\)

Eventos Combinados: Reglas de OR y AND

Eventos Mutuamente Excluyentes:

Si dos eventos no pueden ocurrir simultáneamente:

P(A o B)=P(A)+P(B)

Eventos No Mutuamente Excluyentes:

Si los eventos pueden superponerse:

P(A o B)=P(A)+P(B)−P(A y B)

Escenario:

En un mazo de cartas, ¿cuál es P(Robar un Rey o un Pica)?

P(Rey) = 4/52

P(Pica) = 13/52

P(Rey y Pica) = 1/52 (Rey de Picas)

P(Rey o Pica)=\(\frac{4}{52}​+\frac{13}{52}−\frac{1}{52}​=\frac{16}{52}​=\frac{4}{13}​\)

Árboles de Eventos para Múltiples Escenarios

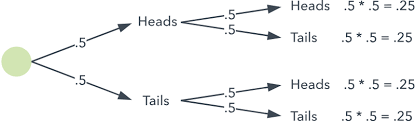
Para visualizar múltiples eventos, utiliza árboles de eventos, que representan escenarios desde una rama. Por ejemplo:

Camino 1 (Cara, Cara): P=0.5×0.5=0.25

Camino 2 (Cara, Cruz): P=0.5×0.5=0.25, y así sucesivamente.

Aplicaciones Reales de la Probabilidad

La probabilidad no es solo un concepto teórico confinado a los libros de texto o aulas. Juega un papel integral en diversas situaciones de la vida real, ayudando a tomar decisiones, predecir eventos futuros y gestionar riesgos.

Escenarios Cotidianos Donde la Probabilidad es Útil

Exploremos aplicaciones prácticas donde la probabilidad está en acción:

Predicción del Clima

Los meteorólogos utilizan la probabilidad para predecir el clima, como un "30% de probabilidad de lluvia." Este porcentaje se calcula usando datos históricos y modelos atmosféricos para ayudar a las personas a planificar su día.

Aplicaciones de Tráfico y Navegación

Google Maps y Waze emplean la teoría de la probabilidad para predecir congestiones; sus algoritmos estiman retrasos de tráfico basándose en millones de experiencias de usuarios.

Salud

Las pruebas médicas producen resultados probabilísticos. Por ejemplo, la sensibilidad de las pruebas PCR de COVID brinda información sobre la probabilidad de obtener un diagnóstico positivo verdadero dado un resultado positivo en la prueba.

Análisis Deportivo

Los análisis basados en probabilidad son ampliamente utilizados para calcular las posibilidades de un equipo de ganar, basándose en el desempeño pasado, las condiciones climáticas o las estadísticas de los jugadores.

Gamificación de los Conceptos de Probabilidad

El atractivo de la probabilidad en el mundo real también se encuentra en los juegos:

Juegos de Cartas: El póker demuestra conceptos como eventos independientes (barajar las cartas) y probabilidades condicionadas (inferir las manos de otros jugadores basándose en las cartas repartidas).

Juegos de Mesa: El Monopoly implica la toma de decisiones estimando las probabilidades de caer en casillas específicas.

Juegos de Dados: En el Yahtzee, los jugadores estiman la probabilidad de obtener combinaciones como un trío.

Estos juegos no solo entretienen, sino que también ofrecen oportunidades de aprendizaje práctico, enseñándonos cómo las probabilidades se aplican al pensamiento estratégico.

Análisis de Distribuciones Comunes: Más Allá de la Probabilidad Básica

Las distribuciones de probabilidad ofrecen una visión más profunda sobre cómo se distribuyen los resultados en un rango de posibilidades. Vamos a explorar algunos tipos comunes que van más allá de lo básico:

Importancia de las Distribuciones de Probabilidad

Las distribuciones de probabilidad muestran cómo se asignan las probabilidades sobre los resultados de una variable aleatoria. Estos modelos nos permiten evaluar variadas condiciones y hacer predicciones en contextos complejos como psicología, física y finanzas.

Distribución Normal (Curva Gaussiana)

La distribución normal, comúnmente llamada curva de campana, es esencial en estadística debido a su simetría y comportamiento constante. Muestra que la mayoría de los puntos de datos se agruparán alrededor de la media, mientras que menos puntos de datos extremos aparecerán hacia los extremos.

Ejemplo: Las puntuaciones SAT siguen una distribución normal, con la mayoría de los estudiantes obteniendo calificaciones cercanas al promedio pero menos logrando puntajes muy altos o muy bajos. Si la puntuación media del SAT es 1050 con una desviación estándar de 100, aproximadamente el 68% de los estudiantes obtendrán puntajes entre 950 y 1150.

Distribución Binomial

La distribución binomial se centra en ensayos repetidos con dos resultados, como éxito y fracaso.

Ejemplo:

Lanzar una moneda 5 veces:

Éxito = "obtener cara."

Ensayos = 5 lanzamientos.

P(Cara) = 1/2.

La distribución binomial predice el número probable de éxitos en un conjunto de ensayos.

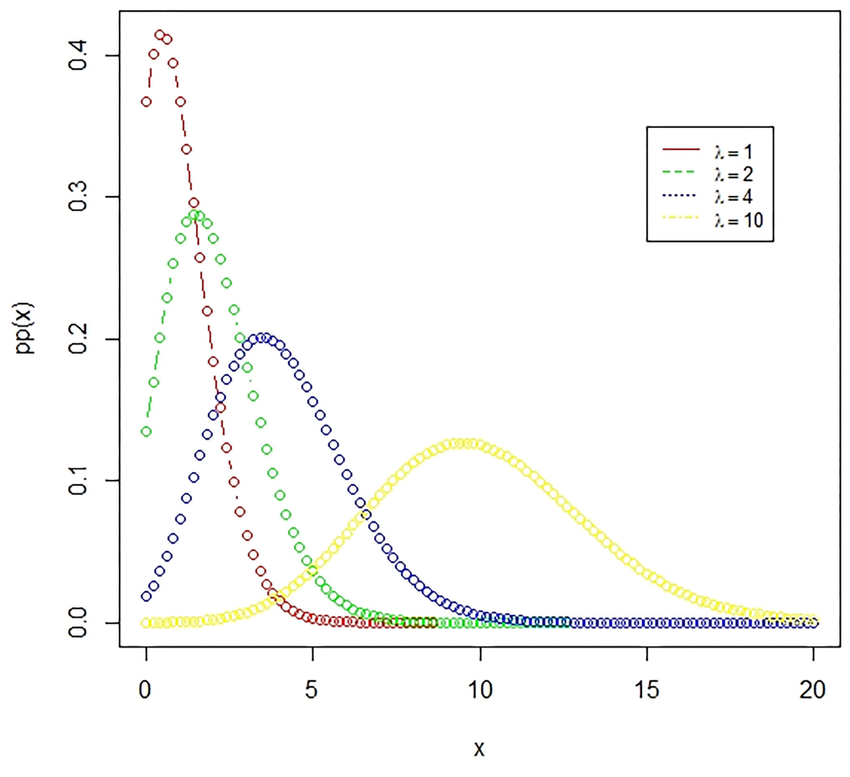
Distribución de Poisson

Las distribuciones de Poisson pueden usarse para modelar con qué frecuencia ocurre un evento en un intervalo de tiempo o espacio, por ejemplo, cuántos clientes llegan durante una hora basándose en tendencias históricas. Un restaurante podría usar la distribución de Poisson para predecir tales números de llegadas usando tendencias históricas como ejemplo.

Las distribuciones de probabilidad nos proporcionan herramientas invaluables para comprender sistemas complejos, brindándonos perspectivas que son invaluables para el análisis de datos, la gestión de riesgos y más.

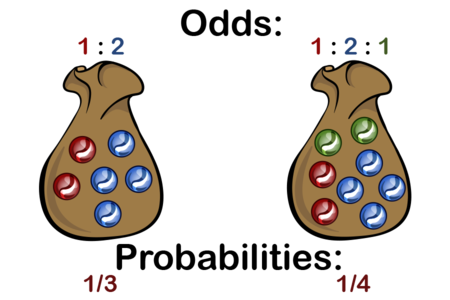
Tema Avanzado: Convertir Cuotas en Probabilidades

Entender la diferencia entre cuotas y probabilidades es fundamental para trabajar en áreas como las apuestas deportivas o el modelado estadístico, así que profundicemos y discutamos maneras de convertir entre ellas.

Cuotas vs. Probabilidades

Cuotas: Se expresan como una proporción de resultados favorables a resultados desfavorables.

Ejemplo: La probabilidad de sacar una canica específica es de 11:9 (11 favorables, 9 desfavorables).

Probabilidad: Se expresa como una fracción o porcentaje de resultados favorables en comparación con los resultados totales.

Conversión Paso a Paso

Escribir Cuotas como una Proporción

Para el ejemplo anterior, cuotas = 11:9. Esto significa:

Resultados favorables = 11.

Resultados desfavorables = 9.

Sumando Valores para Obtener Resultados Totales

Resultados totales = Favorables + Desfavorables = 11+9=20.

Aplicando la Fórmula de Probabilidad

P(Evento)=Resultados Favorables/Total de Resultados Posibles

Así que:

P(Evento)=\(\frac{11}{20}\)=0.55 o 55%.

Cálculos Inversos: De Probabilidades a Cuotas

¿Qué pasa si empiezas con una probabilidad y necesitas expresarla como cuotas? Invierte el proceso:

resta uno de tu valor de probabilidad para ver los resultados desfavorables;

convierte tu número de probabilidad en la proporción entre resultados favorables y desfavorables, etc.

Ejemplo: Si P(ganar)=0.4:

Probabilidad desfavorable =1−0.4=0.6.

Cuotas =4:6 o simplificado, 2:3.

Resolución Estratégica de Problemas con Probabilidad

Uno de los aspectos más importantes de la probabilidad es aprender a abordar problemas de manera sistemática, especialmente cuando se trata de escenarios complejos.

Reconociendo Tipos de Problemas

Los problemas de probabilidad suelen caer en categorías específicas:

Eventos únicos: Cálculos directos.

Eventos combinados: Uso de reglas de Y/O para múltiples eventos.

Probabilidad condicional: Ajuste de las probabilidades basado en un resultado inicial.

Ejemplo:

Te preguntan cuál es la probabilidad de sacar un rey rojo de un mazo de cartas barajadas. Reconocer esto como un problema de evento único te guiará inmediatamente a aplicar la fórmula fundamental:

P(Rey Rojo)=Resultados Favorables(2)/Resultados Posibles Totales(52)=\(\frac{1}{26}​.\)

Uso de Mapas de Probabilidad

Los Mapas de Probabilidad ofrecen un método innovador para resolver problemas de probabilidad organizando eventos y resultados en estructuras arbóreas, representando visualmente eventos con probabilidades asociadas y representando visualmente cómo se desarrollan los eventos a lo largo del tiempo.

Escenario: Una bolsa tiene 3 canicas rojas y 2 canicas azules. ¿Cuál es la probabilidad de sacar dos rojas sin reemplazo?

Sacar la primera roja: P=3/5.

Sacar la segunda roja: P=2/4.

¡Mapéalo!: Crea ramas para los resultados de rojo y azul para trazar los cálculos de manera intuitiva.

Errores Comunes en Probabilidad y Cómo Evitarlos

La probabilidad puede ser engañosamente complicada, y muchos estudiantes, tanto principiantes como experimentados, caen en trampas comunes. Esta sección destaca errores frecuentes y ofrece estrategias para evitarlos.

Errores al Sumar o Multiplicar Probabilidades

Uno de los errores más comunes es elegir incorrectamente entre las reglas de suma y multiplicación.

Trampa de la Regla de Suma:

Los estudiantes a menudo suman probabilidades cuando los eventos son independientes, por ejemplo, al lanzar cara dos veces.

Enfoque Correcto: La multiplicación se aplica aquí:P(Cara, luego Cara)=P(Cara)×P(Cara)=\(\frac{1}{2}×\frac{1}{2}=\frac{1}{4}​.\)

Uso Correcto de la Regla de Suma:

Suma probabilidades solo para eventos mutuamente excluyentes, por ejemplo, "¿Cuál es la probabilidad de sacar un 5 o un 6 en un dado?"

P(5 o 6)=P(5)+P(6)=\(\frac{1}{6}+\frac{1}{6}=\frac{2}{6}\).

Olvidar Ajustes de Probabilidad Condicional

Las probabilidades condicionales, especialmente en situaciones sin reemplazo, suelen confundir a los estudiantes.

Ejemplo: Seleccionar dos canicas rojas de una bolsa con 3 rojas y 2 azules sin reemplazo requiere recalcular los resultados totales para el segundo evento:

P(Segunda Roja | Primera Roja)=\(\frac{2}{4}​, no \frac{3}{5}\).

Solución: Representa visualmente el espacio muestral (por ejemplo, árboles de eventos) para tener en cuenta los totales cambiantes.

Malinterpretación de Cuotas y Probabilidades

Las cuotas y probabilidades son diferentes, pero muchos estudiantes las confunden. Por ejemplo, si las cuotas de ganar son 5:3 (5 resultados favorables por cada 3 desfavorables), la probabilidad sería:

P(Ganar)=\(\frac{5}{5+3}​=\frac{5}{8}​\),

no 5/3.

Verificación Durante la Resolución

Introduce el concepto de verificar tu solución trazando los cálculos hacia atrás.

Ejemplo: Si la probabilidad final de un evento no suma valores entre 0 y 1, retrocede en la lógica a través de suposiciones y fórmulas.

Al identificar estos obstáculos comunes y tomar medidas preventivas como usar herramientas, verificar con fórmulas, y dividir problemas en partes más pequeñas, puedes dominar incluso cálculos de probabilidad complejos con confianza.

Práctica y Ejercicios para Dominar la Probabilidad

Dominar la probabilidad se logra con práctica. Problemas que van desde cálculos simples hasta aplicaciones avanzadas ayudan a solidificar conceptos y mejorar las habilidades para resolver problemas.

Problemas Guiados Paso a Paso

Problema 1: Evento Simple

Escenario: Lanzas un dado de seis caras. ¿Cuál es la probabilidad de obtener un número mayor que 4?

Solución:

Resultados favorables: 5, 6 (2 resultados).

Resultados totales: {1, 2, 3, 4, 5, 6} = 6.P(Mayor que 4)=Resultados Favorables/Total de Resultados Posibles​=\(\frac{2}{6}​=\frac{1}{3}​\).

Problema 2: Eventos Combinados (Regla Y)

Escenario: Tiras una moneda y lanzas un dado. ¿Cuáles son las probabilidades de obtener cara en el lanzamiento de la moneda y un 3 en el dado de seis caras?

Solución:

P(Cara) = 1/2.

P(Obtener un 3) = 1/6.

Los eventos son independientes:

P(Cara Y 3)=P(Cara)×P(3)=\(\frac{1}{2}​​×\frac{1}{6}​=\frac{1}{12}\)​.

Conclusión

La probabilidad puede parecer intimidante al principio, pero una vez que se comprenden sus principios básicos, se convierte en un recurso invaluable, desde estimar las probabilidades de eventos simples hasta abordar situaciones complejas del mundo real con confianza y tomar decisiones informadas usando la probabilidad. Dividiendo los problemas en pasos manejables usando fórmulas o árboles de eventos para simplificar tu análisis, pronto te volverás experto en manejar incluso situaciones complejas con confianza.

La probabilidad se ha vuelto un componente integral de la vida cotidiana, desde la predicción de juegos y el análisis de datos, hasta tomar decisiones diarias, o simplemente entender mejor la probabilidad como parte de la vida en general. Con práctica y exposición en varios contextos, la probabilidad rápidamente se convierte en algo práctico que las personas usan intuitivamente, más que como una teoría matemática abstracta.

Dominar la probabilidad requiere más que resolver ecuaciones; se trata de desarrollar un enfoque para entender y navegar un mundo incierto. Con paciencia y práctica, cualquiera puede aprovechar el potencial para razonar críticamente y tomar decisiones seguras. ¡Feliz cálculo!

Referencia:

https://www.healthknowledge.org.uk/public-health-textbook/research-methods/1b-statistical-methods/statistical-distributions

https://www.linkedin.com/pulse/quantitative-risk-management-tools-techniques-monday-utomwen

https://www.researchgate.net/publication/375064637_The_Impact_of_Sample_Size_on_the_Probability_Samples_to_Estimate_the_Total_population_Number