¿Qué es la probabilidad?

La probabilidad impregna muchos aspectos de nuestra vida cotidiana, desde la predicción del clima hasta las probabilidades en los juegos. Pero, ¿qué es exactamente la probabilidad? ¿Representa alguna propiedad intrínseca de la realidad, o simplemente los humanos utilizan modelos mentales de incertidumbre como una forma de defensa contra el riesgo? En este artículo nos sumergimos profundamente en la probabilidad explorando su definición, fundamentos teóricos, desarrollo histórico y aplicaciones prácticas; nuestro objetivo es obtener una imagen completa de su importancia en diversos campos.

Definición

Conceptos Básicos

La probabilidad, en su definición básica, mide la probabilidad de que algo suceda y cuantifica la incertidumbre al proporcionar un valor numérico entre 0 y 1, donde 1 representa certeza y 0 representa imposibilidad. La probabilidad se apoya en gran medida en conceptos asociados con la aleatoriedad e incertidumbre inherentes tanto a procesos naturales como humanos.

Introducción a Términos Relacionados

Variable Aleatoria

Definición

Las variables aleatorias son componentes esenciales de la teoría de la probabilidad y la estadística, proporcionándonos diferentes valores numéricos dependiendo de los resultados de experimentos aleatorios. Hay dos categorías de variables aleatorias: discretas y continuas.

- Variable Aleatoria Discreta: Una variable aleatoria discreta tiene un conjunto finito o enumerable de valores distintos; ejemplos pueden incluir el número de caras en 10 lanzamientos de moneda, artículos defectuosos encontrados dentro de un lote o clientes entrando a una tienda dentro de una hora.

- Variable Aleatoria Continua: Las variables aleatorias continuas tienen la capacidad de asumir cualquier número de valores dentro de su rango especificado, como la altura de las personas o los tiempos dedicados a realizar tareas específicas, temperaturas en ciertos lugares.

Ejemplos

1. Variable Aleatoria Discreta: Considere lanzar un dado de seis caras. Los posibles resultados son 1, 2, 3, 4, 5 y 6. Si definimos una variable aleatoria \(X\) como el número mostrado en el dado, \(X\) es una variable aleatoria discreta porque solo puede tomar uno de seis valores específicos.

2. Variable Aleatoria Continua: Considere medir el tiempo que tarda una computadora en iniciar. Si definimos una variable aleatoria \(Y\) como el tiempo de inicio, \(Y\) es una variable aleatoria continua porque puede tomar cualquier valor dentro de un rango, como de 0 a 60 segundos.

Propiedades

- Función de Masa de Probabilidad (PMF): Para una variable aleatoria discreta, la función de masa de probabilidad \(P(X = x)\) da la probabilidad de que la variable aleatoria \(X\) tome el valor \(x\).

- Función de Densidad de Probabilidad (PDF): Para una variable aleatoria continua, la función de densidad de probabilidad \(f_Y(y)\) da la probabilidad relativa de que la variable aleatoria \(Y\) tome un valor específico \(y\). La probabilidad de que \(Y\) caiga dentro de un intervalo específico se encuentra integrando la PDF sobre ese intervalo.

- Función de Distribución Acumulativa (CDF): La función de distribución acumulativa \(F_X(x)\) para una variable aleatoria \(X\) da la probabilidad de que \(X\) sea menor o igual a \(x\). Para una variable aleatoria continua, es la integral de la PDF.

Distribución de Probabilidad

Definición

Las distribuciones de probabilidad proporcionan una descripción completa de cómo los valores de las variables aleatorias se distribuyen a lo largo del tiempo, desde variables aleatorias discretas con probabilidades discretas asociadas a cada valor posible hasta variables aleatorias continuas donde puede haber varios rangos posibles de probabilidades continuas dentro de sus rangos.

Tipos de Distribuciones de Probabilidad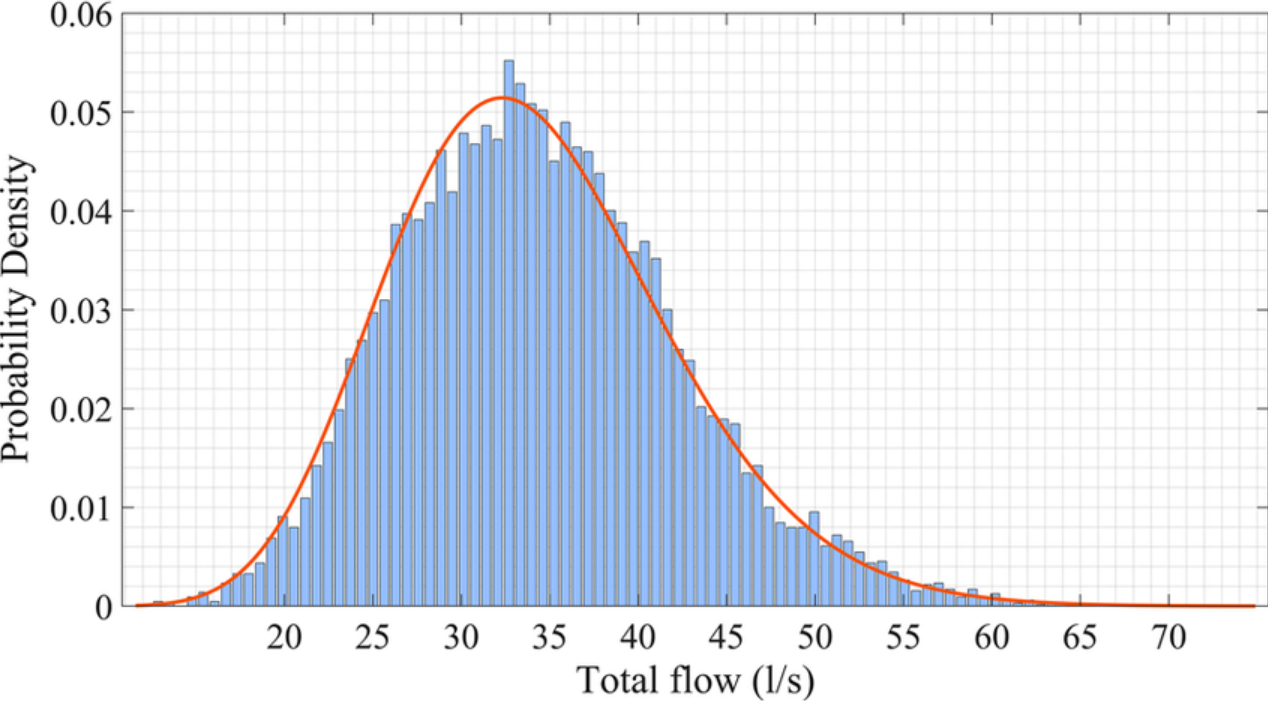

1. Distribuciones de Probabilidad Discretas:

- Distribución Binomial: Describe el número de éxitos en un número fijo de ensayos de Bernoulli independientes (por ejemplo, lanzar una moneda \(n\) veces).

- Distribución de Poisson: Describe el número de eventos que ocurren en un intervalo fijo de tiempo o espacio, dado un promedio constante (por ejemplo, el número de correos electrónicos recibidos por hora).

2. Distribuciones de Probabilidad Continuas:

- Distribución Normal: También conocida como la distribución Gaussiana, describe una variable aleatoria continua con una curva simétrica en forma de campana. Se caracteriza por su media (\(\mu\)) y desviación estándar (\(\sigma\)).

- Distribución Exponencial: Describe el tiempo entre eventos en un proceso de Poisson, donde los eventos ocurren de manera continua e independiente a una tasa constante.

Ejemplos

1. Distribución Binomial: Supongamos que lanzamos una moneda justa 10 veces. Sea \(X\) el número de caras obtenidas. \(X\) sigue una distribución binomial con parámetros \(n = 10\) y \(p = 0.5\).

2. Distribución Normal: Imagine que la población de hombres adultos está distribuida normalmente, con una altura media de 175 cm y una desviación estándar de 10 cm; entonces, cualquier adulto muestreado al azar de esta población sigue esta distribución cuando se mide su altura.

Valor Esperado

Definición

El valor esperado (o media) de una variable aleatoria es una medida del centro de su distribución. Representa el valor promedio de la variable aleatoria a lo largo de un número infinito de ensayos del experimento. El valor esperado se denota por \(E(X)\) para una variable aleatoria \(X\).

Cálculo

- Variable Aleatoria Discreta: El valor esperado \(E(X)\) de una variable aleatoria discreta \(X\) con posibles valores \(x_1, x_2, \ldots, x_n\) y probabilidades correspondientes \(P(X = x_i)\) se calcula como:

\(E(X) = \sum_{i=1}^{n} x_i \cdot P(X = x_i)\)

- Variable Aleatoria Continua: El valor esperado \(E(Y)\) de una variable aleatoria continua \(Y\) con función de densidad de probabilidad \(f_Y(y)\) se calcula como:

\(E(Y) = \int_{-\infty}^{\infty} y \cdot f_Y(y) \, dy\)

Ejemplos

1. Variable Aleatoria Discreta: Considere un dado con caras numeradas del 1 al 6. El valor esperado del resultado al lanzar el dado es:

\(E(X) = \sum_{i=1}^{6} i \cdot \frac{1}{6} = \frac{1 + 2 + 3 + 4 + 5 + 6}{6} = 3.5\)

2. Variable Aleatoria Continua: Considere una variable aleatoria continua \(Y\) que representa el tiempo (en horas) para completar una tarea, con una distribución exponencial con parámetro de tasa \(\lambda = 1\). El valor esperado es:

\(E(Y) = \int_{0}^{\infty} y \cdot \lambda e^{-\lambda y} \, dy = \frac{1}{\lambda} = 1 \text{ hora}\)

Varianza

Definición

La varianza es una medida de dispersión o variación entre los valores de una variable aleatoria y sus valores esperados, y cuantifica cuánto varían de ellos. La varianza de una variable aleatoria \(X\) se denota por \(\text{Var}(X)\).

Cálculo

- Variable Aleatoria Discreta: La varianza \(\text{Var}(X)\) de una variable aleatoria discreta \(X\) con valor esperado \(E(X)\) se calcula como:

\(\text{Var}(X) = E[(X - E(X))^2] = \sum_{i=1}^{n} (x_i - E(X))^2 \cdot P(X = x_i)\)

- Variable Aleatoria Continua: La varianza \(\text{Var}(Y)\) de una variable aleatoria continua \(Y\) con valor esperado \(E(Y)\) se calcula como:

\(\text{Var}(Y) = E[(Y - E(Y))^2] = \int_{-\infty}^{\infty} (y - E(Y))^2 \cdot f_Y(y) \, dy\)

Ejemplos

1. Variable Aleatoria Discreta: Considere el mismo ejemplo del dado. El valor esperado es 3.5. La varianza se calcula como:

\(\text{Var}(X) = \sum_{i=1}^{6} (i - 3.5)^2 \cdot \frac{1}{6} = \frac{1}{6}[(1 - 3.5)^2 + (2 - 3.5)^2 + \ldots + (6 - 3.5)^2] = 2.92\)

2. Variable Aleatoria Continua: Para el ejemplo de distribución exponencial con parámetro de tasa \(\lambda = 1\), la varianza es:

\(\text{Var}(Y) = \int_{0}^{\infty} (y - 1)^2 \cdot e^{-y} \, dy = 1\)

Si tienes alguna pregunta sobre estos ejemplos, puedes consultar a tutores en línea de UpStudy en Preguntar a Tutores.

Diagrama de Árbol de Probabilidad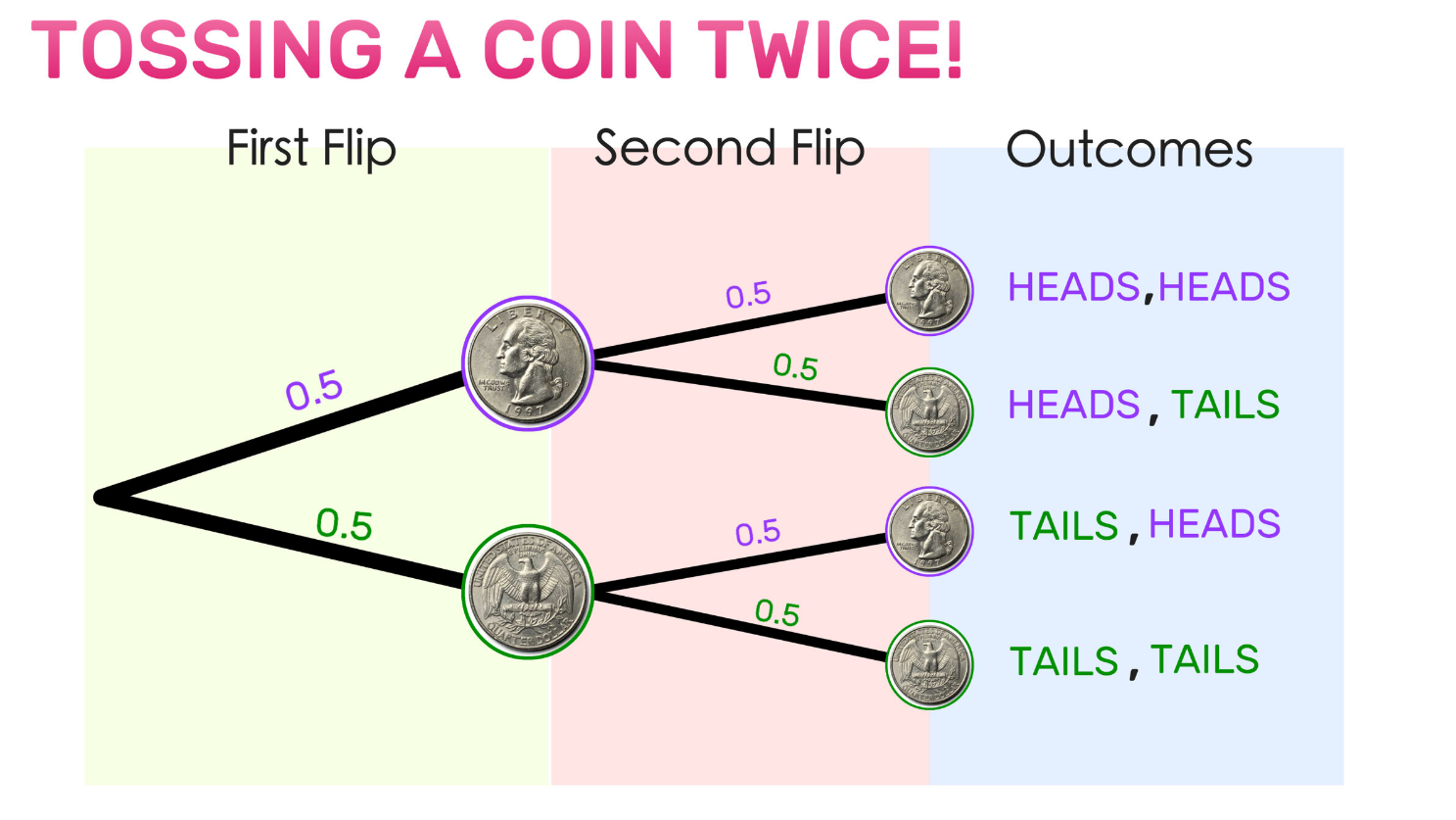

Los diagramas de árboles de probabilidad proporcionan una representación visual de todos los posibles resultados de un experimento y sus probabilidades asociadas, siendo especialmente útiles al manejar experimentos complejos con múltiples pasos o eventos. Cada rama en un árbol de probabilidad representa un resultado con probabilidades asociadas para ayudar a visualizar el espacio muestral y calcular probabilidades de eventos compuestos de manera más rápida y efectiva.

Considere, por ejemplo, un experimento en el que lanzamos una moneda y tiramos un dado; su diagrama de árbol de probabilidad consistiría en dos ramas iniciales para los lanzamientos de moneda (cara o cruz) seguidas de seis ramas adicionales que representan las tiradas de dado (1 al 6). Esto nos permite calcular fácilmente eventos combinados, como obtener cara primero antes de sacar 3! Este diagrama permite una predicción precisa.

Tipos

Las probabilidades pueden dividirse en varias clases dependiendo de cómo se determinan e interpretan; estas categorías incluyen probabilidades clásicas, empíricas y subjetivas.

Probabilidad Clásica

La probabilidad clásica (también conocida como probabilidad a priori o teórica) asume que todos los resultados en el espacio muestral son igualmente probables, calculada dividiendo el número de resultados favorables por todos los resultados posibles. Se aplica frecuentemente en juegos de azar como lanzar dados o sacar cartas donde las condiciones pueden ser bien controladas y entendidas.

Probabilidad Empírica

La probabilidad empírica, a menudo llamada probabilidad experimental o de frecuencia relativa, se basa en datos observados. Para estimar la probabilidad empírica con precisión, se debe realizar varias veces con resultados grabados después de cada prueba y se estima dividiendo el número de veces que ocurrió un evento por el total de pruebas completadas, un enfoque útil al tratar fenómenos del mundo real difíciles de medir con precisiones teóricas.

Probabilidad Subjetiva

La probabilidad subjetiva se basa más en juicio subjetivo u opinión que en datos objetivos al hacer predicciones de eventos como elecciones y ventas de productos, en lugar de en hechos y cifras sólidos. Las probabilidades subjetivas reflejan el grado de creencia de una persona sobre una ocurrencia y se emplean comúnmente cuando no hay suficientes datos empíricos disponibles o se necesitan predecir eventos únicos, como elecciones políticas o lanzamientos de ventas de nuevos productos.

Probabilidad Axiomática

La probabilidad axiomática ofrece una base matemática sólida para la teoría de probabilidad. Se basa en tres axiomas fundamentales: no negatividad, donde

Teoría de la Probabilidad

Definición

La teoría de la probabilidad es un área de las matemáticas que se ocupa de examinar fenómenos aleatorios. Proporciona un marco formal y herramientas necesarias para cuantificar y analizar la incertidumbre; en su núcleo, la teoría de la probabilidad explora variables aleatorias, procesos estocásticos, eventos y modelos matemáticos diseñados para representar probabilidades asociadas con varios resultados.

Terminología Relacionada

Para comprender completamente la teoría de la probabilidad, es esencial entender varios términos clave.

Experimento

Un experimento es cualquier proceso o acción que produce múltiples resultados, típicamente para investigación estadística o propósitos educativos. Los experimentos a menudo se repiten bajo condiciones similares para estudiar cómo se distribuyen los resultados a lo largo del tiempo; ejemplos incluyen lanzar un dado, lanzar monedas o realizar encuestas son considerados experimentos.

Espacio Muestral

El espacio muestral es el conjunto de todos los resultados posibles de un experimento. Representa el universo de todos los resultados potenciales. Por ejemplo, el espacio muestral para lanzar un dado de seis caras es {1, 2, 3, 4, 5, 6}.

Evento

Un evento es cualquier subconjunto del espacio muestral. Los eventos pueden ser simples (consistentes de solo un resultado) o compuestos (involucrando múltiples resultados). Un número par al lanzar dados (con resultados 2, 4, y 6 como resultados) calificaría como un evento compuesto.

Probabilidad (Definición en Teoría de la Probabilidad)

En teoría de la probabilidad, la probabilidad de un evento se define como la medida de la probabilidad de que el evento ocurra. Es un valor entre 0 y 1, inclusive, donde 0 indica que el evento no ocurrirá y 1 indica que el evento ciertamente ocurrirá. Matemáticamente, la probabilidad de un evento \(A\) se denota por \(P(A)\).

H4: Experimento Aleatorio

Experimentos aleatorios o procesos cuyos resultados no pueden predecirse con certeza incluyen lanzar dados, sacar cartas de mazos o medir temperaturas en ubicaciones específicas. Cada realización de tales pruebas se conoce como "pruebas," mientras sus resultados permanecen impredecibles. Ejemplos pueden incluir lanzar un dado, sacar de mazos de cartas o medir la temperatura en lugares específicos.

Teoremas de Probabilidad

La teoría de la probabilidad se basa en varios teoremas fundamentales que proporcionan reglas para calcular probabilidades, haciendo de este campo una parte integral en la resolución de problemas complejos de probabilidad y en comprender el comportamiento de variables aleatorias.

Cálculos de Probabilidad Simple

Los cálculos de probabilidad simple implican determinar la probabilidad de eventos individuales o combinaciones de eventos basados en principios fundamentales de probabilidad, incluidas las reglas de adición y multiplicación.

Regla de la Adición

La regla de la adición se utiliza para calcular la probabilidad de la unión de dos eventos. Para dos eventos mutuamente excluyentes \(A\) y \(B\), la probabilidad de que ocurra ya sea \(A\) o \(B\) se da por:

\[P(A \cup B) = P(A) + P(B)\]

Si los eventos no son mutuamente excluyentes, la fórmula se ajusta para tener en cuenta la superposición:

\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

H5: Regla de la Multiplicación

La regla de la multiplicación se utiliza para calcular la probabilidad de la intersección de dos eventos. Para dos eventos independientes \(A\) y \(B\), la probabilidad de que ambos \(A\) y \(B\) ocurran se da por:

\[P(A \cap B) = P(A) \times P(B)\]

Si los eventos no son independientes, la fórmula se ajusta para tener en cuenta la probabilidad condicional:

\[P(A \cap B) = P(A) \times P(B|A)\]Fórmula de Probabilidad Total

La fórmula de probabilidad total se utiliza para calcular la probabilidad de un evento basado en las probabilidades de eventos relacionados. Es particularmente útil al tratar con probabilidades condicionales y se da por:

\[P(B) = \sum_{i=1}^{n} P(B|A_i) \times P(A_i)\]

donde \(A_1, A_2, \ldots, A_n\) son eventos mutuamente excluyentes y exhaustivos.

Teorema de Bayes

El teorema de Bayes es un resultado fundamental en teoría de la probabilidad que relaciona probabilidades condicionales. Proporciona una manera de actualizar la probabilidad de un evento basado en nueva evidencia y se da por:

\[P(A|B) = \frac{P(B|A) \times P(A)}{P(B)}\]

El teorema de Bayes se utiliza ampliamente en varios campos, incluyendo estadísticas, aprendizaje automático y teoría de decisiones, para hacer inferencias y actualizar creencias basadas en datos observados.

Si deseas intentar aplicar estas fórmulas, puedes encontrar problemas de ejemplo en la Banco de Estudio en UpStudy.

Historia de la Investigación de la Probabilidad

Los Comienzos en el Juego

Las raíces de la teoría de la probabilidad se pueden rastrear hasta el juego y los juegos de azar. A partir de los siglos XVI y XVII, los jugadores y matemáticos exploraron las reglas de los eventos aleatorios con el objetivo de aumentar sus probabilidades. Este período presenció el desarrollo temprano de la teoría de la probabilidad con contribuciones notables de figuras como Gerolamo Cardano y Blaise Pascal, entre muchos otros.

Siglos XVI y XVII

Trabajo Fundacional

Gerolamo Cardano fue un matemático, médico y jugador italiano reconocido por su trabajo pionero en la teoría de la probabilidad. En su libro de 1560, Liber de Ludo Aleae (El Libro de los Juegos de Azar), escrito durante esa época y publicado póstumamente en 1663, titulado El Libro de los Juegos de Azar, discutió principios básicos de probabilidad así como métodos para calcular probabilidades en varios juegos.

Blaise Pascal y Pierre de Fermat, dos prominentes matemáticos franceses, avanzaron más en las matemáticas durante mediados del siglo XVII. Su correspondencia sobre un problema de juego llamado Los Puntos (que involucra la división justa de las apuestas en un juego interrumpido) sentó un camino hacia la teoría moderna de la probabilidad a través de los modelos de valor esperado que desarrollaron; su trabajo finalmente sentó las bases de los estudios modernos de probabilidad.

H4: Teoría de Errores

A finales del siglo XVII, la teoría de errores se convirtió en un tema influyente dentro de los estudios de probabilidad. Pioneros como Isaac Newton y Edmond Halley trataron de medir los errores así como su distribución en las mediciones. La teoría de errores jugó una parte esencial en la creación de métodos estadísticos así como en la aplicación de la probabilidad a las observaciones científicas.

Siglos XIX y XX

Método de los Mínimos Cuadrados

En el siglo XIX, la teoría de la probabilidad y la estadística vieron avances significativos. Carl Friedrich Gauss (un matemático alemán) introdujo el método de los mínimos cuadrados de Carl, que minimiza la suma de las diferencias de cuadrados entre valores observados y predichos aplicando el método de los mínimos cuadrados de Carl Friedrich Gauss, una técnica importante relacionada con la teoría de errores que más tarde se convirtió en una parte central del análisis estadístico y los modelos de regresión.

Teorema del Límite Central

El Teorema del Límite Central (TLC), uno de los resultados clave en la teoría de la probabilidad, se desarrolló por primera vez entre 1881 y 1920. Según este teorema, cuando se toman en conjunto, múltiples variables aleatorias independientes y distribuidas aleatoriamente se acercan a una distribución normal a cualquier nivel en su distribución total de suma, independientemente de cómo estuvieran originalmente distribuidas, su suma (o distribución promedio) eventualmente se parecerá a esta distribución de curva normal resultante de la inferencia estadística o el análisis de fenómenos aleatorios. Tiene aplicaciones de gran alcance.

La teoría de la probabilidad continuó su progreso durante el siglo XX gracias a las contribuciones de matemáticos como Andrey Kolmogorov, quien formalizó sus fundamentos axiomáticos, y Paul Lévy, quien hizo avances significativos en la investigación de procesos estocásticos. Tales desarrollos cimentaron el lugar de la teoría de la probabilidad como una rama esencial de las matemáticas con numerosas aplicaciones en ciencia, ingeniería, economía y más allá.

Aplicaciones de la Probabilidad

Aplicaciones en Ciencias Teóricas

La teoría de la probabilidad juega un papel crucial en varias ciencias teóricas, proporcionando el marco matemático para modelar y analizar fenómenos aleatorios.

Física

La probabilidad desempeña un papel indispensable en la comprensión y predicción del comportamiento de los sistemas tanto a nivel macroscópico como microscópico, incluida la mecánica cuántica que depende en gran medida de las probabilidades para describir el comportamiento de las partículas; su naturaleza probabilística se puede capturar dentro de su función de onda que describe las probabilidades asociadas con encontrar partículas en varios estados de movimiento.

Ciencias Biomédicas

La probabilidad se puede usar en ciencias biomédicas para estudiar la efectividad de los tratamientos, la propagación de enfermedades y los patrones de herencia genética. Los ensayos clínicos que dependen en gran medida de métodos estadísticos derivados de la teoría de probabilidad emplean técnicas estadísticas derivadas de ella para probar la eficacia de nuevos medicamentos, mientras que los epidemiólogos utilizan modelos de probabilidad para rastrear la dinámica de transmisión de enfermedades infecciosas y predecir brotes.

Informática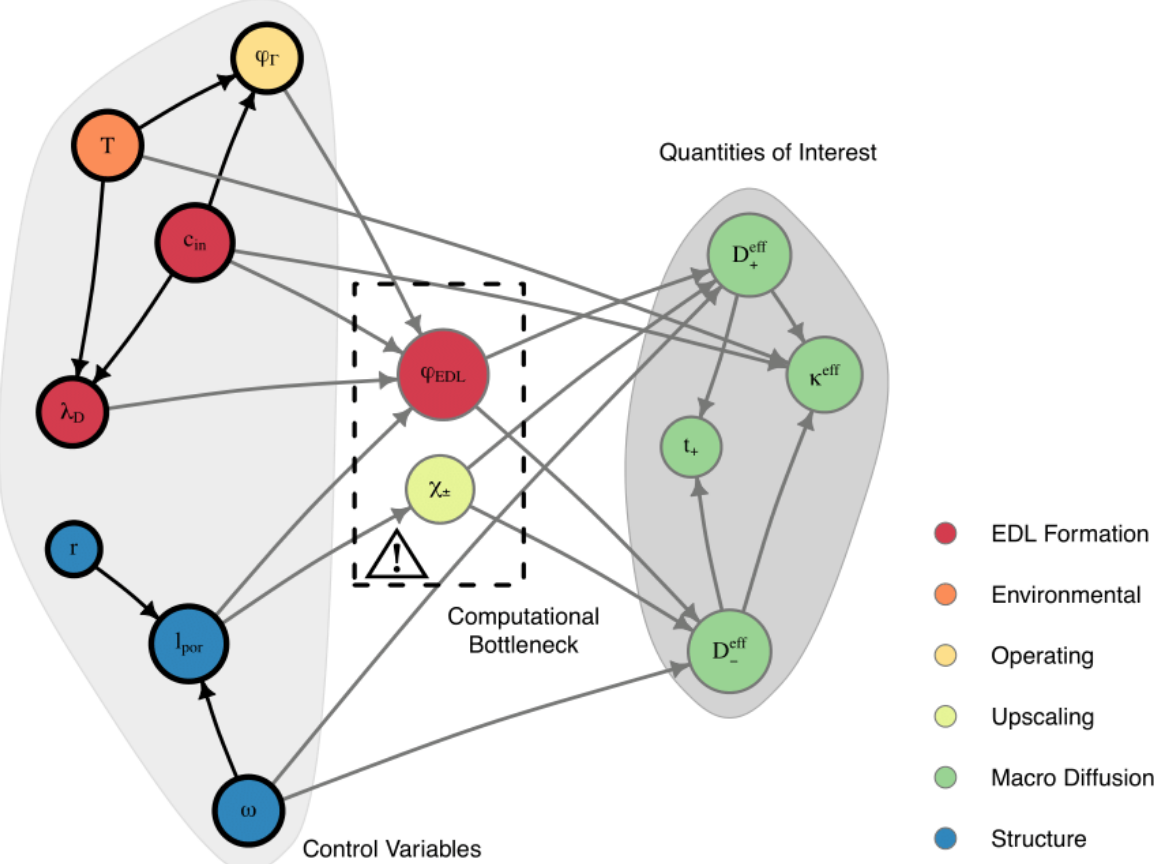

La probabilidad está en el núcleo de la informática, particularmente en áreas como el aprendizaje automático, la inteligencia artificial y los algoritmos. Los modelos y métodos probabilísticos se emplean en el desarrollo de algoritmos capaces de aprender de conjuntos de datos, hacer predicciones con información limitada o manejar la incertidumbre de manera efectiva. Las redes bayesianas—un ejemplo de un modelo gráfico probabilístico usado para el razonamiento bajo incertidumbre—sirven esta función efectivamente.

Ciencias Sociales

La probabilidad se ha convertido en una herramienta indispensable en la investigación de las ciencias sociales para estudiar el comportamiento humano, las interacciones sociales y los fenómenos económicos. Las encuestas, experimentos y estudios observacionales utilizan técnicas estadísticas derivadas de la teoría de probabilidad para analizar datos sobre poblaciones, mientras que los economistas utilizan modelos de probabilidad para estudiar el comportamiento del mercado, como el riesgo y la toma de decisiones bajo incertidumbre.

Aplicaciones en la Vida Real

La probabilidad no es simplemente un concepto abstracto: sus aplicaciones se extienden ampliamente en la vida cotidiana.

Aplicaciones en Meteorología

La probabilidad ha sido utilizada durante mucho tiempo en meteorología para predecir condiciones meteorológicas y eventos extremos como huracanes y tornados, usando modelos probabilísticos que analizan datos meteorológicos históricos, generan pronósticos que reflejan la incertidumbre de los procesos atmosféricos y ayudan a individuos y organizaciones a tomar decisiones informadas sobre actividades o medidas de seguridad.

Aplicaciones en Finanzas

La probabilidad juega un papel esencial en las finanzas al ayudar a modelar y mitigar el riesgo, analizar oportunidades de inversión y valorar derivados financieros. Los modelos probabilísticos como Black-Scholes se usan para estimar valores justos de opciones y otros instrumentos financieros mientras que los gestores de riesgos emplean métodos de análisis como Valor en Riesgo para medir las exposiciones de los portafolios al riesgo y evaluarlas y reducirlas en consecuencia.

Juegos y Apuestas

La probabilidad juega un papel integral en los juegos y las apuestas, donde se usa para calcular probabilidades, crear estrategias y evaluar la equidad de los juegos. Comprender la probabilidad ayuda a los jugadores a tomar decisiones informadas y gestionar los riesgos de manera más efectiva; los casinos usan modelos de probabilidad para crear juegos que sean tanto entretenidos como rentables.

Referencia:

1. https://en.wikipedia.org/wiki/Probability

2. https://en.wikipedia.org/wiki/Probability_theory